Modelagem e previsão com o {modeltime}
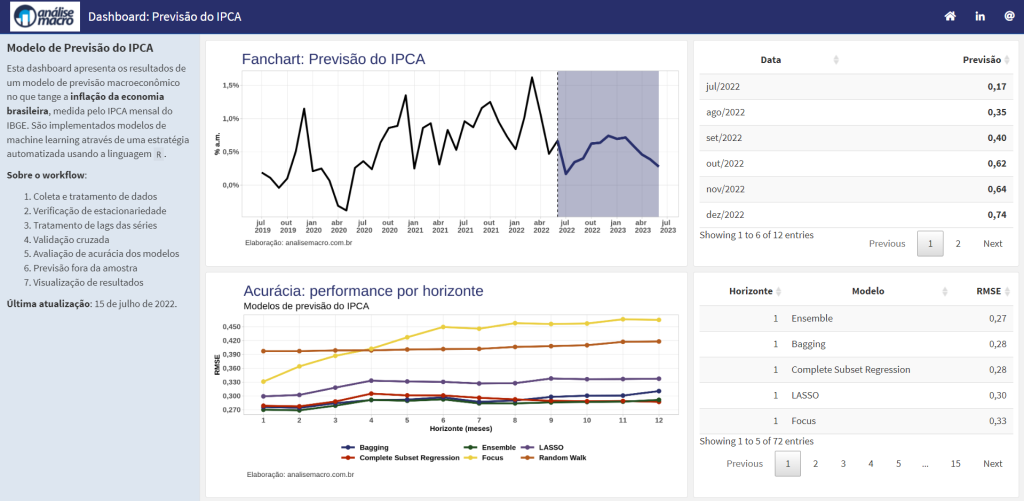
O pacote {modeltime} é um framework para modelagem e previsão de séries temporais no R, com a possibilidade de integração com o ecossistema do {tidymodels} para uso de técnicas de machine learning. O pacote promete ser uma interface veloz e moderna que possibilita prever séries temporais em grande escala (i.e. 10+ mil séries). Utilizando uma interface […]
Modelos ARIMA na abordagem bayesiana
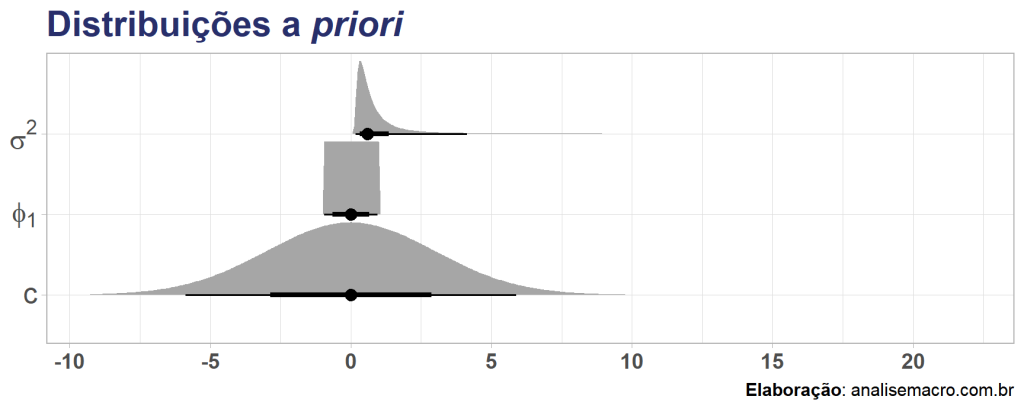
A boa e velha econometria nos proporciona métodos que são ótimos para relacionar variáveis e construir previsões, sendo quase sempre o primeiro ponto de partida para praticantes, além de ser a base de grande parte dos modelos "famosos" da atualidade. Como exemplo, em problemas de previsão de séries temporais a família de modelos ARIMA, popularizada […]
O ovo ou a galinha? Teste de causalidade de Granger na granja
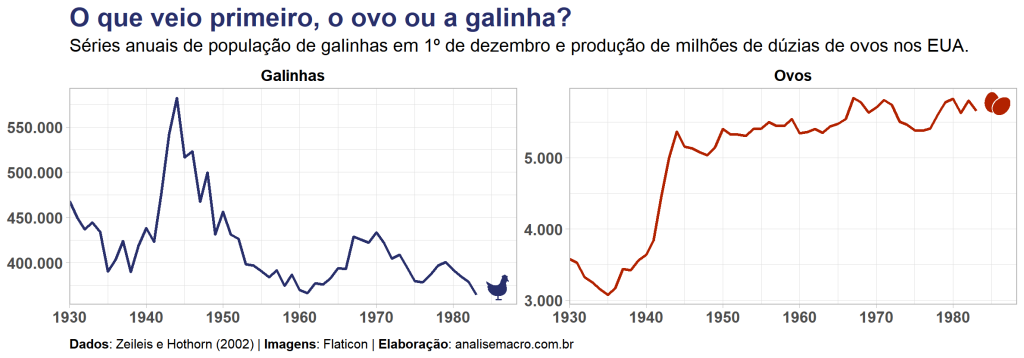
O ovo ou a galinha é uma referência a um dilema clássico de causalidade que comumente surge da pergunta "O que veio primeiro, o ovo ou a galinha?" O dilema parte da observação de que a galinha nasce do ovo e o ovo é colocado pela galinha, de modo que seria difícil determinar a sequência […]
Text mining dos comunicados do FOMC: prevendo mudanças na política
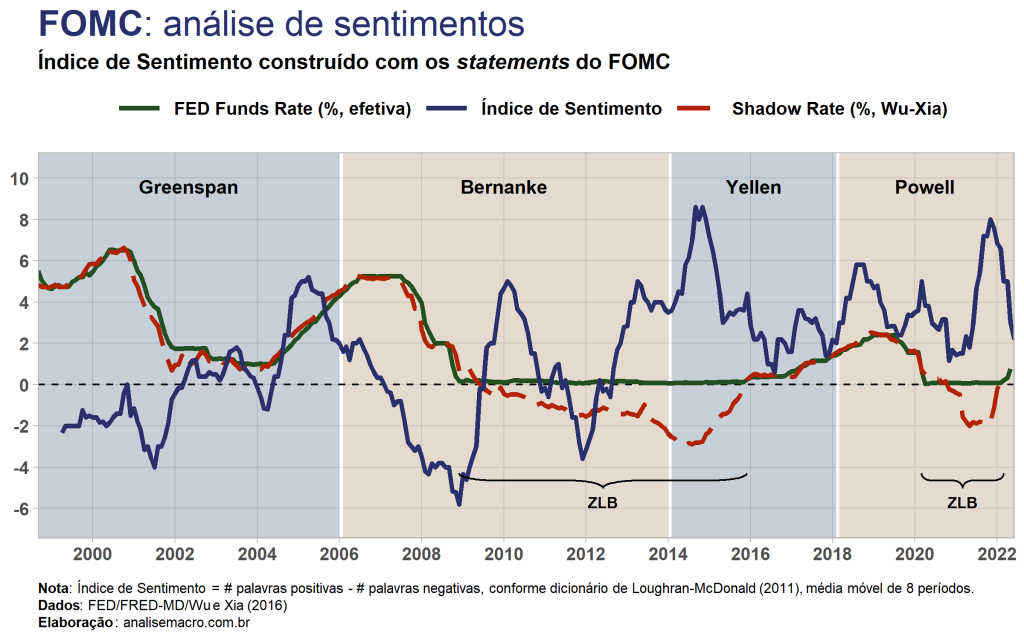
Neste exercício utilizaremos os statements do FOMC/FED para construir um índice de sentimentos, que busca quantificar sentimentos (i.e. positivo, negativo) através de informações textuais extraídas por técnicas de text mining. Em seguida, comparamos o índice com o principal instrumento de política monetária, a taxa de juros, e avaliamos sua utilidade em prever mudanças de política através do teste […]
Previsão da inflação (EUA) com fatores textuais do FOMC

Reflexo da era da informação, atualmente não se faz mais política monetária sem uma boa dose de comunicados, atas, entrevistas, conferências, etc. Os chamados central bankers atuam, sobretudo, como comunicadores e qualquer pequena nuance em sua comunicação (futuros passos da política monetária) pode ser um sinal para alvoroço nos "mercados". Nesse sentido, uma área da literatura econômica […]

