Do Zero à Previsão Macroeconômica: como começar?
Começamos nesse post, uma sequência de publicações que buscará mostrar como é possível construir previsões quantitativas de variáveis macroeconômicas. Ao longo das próximas semanas, buscaremos elucidar uma série de questões que surge nessa jornada, bem como mostrar ao leitor as possíveis soluções para esses problemas. Em particular, por onde começar? Antes de mais nada, leitor, […]
Modelos SARIMA
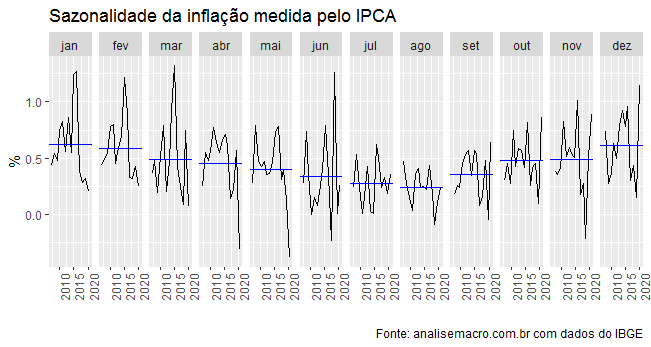
Modelos SARIMA são modelos da classe de modelos univariados de séries temporais. O acrônimo SARIMA significa modelos AutoRegressivos Integrados de Médias Móveis com Sazonalidade. São modelos bastante úteis para gerar previsão de séries temporais quando, em geral, não estão disponíveis variáveis preditoras. O aspecto mais interessante desse tipo de abordagem é justamente colocar a parte sazonal da […]
Medindo o efeito das Commodities sobre a inflação brasileira
O período da pandemia tem sido marcado por diversos choques que têm afetado a economia mundial. Em particular, o mundo assiste a um avanço bastante forte nos preços das commodities, inclusive as da área de energia, que são utilizadas como insumo em diversas cadeias produtivas. Um dos efeitos mais nítidos desse aumento nas commodities é […]
Evolução dos preços de combustíveis no Brasil
No Comentário de Conjuntura da semana passada, chamei atenção para a relação entre o preço do petróleo no mercado internacional e o preço da gasolina aqui no Brasil. Em particular, mostrei que as séries de petróleo, seja o tipo Brent, seja o WTI, são séries bastante voláteis ao longo do tempo. Dada a paridade adotada pela Petrobras desde 2016, […]
Cursos Aplicados de R e Python: Turmas de Outono
Abrimos hoje, 22/3, as inscrições com 30% de desconto para as Turmas de Outono dos nossos Cursos Aplicados de R e Python. As vagas com esse desconto são limitadas aos primeiros inscritos. Haverá vagas para 25 Cursos Livres e 3 Formações. As turmas de Outono terão início no dia 04/04 e contarão com Cursos de […]

