Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

A aprendizagem por transferência (transfer learning) é o reuso de um modelo pré-treinado em um novo problema. Portanto, sua utilização torna-se um avanço enorme para a previsão de diferentes tipos de variáveis, principalmente para aquelas ordenadas no tempo. Mostramos nesta postagem o uso do Transfer Learning com o Python para o caso de Séries Temporais.
Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel
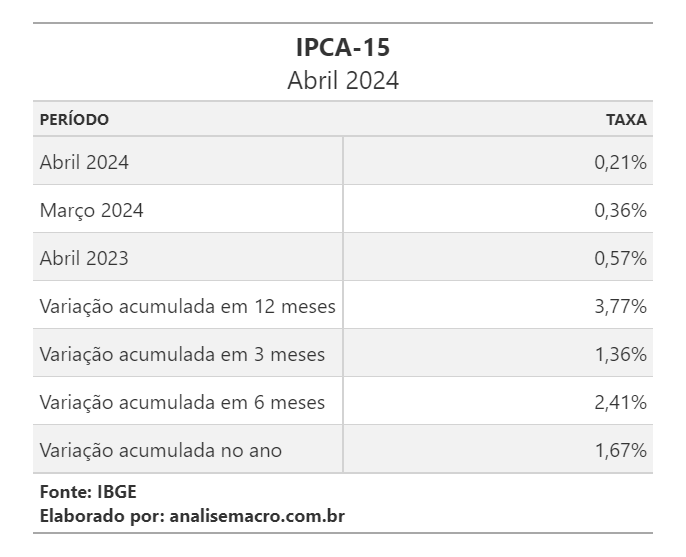
Nos dias atuais, pessoas que trabalham com dados estão constantemente confrontados com um dilema: criar uma tabela não tão genial no Excel ou manter em um formato ainda pior, como um dataframe, mas mantendo a flexibilidade de obtenção dos dados. Podemos resolver esse grande problema, unindo a flexibilidade e beleza ao usar a biblioteca great_tables do Python.
Análise do Censo Demográfico com o R
Como podemos analisar dados do Censo Demográfico para produzir pesquisas e implementar políticas públicas? Mostramos nesta postagem o resultado de uma breve análise dos dados preliminares do Censo Demográfico de 2022 usando o R.
Criando um Dashboard de análise de Ações no Python
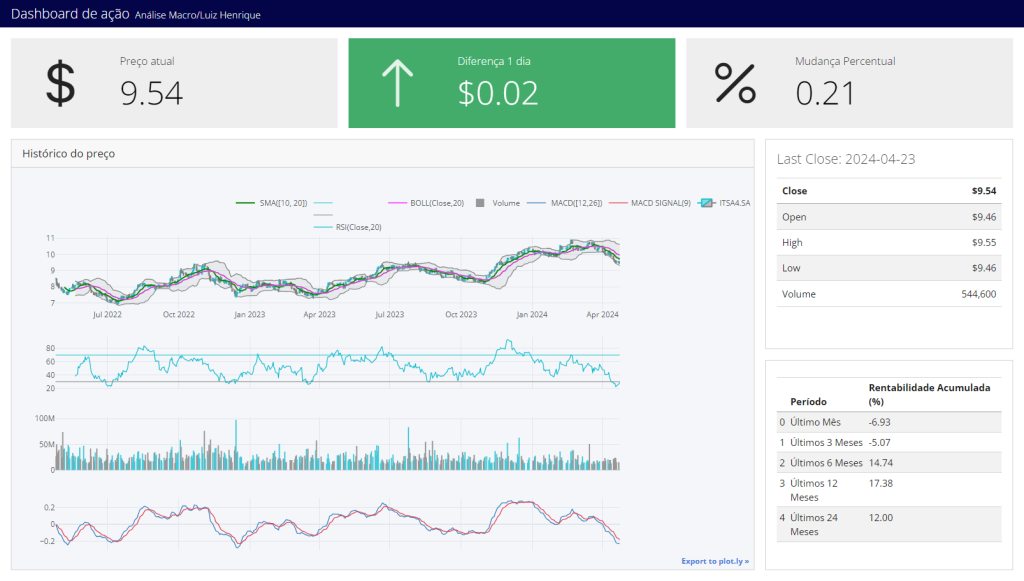
Um Dashboard é um painel de controle que consolida uma variedade de informações sobre um determinado objeto de estudo em um ou mais painéis. Ele simplifica significativamente o processo de análise de dados, oferecendo uma visão global e fácil de entender. Uma maneira simples de construir um Dashboard para acompanhar uma ação específica é utilizando duas ferramentas: Quarto e Python. Neste post, mostramos o resultado da criação de um Dashboard de Ação.
Analisando séries temporais no Python e esquecendo de vez o Excel
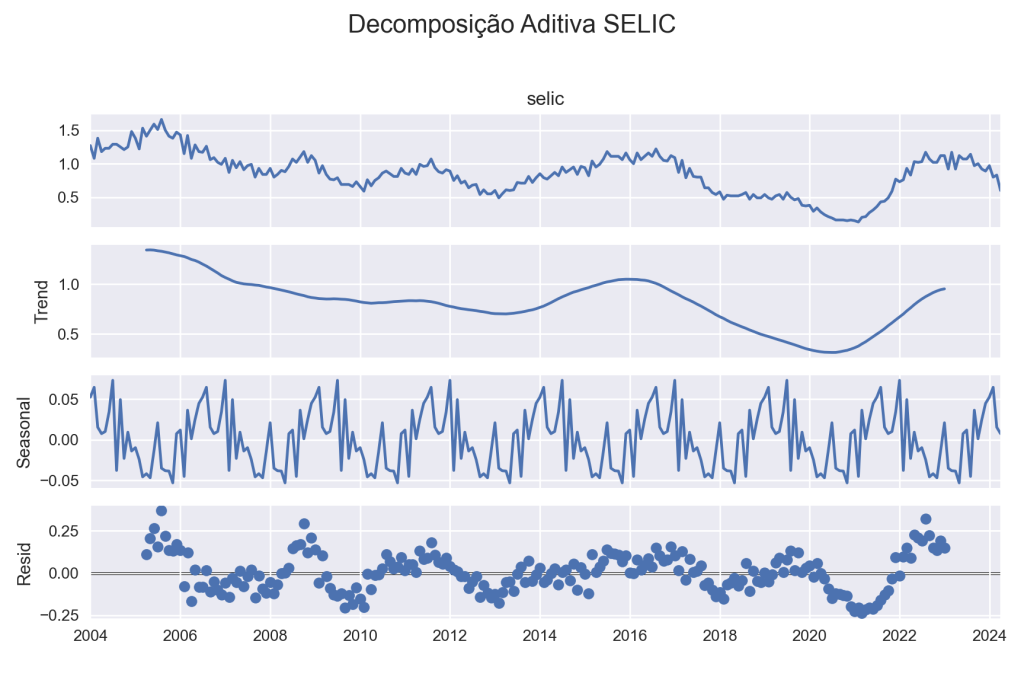
Séries temporais representam uma disciplina extremamente importante em diversas áreas, principalmente na economia e na ciência de dados. Mas, afinal, como lidar com esses dados que se apresentam ao longo do tempo? Neste exercício, demonstraremos como compreender uma série temporal e como o Python se destaca como uma das melhores ferramentas para analisar esse tipo de dado.

