O que é uma Série Temporal?
Dados de séries temporais (time series, no inglês) são estruturas de dados tabulares compostos de observações indexadas no tempo, frequentemente constituindo observações sequenciais e igualmente espaçadas entre períodos diferentes. A frequência de dados podem ser dispostas a hora, dia, semana, mensal, trimestral ou anual.
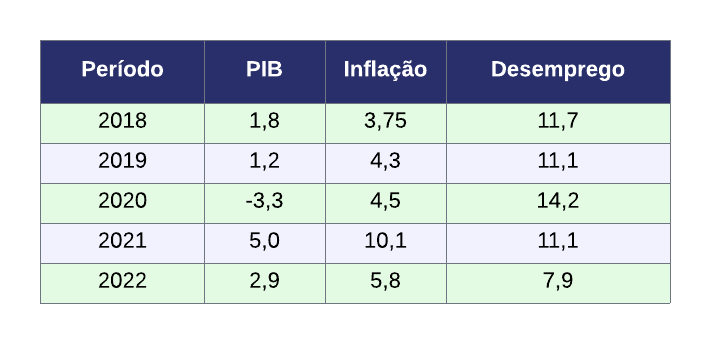
Diferente de dados de corte transversal (cross section, no inglês) são estruturas de dados tabulares que são coletados em apenas um período no tempo, podendo ser sobre diversas observações (como pessoas, empresas, países, etc.), dados com séries temporais, em linhas gerais, possuem um formato parecido com esse abaixo:
É uma estrutura de dados muito utilizada em diversas áreas como estatística, econometria, clima, finanças, macroeconomia e outras. A análise e a previsão de séries temporais são as aplicações mais comuns com essa estrutura de dados.
Aprenda a coletar, processar e analisar dados na formação de Do Zero à Análise de Dados com Python.
Para o nosso interesse, há diversos conjuntos de dados econômicos que se apresentam como uma série temporal, tais como:
- Taxa de desemprego;
- Juros básicos de uma economia;
- Produto Interno Bruto (PIB);
- Taxa de inflação.
Objetivos da análise de séries temporais
Conforme Morettin (2006), se temos em mãos uma série temporal , observada nos instantes
, estamos interessados em:
- Investigar o mecanismo gerador da série temporal;
- Descrever o comportamento passado da série, por meio de suas propriedades estatísticas e gráficos;
- Fazer previsões de valores futuros da série.
Para descrever as séries, modelos probabilísticos ou modelos estocásticos são construídos, e que no qual devem ser simples e parcimoniosos, isto é, devem ser fáceis de serem manipulados e devem possuir o menor número de parâmetros possível.
Decomposição de uma série temporal
De modo a compreender o processo gerador de dados de uma determinada série temporal, pode ser interessante decompô-la em alguns componentes, como abaixo:
(1)
Onde, no tempo ,
é uma série temporal,
é uma tendência,
é um efeito sazonal e
é um termo de erro.
Alternativamente, temos a decomposição multiplicativa:
(2)
A decomposição aditiva é a mais adequada se a magnitude das flutuações sazonais, ou a variação em torno do ciclo de tendência, não varia com o nível da série temporal.
Quando a variação no padrão sazonal, ou a variação em torno do ciclo de tendência, parece ser proporcional ao nível da série temporal, então uma decomposição multiplicativa é mais apropriada. Decomposições multiplicativas são comuns em séries temporais econômicas.
Componentes
Tendência
Uma tendência existe quando há um aumento ou diminuição de longo prazo nos dados. Não precisa ser linear. Às vezes, nos referiremos a uma tendência como “mudança de direção”, quando ela pode passar de uma tendência crescente para uma tendência decrescente.
Sazonalidade
Um padrão sazonal ocorre quando uma série temporal é afetada por fatores sazonais, como a época do ano ou o dia da semana. A sazonalidade é sempre de um período fixo e conhecido.
Ciclo e o Termo de erro
Um ciclo ocorre quando os dados exibem aumentos e quedas que não são de uma frequência fixa. Essas flutuações geralmente são devidas a condições econômicas e geralmente estão relacionadas ao “ciclo de negócios”. A duração dessas flutuações é geralmente de pelo menos 2 anos.
Quando decompomos uma série temporal em componentes, geralmente combinamos a tendência e o ciclo em um único componente de ciclo de tendência (geralmente chamado apenas de tendência para simplificar).
Assim, podemos pensar em uma série temporal como compreendendo três componentes: um componente de ciclo de tendência, um componente sazonal e um componente restante/termo de erro (contendo qualquer outra coisa na série temporal).
Pontos importantes:
Para algumas séries temporais (por exemplo, aquelas que são observadas pelo menos diariamente), pode haver mais de um componente sazonal, correspondendo aos diferentes períodos sazonais.
Análise de Séries Temporais
A análise de séries temporais é um conjunto de métodos e ferramentas que o analista utiliza para compreender o processo gerador de dados, permitindo compreender o comportamento de diversas variáveis. Permite também solidificar uma base para criar hipóteses e modelos preditivos/causais.
É importante saber que séries temporais são tipos de dados que possuem características únicas, portanto, é necessário entender alguns pontos, tanto por questões de análise, quanto também por questões de modelagem.
- Sazonalidade;
- Tendência;
- Autocorrelação;
- Estacionariedade.
Esses pontos podem ser analisados por meio de estatísticas e gráficos, entre eles
- Gráfico de linha;
- Média, mediana, desvio padrão e IQR;
- Gráfico de histograma;
- Gráfico de sazonalidade;
- Decomposição
- Correlogramas ACF e PACF;
Existem diversas outras características, bem como diversas ferramentas que podem ser analisadas em uma série econômica temporal, entretanto, as listadas acima são suficiente para gerar insights preciosos sobre a base de dados. Agora que entendemos o contexto e os pontos principais, vamos analisar duas séries econômicas reais: os dados do Índice Nacional de Preços ao Consumidor Amplo (IPCA) - % a.m. e Taxa de juros SELIC, efetiva, acum. no mês - % a.m..
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
As séries foram capturadas direto do Sistema Gerenciador de Séries Temporais usando a biblitoeca python-bcb, com ambas iniciando no ínicio de 2004.
Gráfico de Linha
O gráfico de linha, em que no eixo x é representado a data, e no eixo y os valores das séries, permite analisar e tirar conclusões de grande parte não somente do comportamento da série em si, como também de suas características estatísticas.
É possível avaliar o comportamento passado da série, analisar o que ocorreu e o que pode ocorrer, bem como realizar comparações com outras séries. Além disso, é possível avaliar os componentes (tendências e sazonalidade) da série e se possui um comportamento estacionario.
Estatística Descritiva
A estatística descritiva dispõe informações sobre a média, o desvio padrão e os percentis da série, ou seja, permite avaliar distribuição dos dados.
Código
ipca
count 243.000000
mean 0.464691
std 0.329469
min -0.680000
25% 0.250000
50% 0.440000
75% 0.640000
max 1.620000Código
selic
count 244.000000
mean 0.852090
std 0.314897
min 0.130000
25% 0.632500
50% 0.870000
75% 1.070000
max 1.660000Histograma
O Histograma permite avaliar a distribuição de dados das variáveis, demonstrando a frequência de ocorrência de cada valor da série.
Sazonalidade
A Sazonalidade refere-se a períodos fixos em determinada frequência em que há um aumento ou decréscimo do valor da variável. É muito comum encontrar sazonalidade em séries econômicas e financeiras. Exemplo: aumento de vendas de sorvete no verão e queda no inverno.
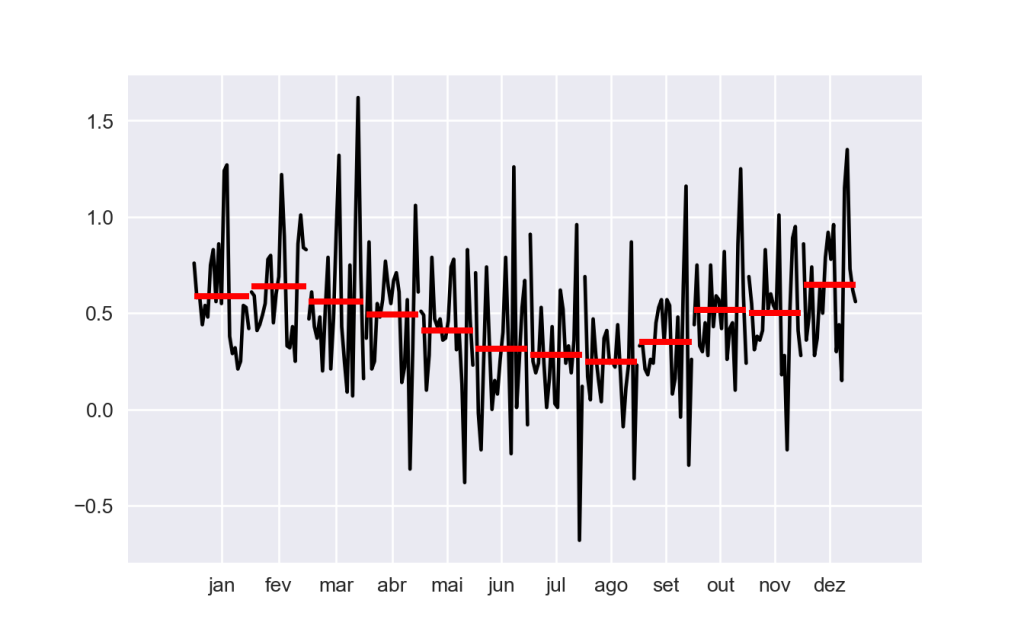
No IPCA é possível verificar a sazonalidade de algumas formas, um meio é avaliando o gráfico de série temporal (em algumas séries é bem evidente o comportamento de sazonalidade no gráfico); outro pode ser pelo cálculo da média do mês de todos os anos e comparar com os demais, como no gráfico abaixo.
Sazonalidade IPCA
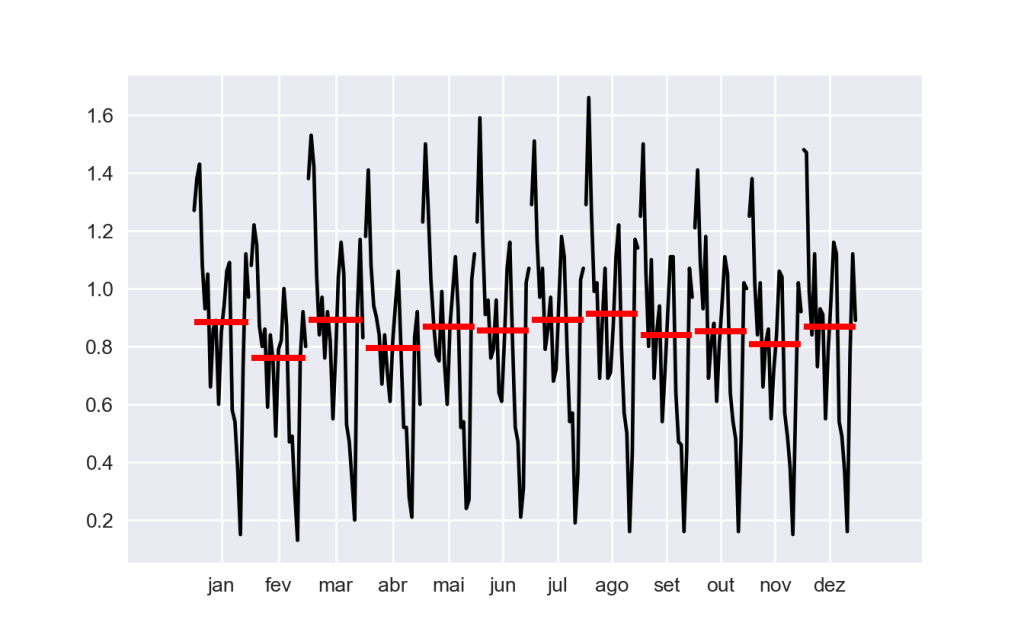
Sazonalidade SELIC
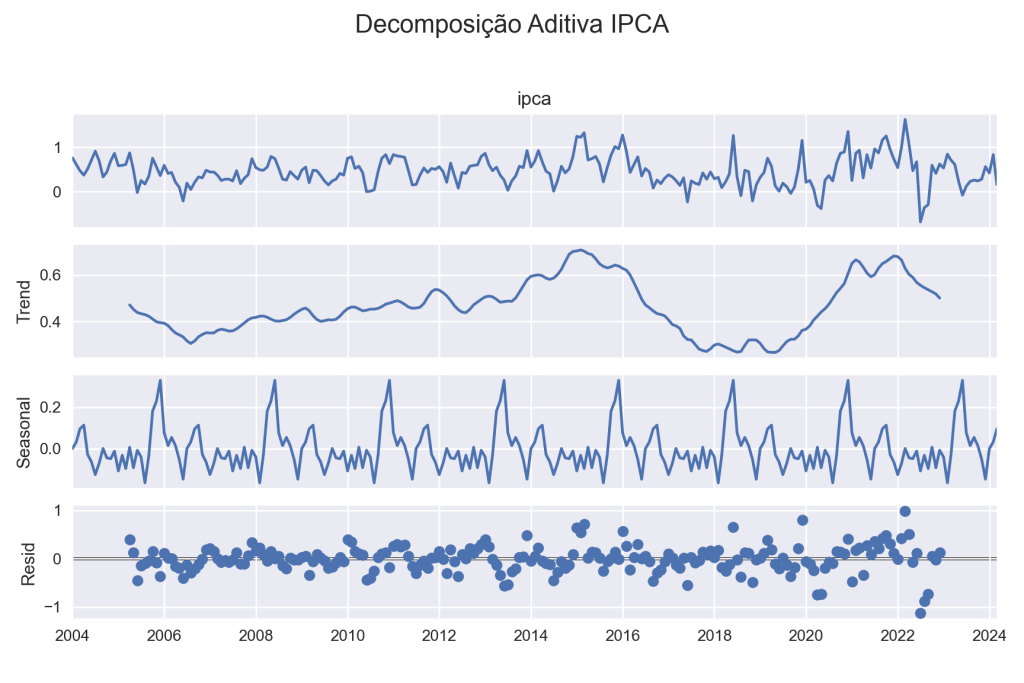
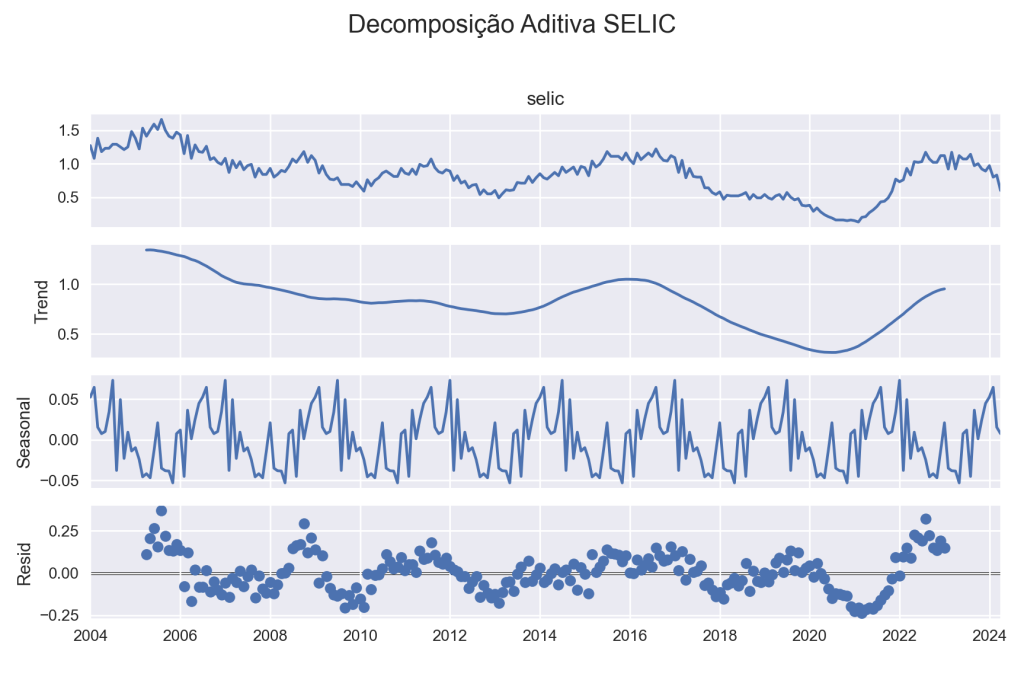
Decomposição
A decomposição de uma série temporal permite avaliar a tendência, a sazonalidade e os valores restantes se retirado estes dois componentes.
Autocorrelação
Assim como a correlação mede a relação linear entre duas variáveis, a autocorrelação mede a relação linear entre os valores defasados de uma série temporal.
Existem vários coeficientes de autocorrelação, por exemplo: mede a relação entre
e
,
mede a relação entre
e
, e assim por diante. Generalizando, analisamos a autocorrelação pela chamada função de autocorrelação (ACF), o que constitui uma etapa fundamental para corretamente especificar modelos.
IPCA
Os blocos azuis indicam se as correlações são significativamente diferentes de zero. Para uma série de ruído branco, é esperado que cada autocorrelação seja próxima de zero, entretando, elas não serão exatamente iguais a zero, pois há alguma variação aleatória.
Note que quando temos tendência, ou seja, não estacionariedade em uma série, as autocorrelações para pequenas defasagens tendem a ser grandes e positivas porque as observações próximas no tempo também estão próximas em valor.
Referências
Enders, W. 2009. Applied Econometric Times Series. Wiley Series in Probability and Statistics. Wiley.
Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.
Morettin, Pedro A., and Clélia Toloi. 2006. Análise de séries temporais. Editora Blucher.
Pfaff, B. 2008. Analysis of Integrated and Cointegrated Time Series with R. Second. New York: Springer.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.