Medindo o repasse da taxa Selic para o mercado de crédito bancário

No post de hoje, iremos replicar o estudo presente no boxe do RI 2022/09 do Banco Central, que mensura a magnitude da taxa Selic para diversas modalidades de crédito utilizando o R.

O estudo tem como principal objetivo estimar a magnitude dos repasses das alterações da Selic para as taxas de juros do Sistema Financeiro
Nacional (SFN), especificadamente as diferentes modalidades de crédito ofertados de acordo com os segmentos, sendo as presentes no estudo:

em PF livres:

aquisição de outros bens,
aquisição de veículos,
cheque especial
e crédito pessoal;

em PJ Livres,

aquisição de outros bens,
conta garantida
e cheque especial
desconto de duplicatas e recebíveis
capital de giro
compror e vendor
ACC
repasse externo

em PF direcionados,

imobiliário
rural

em PJ direcionados:

Banco Nacional de Desenvolvimento Econômico e Social (BNDES);
rural

A replica do estudo segue algumas alterações em relação ao Boxe. Em primeiro lugar, o estudo original utiliza uma série de Créditos Livres estendida por meio de outras fontes e interligadas por uma harmonização. Em segundo lugar, é utilizado em sua equação a adição de uma dummy em nível da série, o que não foi realizado nesta réplica.

Ao fim, temos aqui uma equação da seguinte forma, que é constituída por uma regressão linear estimada por MQO:

$\Delta Juros_{m,t} = \alpha_{m} + \sum_{i=0}^{11}\beta_{m,i} \Delta Selic_{t-1} + \sum_{i=0}^{3}\delta_{m,t-1}+ \Delta Inad_{m,t-1} + \varepsilon$

Seguindo o estudo, temos que o termo $\Delta Juros_{m,t}$ mede a variação no período da taxa de juros da modalidade; $\Delta Selic_{t-1}$ representa a variação da taxa Selic; $\Delta Inad_{m,t-1}$ representa a variação da taxa de inadimplência da modalidade.

Em relação aos coeficientes, $\alpha_{m}$ é uma constante, $\beta_{m,i}$ mede a magnitude do repasse de cada defasagem da Selic, $\delta_{m,t-1}$ mede o efeito da inadimplência e das suas defasagens.

Por fim, vamos construir o código em R. O objetivo será construir um método de coleta das variáveis utilizadas no estudo, realizar o respectivo tratamento, e "rodar" o modelo das 16 modalidades.

Começamos carregando os pacote utilizados.


library(tidyverse)
library(GetBCBData)
library(tsibble)
library(timetk)
library(dynlm)
library(broom)

Vamos coletar os dados através do Banco Central, coletadas por meio do pacote {GetBCBData}, com os respectivos códigos de cada série.


## Coleta de dados

totais <- c(
### Taxa de juros do crédito livre
"livre_fisico" = 20740,
"livre_juridico" = 20718,
### Taxa de juros do crédito direcionado
"direcionado_fisico" = 20768,
"direcionado_juridico" = 20757
)

modalidades <- c(
### Taxa de juros do crédito PF - livre
"pf_livre_outros" = 20750,
"pf_livre_veiculos" = 20749,
"pf_livre_cq_especial" = 20741,
"pf_livre_cq_pessoal" = 20748,
### Taxa de juros do crédito PF - Direcionado
"pf_direcionado_imob" = 20774,
"pf_direcionado_rural" = 20771,
### Taxa de juros do crédito PJ - Livres
"pj_livre_outros" = 20729,
"pj_livre_cont_g" = 20726,
"pj_livre_dd" = 20719,
"pj_livre_cap_giro" = 20725,
"pj_livre_compror" = 20735,
"pj_livre_acc" = 20736,
"pj_livre_repasse" = 20739,
### Taxa de juros do crédito PJ - Direcionados
"pj_direcionado_bndes" = 20765,
"pj_direcionado_rural" = 20760
)

inadimplencia <- c(
### Taxa de juros do crédito PF - livre
"pf_livre_outros_inad" = 21122,
"pf_livre_veiculos_inad" = 21121,
"pf_livre_cq_especial_inad" = 21113,
"pf_livre_cq_pessoal_inad" = 21120,
### Taxa de juros do crédito PF - Direcionado
"pf_direcionado_imob_inad" = 21151,
"pf_direcionado_rural_inad" = 21148,
### Taxa de juros do crédito PJ - Livres
"pj_livre_outros_inad" = 21097,
"pj_livre_cont_g_inad" = 21094,
"pj_livre_dd_inad" = 21087,
"pj_livre_cap_giro_inad" = 21093,
"pj_livre_compror_inad" = 21103,
"pj_livre_acc_inad" = 21107,
"pj_livre_repasse_inad" = 21110,
### Taxa de juros do crédito PJ - Direcionados
"pj_direcionado_bndes_inad" = 21143,
"pj_direcionado_rural_inad" = 21136
)

##
data_inicio = "2011-03-01"

creditos_totais <- GetBCBData::gbcbd_get_series(
id = totais,
use.memoise = FALSE,
first.date = data_inicio
)

modalidades_creditos <- GetBCBData::gbcbd_get_series(
id = modalidades,
use.memoise = FALSE,
first.date = data_inicio
)

inadimplencia_series <- GetBCBData::gbcbd_get_series(
id = inadimplencia,
use.memoise = FALSE,
first.date = data_inicio
)

selic_raw <- GetBCBData::gbcbd_get_series(
id = c("selic" = 4189),
use.memoise = FALSE,
first.date = data_inicio
)

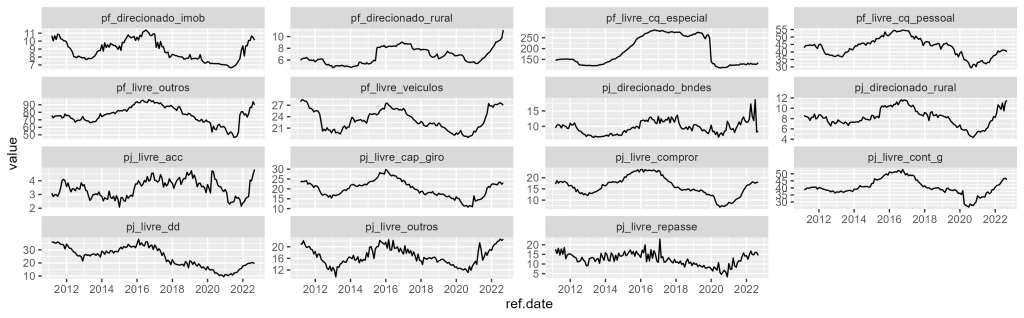
Analisamos a série de cada modalidade abaixo, por meio da construção do gráfico de série temporal com o ggplot2.


## Visualização

ggplot(modalidades_creditos, aes(x = ref.date, y = value))+
geom_line()+
facet_wrap(~series.name, scales = "free_y")

Na parte de tratamento, devemos transformar as séries (isto é, calcular a variação) e defasar os valores da Selic e Inadimplência. Utilizamos o pacote {tsibble} e o {timetk} para auxiliar no processo.


## Tratamento

### Modalidade de crédito

modalidades_creditos_tt <- modalidades_creditos |>
select("date" = ref.date,
value,
"modalidade" = series.name) |>
pivot_wider(names_from = modalidade,
values_from = value) |>
mutate(date = yearmonth(date)) |>
as_tsibble(index = date)

modalidades_creditos_diff <- modalidades_creditos_tt %>%
dplyr::transmute(
dplyr::across(
.cols = !"date",
.fns = ~tsibble::difference(
x = .x,
differences = 1
),
.names = "{col}_diff"
)
)

### Inadimplência

inadimplencia_tt <- inadimplencia_series |>
select("date" = ref.date,
value,
"inadimplencia" = series.name) |>
pivot_wider(names_from = inadimplencia,
values_from = value) |>
mutate(date = yearmonth(date)) |>
as_tsibble(index = date)

# Calcula o delta

inadimplencia_diff <- inadimplencia_tt %>%
dplyr::transmute(
dplyr::across(
.cols = !"date",
.fns = ~tsibble::difference(
x = .x,
differences = 1
),
.names = "{col}_diff"
)
) |>
timetk::tk_augment_lags(.value = contains(c("pf", "pj")),
.lags = 1:3)

### Selic

selic_tt <- selic_raw |>
select("date" = ref.date,
"selic" = value)

# Calcula o delta

selic_diff <- selic_tt |>
transmute(date = date,
selic_diff = selic - lag(selic)) |>
timetk::tk_augment_lags(.value = "selic_diff",
.lags = 1:12)|>
mutate(date = yearmonth(date)) |>
as_tsibble(index = date)

### Junta os dados

all_data <- modalidades_creditos_diff |>
full_join(inadimplencia_diff, by = 'date') |>
full_join(selic_diff, by = 'date')

Estamos lidando com diversas variáveis e precisamos agora rodar diversos modelos de regressão linear, para tanto, criamos um código que permita transformar cada equação de uma modalidade em um data frame dentro de uma lista e aplicamos a função dynlm() (para rodar a regressão) em conjunto com a função map() do pacote {purrr}.


### Cria um loop para criar uma lista contendo as variáveis de cada modelo

dep_variables <- names(modalidades)

my_list <- list()

for(i in dep_variables){
df <- all_data |> select(starts_with(c(i, "selic")))
my_list[[i]] <- df
}

# Renomeia as variáveis do modelo para nomes padrão

all_variables <-c("delta_juros", "delta_inad", "delta_inad_lag1", "delta_inad_lag2", "delta_inad_lag3", colnames(selic_diff)[-1], "date")

lm_data <- lapply(my_list, `names<-`, all_variables)

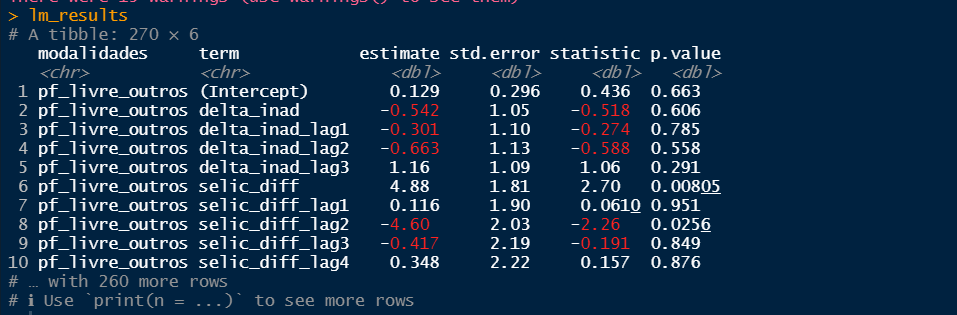
Agora, é possível rodar a regressão e extrair os parâmetros do modelo de cada modalidade com o pacote {broom}.


# Aplica a regressão linear em cada data frame da lista

lm_results <- map(lm_data, ~dynlm::dynlm(delta_juros ~ . - date, data = .)) |>
map(broom::tidy) |>
bind_rows(.id = "modalidades")

lm_results

Quer saber mais?

Veja a nossa trilha de Macroeconomia Aplicada.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Como coletar dados do Eurostat usando a API com o Python?

Estimando a volatilidade da taxa de câmbio

Como analisar o Núcleo de Inflação no Brasil usando Python?

Propensity Score com Múltiplas Variáveis no R

Análise regional da inflação com dados do IBGE usando Python

Como coletar dados do Banco Central do Chile usando a API com o Python?

Outros artigos relacionados

Como coletar dados do Eurostat usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal Eurostat através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.

Estimando a volatilidade da taxa de câmbio

O que é Volatilidade? Como podemos calcular essa métrica? Este artigo apresenta uma breve introdução à volatilidade, descreve como podemos calcular a volatilidade utilizando Modelos de Volatilidade Condicional e demonstra a aplicação prática dessa abordagem para estimar a volatilidade da taxa de câmbio BRL/USD por meio da linguagem de programação Python.

Como analisar o Núcleo de Inflação no Brasil usando Python?

O Python se destaca como uma ferramenta robusta para análise de dados, permitindo a aplicação de uma ampla gama de técnicas em dados econômico-financeiros. Neste exercício, destacamos como a linguagem oferece uma facilidade muito grande na coleta de dados dos núcleos do IPCA diretamente do site do Banco Central, na manipulação eficiente desses dados e na construção de gráficos que facilitam a compreensão dos indicadores.