A Lei de Okun é uma relação empírica que busca quantificar a relação entre a taxa de desemprego e a taxa de crescimento econômico. Ela foi proposta pelo economista Arthur Okun na década de 1960 e está presente em diversos livros textos de graduação. Buscamos através deste artigo investigar duas formas da Lei de Okun, descrevendo-a utilizando dados do Brasil. Usamos o Python para realizar todo o processo de análise de dados.
Relações empíricas relacionadas ao desemprego têm fascinado os economistas por muito tempo. Por exemplo, a curva de Phillips começou como uma simples observação de trade-off entre desemprego e inflação. No entanto, à medida que a teoria se alinhou com as evidências, a curva de Phillips emergiu como a relação mais importante na maneira como os economistas enxergam o lado da oferta da economia e está incorporada em todos os principais modelos macroeconômicos que orientam as políticas atualmente.
Outra relação de interesse para os economistas é aquela entre produção e desemprego. Em 1962, Arthur Okun observou duas relações empíricas:
- as mudanças trimestrais na taxa de desemprego estavam relacionadas ao crescimento trimestral do produto interno bruto (PIB) real
- desvios na taxa de desemprego estavam relacionados aos desvios do PIB em relação ao seu potencial (isto é, o Hiato do Produto)
Essas relações ficaram conhecidas como as versões differences e gaps da Lei de Okun, respectivamente.
A Lei de Okun é considerada uma relação estatística em vez de uma característica estrutural da economia, uma vez que tornou-se instável a sua aplicação. Isso corrobora como qualquer tipo de relação estatística, que pode estar sujeita a rupturas estruturais ou mudanças de regime. Por exemplo, mudanças estruturais no mercado de trabalho que levam a alterações na taxa de desemprego não aceleradora de inflação (NAIRU) são consideradas capazes de modificar o nível de equilíbrio do desemprego e alterar o trade-off entre inflação e produção. Embora esses choques do lado da oferta estejam cada vez mais integrados à teoria econômica, as rupturas estruturais na relação entre produção e desemprego limitaram o uso da Lei de Okun como uma regra de previsão.
Embora esses problemas tenham diminuido a confiança no uso da Lei de Okun, ainda podemos utiliza-la como uma regra de bolso simples e prática. Portanto, vamos aplicar tanto o método differences quanto o gaps.
Para dados do desemprego utilizaremos a Taxa de Desocupação medida pela PNADc ampliada e dessazonalizada, criada pelo exercício “Ampliando a série da PNADc”da Análise Macro. A importância de uma série ampliada permite que tenhamos uma amostra de tamanho suficiente, visto que utilizaremos dados trimestrais e a série da PNADc tem início em 2012.
Para dados de crescimento, utilizaremos Taxa de Variação T/T-1 do PIB a preços de mercado ajustado sazonalmente. E para o Hiato do Produto, capturamos os dados produzidos pelo Banco Central do Brasil, obtido através do Relatório de Inflação.
Lei de Okun: differences
A versão differences da Lei de Okun busca relacionar a variação da Taxa de de desemprego T/T-1 contemporaneamente com a variação da Taxa de Crescimento do PIB T/T-1.
Onde:
- é a mudança na taxa de desemprego no período
contra
,
- é a mudança no PIB real no período
contra
,
- é o coeficiente de Okun, que representa a sensibilidade da taxa de desemprego às mudanças no PIB. É esperado que seja negativo, para representar a relação inversa
- é o termo constante, valor para quando há 0% de variação na taxa de crescimento.
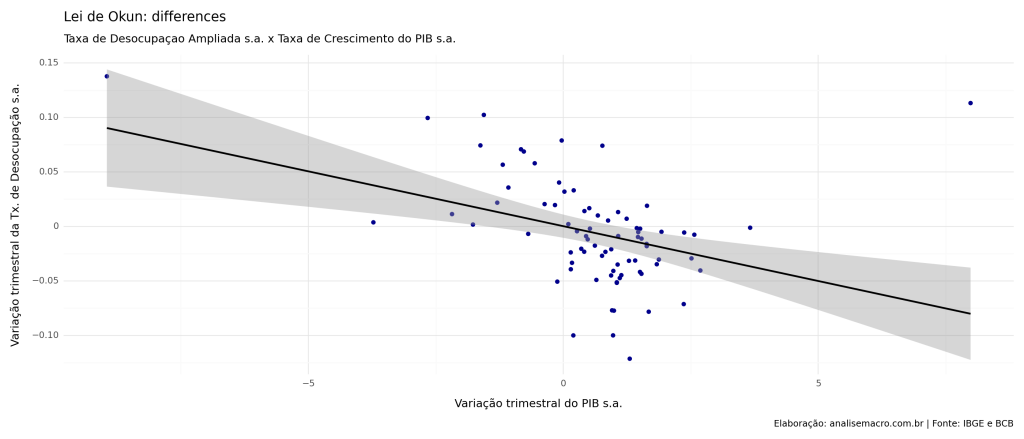
O gráfico de dispersão abaixo confirma que há de fato uma relação inversa para os dados selecionados.
Os resultados da regressão linear confirmam que a relação entre as duas variáveis é negativa e significativa. O coeficiente de regressão () é o coeficiente de Okun, e significa que uma variação de 1% na Taxa de Crescimento, ocasiona, em média, uma variação de -0.0101% na Taxa de Desemprego.
A razão fornece a taxa de crescimento do produto consistente com uma taxa de desemprego estável, ou seja, quão rápido a economia precisaria crescer tipicamente para manter a taxa de desemprego existente. Neste caso,
.
Código
OLS Estimation Summary
=================================================================================
Dep. Variable: pnad_ampliada_sa_diff R-squared: 0.1450
Estimator: OLS Adj. R-squared: 0.1339
No. Observations: 79 F-statistic: 13.402
Date: Fri, Dec 08 2023 P-value (F-stat) 0.0003
Time: 11:41:26 Distribution: chi2(1)
Cov. Estimator: unadjusted
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.0002 0.0053 0.0390 0.9689 -0.0102 0.0106
pib_marg -0.0101 0.0027 -3.6609 0.0003 -0.0155 -0.0047
==============================================================================Código
0.02050036209582354
Isso significa que seria necessário um crescimento de 0.0205% a cada trimestre para que a taxa de desemprego permaneça constante, aproximando-se de sua média de longo prazo.
Lei de Okun: output gap
Esta versão da lei relaciona as mudanças na taxa de desemprego ao hiato entre a produção real e a produção potencial ou tendencial. Portanto, se a produção cair abaixo do potencial, abrindo um hiato negativo, espera-se que o desemprego aumente. Vice-versa, quando a produção real está acima da tendência ou potencial e surge um hiato positivo, espera-se que o desemprego diminua. Semelhante à versão differences, isso enfatiza a importância do ciclo econômico na determinação das mudanças no desemprego.
No entanto, não há uma definição universal do que constitui a produção ‘tendencial’ ou ‘potencial’, mas geralmente se pensa como sendo o nível de produção uma vez que medidas cíclicas e idiossincráticas foram removidas. Nesse sentido, é um nível de equilíbrio de produção no qual a economia pode crescer sem experimentar pressões inflacionárias ou deflacionárias. Outra maneira de expressar isso é definir a produção tendencial como o nível de produção consistente com o desemprego estando em sua NAIRU. Quando a produção ultrapassa a tendência, o desemprego cai abaixo de sua NAIRU e vice-versa.
Onde:
- é a taxa de desemprego no período
,
- é a taxa de desemprego no estado estacionário (ou NAIRU) no período
,
- é o PIB real no período
,
- é o PIB potencial no período
,
- é um coeficiente que representa a sensibilidade da taxa de desemprego aos desvios do PIB em relação ao seu potencial.
O problema nesta versão se concentra na impossibilidade de observar diretamente o produto potencial e a NAIRU, sendo necessário estimativas dessas medidas, o que pode tornar os valores da relação diferentes para cada diferentes método empregado para realizar a estimação.
Para o caso do Hiato, utilizaremos os dados disponibilizados pelo BCB, que estima o produto potencial através de uma função de produção. Para a NAIRU, utilizaremos o filtro hp, que permite remover oscilações, suavizando inovações de curto prazo (cíclicas e idiossincráticas).
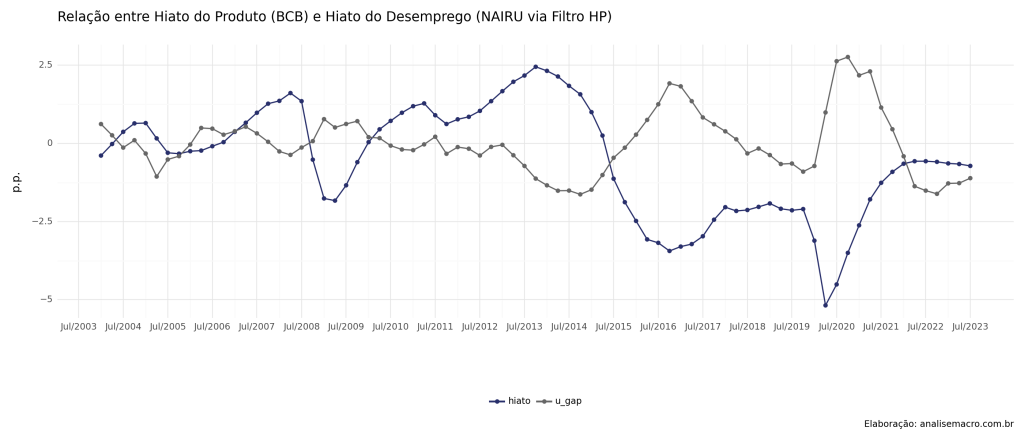
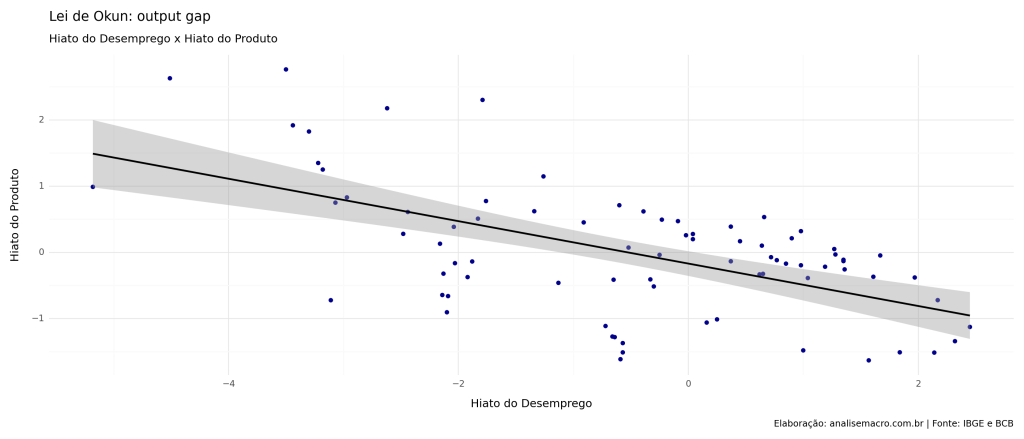
Através do gráfico de dispersão abaixo, podemos confirmar que há a relação inversa contemporânea, proposta pela Lei de Okun. Esta evidência é corroborada ao analisarmos o hiato do desemprego e do produto ao longo do tempo.
A relação estimada através de uma regressão linear, aliás, é muito mais forte do aquela encontrada pela versão de diferenças, exibindo um coeficiente de valor mais alto, e R² maior.
Código
OLS Estimation Summary
==============================================================================
Dep. Variable: u_gap R-squared: 0.3068
Estimator: OLS Adj. R-squared: 0.2979
No. Observations: 79 F-statistic: 34.961
Date: Fri, Dec 08 2023 P-value (F-stat) 0.0000
Time: 11:41:28 Distribution: chi2(1)
Cov. Estimator: unadjusted
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
hiato -0.2934 0.0496 -5.9128 0.0000 -0.3907 -0.1961
==============================================================================Considerações
Por mais que a Lei de Okun tenha seus defeitos, ainda pode servir de regra de bolso para o caso brasileiro, permitindo tornar as análises da relação do desemprego e do produto mais críveis.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.