Introdução
Todo analista de dados conhece a sensação: um gráfico que simplesmente não parece certo. Desde o início de 2022, um desses gráficos tem dominado as discussões macroeconômicas. Ele mostra duas linhas que historicamente dançaram em um ritmo semelhante – o índice S&P 500 e o número de vagas de emprego em aberto (JOLTS) – de repente se separando em uma divergência dramática, formando o que muitos apelidaram de “boca de jacaré”.
Esta anomalia visual levanta questões fundamentais. Estaríamos testemunhando uma mudança estrutural, talvez acelerada pela ascensão da IA generativa, que quebrou a relação tradicional entre os mercados financeiros e a economia real? Ou seria esta divergência apenas um eco amplificado de um ciclo macroeconômico clássico, impulsionado pelo aperto monetário mais agressivo em quarenta anos?
Neste post, vamos mergulhar fundo nessa questão. Usaremos os próprios gráficos como nosso guia, começando pela evidência visual que gerou o debate, e então empregaremos um modelo de Vetor Autorregressivo (VAR) para submeter nossas hipóteses ao rigor estatístico.
Trajetória JOLTS x S&P 500
Para comparar duas séries de magnitudes tão distintas, a normalização é essencial. Ao escalar tanto o S&P 500 quanto as vagas em aberto para um intervalo de 0 a 1, podemos focar em suas tendências relativas.
O gráfico resultante é impressionante. Até 2022, as duas séries exibem um comovimento notável. Ambas caem durante a crise de 2008, se recuperam juntas e disparam após o choque inicial da pandemia de COVID-19. A partir do início de 2022, no entanto, a relação se desfaz. O S&P 500 (em amarelo) inicia uma queda acentuada, enquanto as vagas em aberto (em azul) permanecem em níveis historicamente elevados, apenas começando a moderar muito mais tarde.
É neste contexto que a narrativa da IA ganha força, com o lançamento do ChatGPT em novembro de 2022 (marcado pela linha tracejada) ocorrendo em meio a essa divergência. A hipótese é que as empresas, antecipando ganhos de produtividade com a IA, mantiveram o otimismo para contratações mesmo com os mercados financeiros sinalizando problemas. Mas seria essa a história completa?
Um economista sabe que nenhuma variável opera no vácuo. O gráfico seguinte revela o “ator principal” que estava fora do palco no primeiro gráfico: a política monetária do Federal Reserve.
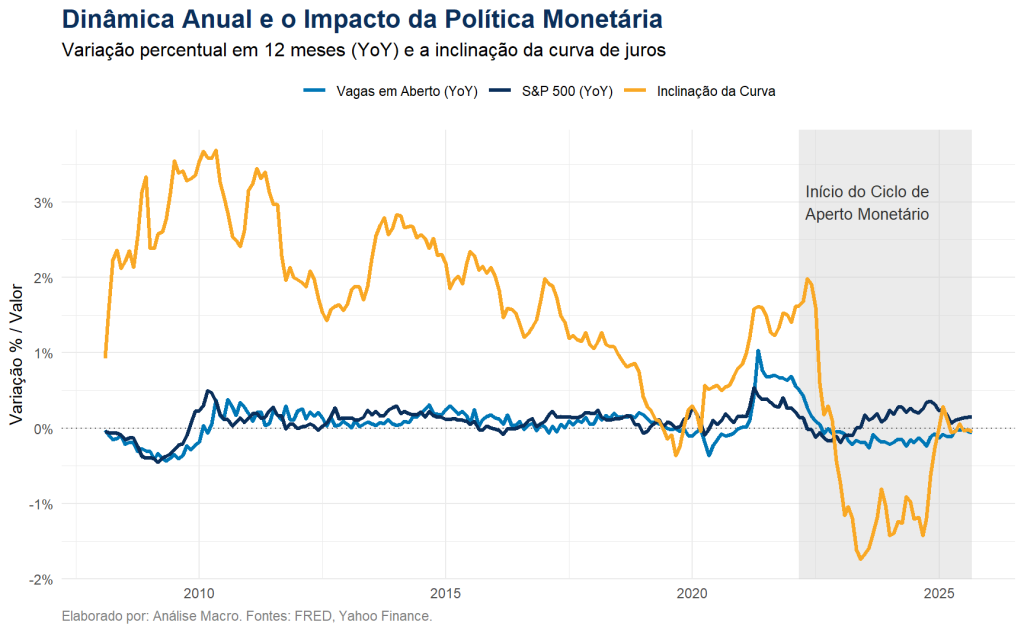
Este gráfico mostra duas coisas cruciais. Primeiro, a subida quase vertical da taxa de juros básica (Fed Funds Rate), destacada pela área sombreada a partir de março de 2022. Segundo, a consequente inversão da curva de juros (Inclinação da Curva), que mergulha em território negativo – um dos mais confiáveis preditores de recessão.
A mensagem visual é clara: o S&P 500, um ativo forward-looking extremamente sensível às taxas de juros e às expectativas de crescimento, reagiu imediatamente a este novo regime. O mercado de trabalho, no entanto, opera com inércia e fricções. A relutância das empresas em demitir (“labor hoarding”) após a experiência traumática da pandemia manteve a demanda por trabalho artificialmente alta. O gráfico sugere que a divergência não foi causada por um novo fator (como a IA), mas sim pela velocidade de reação drasticamente diferente dos mercados financeiros e do mercado de trabalho a um choque macroeconômico massivo e comum.
Vemos esse efeito mais claramente quando comparamos o S&P 500 e JOLTS em suas taxas de variação interanuais.
Análise Econométrica: causalidade sentido granger
A narrativa visual é convincente, mas para um econometrista, ela é apenas o ponto de partida. Para testar formalmente essas relações, construímos um modelo VAR(2) com as séries em variação anual (YoY), garantindo a estacionariedade e permitindo uma interpretação econômica direta.
Primeiro, é necessário confirmar a estacionariedade das séries temporais. Para isto, fazemos o uso do teste de estacionariedade ADF. Com valor crítico de 0.10, confirmamos que as 3 séries são estacionárias.
[1] "S&P 500 YoY p-valor: 0.0175"[1] "Jobs YoY p-valor: 0.0961"[1] "Yield Slope p-valor: 0.0652AIC(n) HQ(n) SC(n) FPE(n)
3 2 1 3 Código
# O número ótimo de lags 'p' é geralmente o que é sugerido pela maioria dos critérios (AIC, HQ, SC)[1] "Número de lags escolhido (p): 2"VAR Estimation Results:
=========================
Endogenous variables: sp500_yoy, jobs_yoy, yield_slope
Deterministic variables: const
Sample size: 210
Log Likelihood: 518.598
Roots of the characteristic polynomial:
0.974 0.8968 0.8968 0.3188 0.1919 0.002646
Call:
vars::VAR(y = dados_para_analise, p = p, type = "const")
Estimation results for equation sp500_yoy:
==========================================
sp500_yoy = sp500_yoy.l1 + jobs_yoy.l1 + yield_slope.l1 + sp500_yoy.l2 + jobs_yoy.l2 + yield_slope.l2 + const
Estimate Std. Error t value Pr(>|t|)
sp500_yoy.l1 0.977991 0.070753 13.823 <2e-16 ***
jobs_yoy.l1 -0.077218 0.053773 -1.436 0.153
yield_slope.l1 0.023109 0.020726 1.115 0.266
sp500_yoy.l2 -0.048404 0.074029 -0.654 0.514
jobs_yoy.l2 0.046817 0.050671 0.924 0.357
yield_slope.l2 -0.025257 0.021070 -1.199 0.232
const 0.012343 0.007989 1.545 0.124
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.06774 on 203 degrees of freedom
Multiple R-Squared: 0.8387, Adjusted R-squared: 0.8339
F-statistic: 175.9 on 6 and 203 DF, p-value: < 2.2e-16
Estimation results for equation jobs_yoy:
=========================================
jobs_yoy = sp500_yoy.l1 + jobs_yoy.l1 + yield_slope.l1 + sp500_yoy.l2 + jobs_yoy.l2 + yield_slope.l2 + const
Estimate Std. Error t value Pr(>|t|)
sp500_yoy.l1 0.330167 0.091698 3.601 0.000399 ***
jobs_yoy.l1 0.632717 0.069691 9.079 < 2e-16 ***
yield_slope.l1 0.002261 0.026861 0.084 0.933000
sp500_yoy.l2 -0.094288 0.095943 -0.983 0.326901
jobs_yoy.l2 0.195457 0.065670 2.976 0.003272 **
yield_slope.l2 0.011489 0.027307 0.421 0.674392
const -0.032931 0.010354 -3.181 0.001700 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.0878 on 203 degrees of freedom
Multiple R-Squared: 0.8584, Adjusted R-squared: 0.8542
F-statistic: 205.1 on 6 and 203 DF, p-value: < 2.2e-16
Estimation results for equation yield_slope:
============================================
yield_slope = sp500_yoy.l1 + jobs_yoy.l1 + yield_slope.l1 + sp500_yoy.l2 + jobs_yoy.l2 + yield_slope.l2 + const
Estimate Std. Error t value Pr(>|t|)
sp500_yoy.l1 0.436717 0.224675 1.944 0.0533 .
jobs_yoy.l1 -0.127661 0.170754 -0.748 0.4555
yield_slope.l1 1.274901 0.065815 19.371 < 2e-16 ***
sp500_yoy.l2 -0.304441 0.235075 -1.295 0.1968
jobs_yoy.l2 0.033214 0.160903 0.206 0.8367
yield_slope.l2 -0.285801 0.066906 -4.272 2.98e-05 ***
const 0.000451 0.025368 0.018 0.9858
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2151 on 203 degrees of freedom
Multiple R-Squared: 0.9747, Adjusted R-squared: 0.974
F-statistic: 1305 on 6 and 203 DF, p-value: < 2.2e-16
Covariance matrix of residuals:
sp500_yoy jobs_yoy yield_slope
sp500_yoy 0.0045893 0.0009498 -0.0002658
jobs_yoy 0.0009498 0.0077085 -0.0009284
yield_slope -0.0002658 -0.0009284 0.0462763
Correlation matrix of residuals:
sp500_yoy jobs_yoy yield_slope
sp500_yoy 1.00000 0.15969 -0.01824
jobs_yoy 0.15969 1.00000 -0.04916
yield_slope -0.01824 -0.04916 1.00000Teste de especificação do VAR
Abaixo verificamos a autocorrelação e normalidade do modelo VAR:
Autocorrelação
Código
Portmanteau Test (asymptotic)
data: Residuals of VAR object modelo_var
Chi-squared = 255.15, df = 126, p-value = 8.662e-11Normalidade
Código
$JB
JB-Test (multivariate)
data: Residuals of VAR object modelo_var
Chi-squared = 1435.4, df = 6, p-value < 2.2e-16
$Skewness
Skewness only (multivariate)
data: Residuals of VAR object modelo_var
Chi-squared = 140.01, df = 3, p-value < 2.2e-16
$Kurtosis
Kurtosis only (multivariate)
data: Residuals of VAR object modelo_var
Chi-squared = 1295.4, df = 3, p-value < 2.2e-16Teste Causalidade sentido Granger
Resultado 1:
- Hipótese: A variação do S&P 500 Granger-causa a variação das vagas em aberto.
- Resultado: p-valor = 3.68e-05. Hipótese nula rejeitada.
Interpretação: Este é o resultado mais forte da nossa análise. Ele confirma estatisticamente o que os gráficos sugerem: a performance do mercado de ações é um poderoso indicador antecedente para o mercado de trabalho. As expectativas dos investidores, que derrubaram o S&P 500 em 2022, continham informação valiosa que precedeu a eventual desaceleração na criação de vagas.
Resultado 2:
- Hipótese: A variação das vagas em aberto Granger-causa a variação do S&P 500.
- Resultado: p-valor = 0.4165. Hipótese nula não rejeitada.
Interpretação: A resiliência do mercado de trabalho, embora tenha sido o foco de muitas análises, não demonstrou ter poder preditivo sobre a direção do mercado de ações. O S&P 500 estava mais focado no aperto monetário e nas expectativas de recessão do que nos dados retroativos de um mercado de trabalho ainda aquecido por fatores pós-pandêmicos.
Resultado 3:
- Hipótese: A inclinação da curva de juros Granger-causa o sistema.
- Resultado: p-valor = 0.0789. Hipótese nula rejeitada (a 10%).
Interpretação: Este resultado valida a nossa narrativa visual. A inclinação da curva, nosso proxy para as expectativas do ciclo econômico e da política monetária, é um motor causal para ambas as variáveis. Isso reforça a conclusão de que o choque de política monetária foi o evento iniciador que desencadeou as dinâmicas subsequentes.
Código
# Teste 1: S&P 500 YoY causa Jobs YoY?
# H0: sp500_yoy NÃO Granger-causa jobs_yoy
causality_sp_to_jobs <- vars::causality(modelo_var, cause = "sp500_yoy", vcov. = sandwich::vcovHC(modelo_var))
print("--- H0: S&P 500 YoY NÃO Granger-causa Jobs YoY ---")[1] "--- H0: S&P 500 YoY NÃO Granger-causa Jobs YoY ---"Código
print(causality_sp_to_jobs)$Granger
Granger causality H0: sp500_yoy do not Granger-cause jobs_yoy
yield_slope
data: VAR object modelo_var
F-Test = 6.545, df1 = 4, df2 = 609, p-value = 3.68e-05
$Instant
H0: No instantaneous causality between: sp500_yoy and jobs_yoy
yield_slope
data: VAR object modelo_var
Chi-squared = 5.2434, df = 2, p-value = 0.07268Código
# Teste 2: Jobs YoY causa S&P 500 YoY?
# H0: jobs_yoy NÃO Granger-causa sp500_yoy
causality_jobs_to_sp <- vars::causality(modelo_var, cause = "jobs_yoy", vcov. = sandwich::vcovHC(modelo_var))
print("--- H0: Jobs YoY NÃO Granger-causa S&P 500 YoY ---")[1] "--- H0: Jobs YoY NÃO Granger-causa S&P 500 YoY ---"Código
print(causality_jobs_to_sp)$Granger
Granger causality H0: jobs_yoy do not Granger-cause sp500_yoy
yield_slope
data: VAR object modelo_var
F-Test = 0.98244, df1 = 4, df2 = 609, p-value = 0.4165
$Instant
H0: No instantaneous causality between: jobs_yoy and sp500_yoy
yield_slope
data: VAR object modelo_var
Chi-squared = 5.6481, df = 2, p-value = 0.05936Código
# Testes adicionais para entender a dinâmica completa
# Yield Slope causa S&P 500 YoY?
causality_yield_to_sp <- vars::causality(modelo_var, cause = "yield_slope", vcov. = sandwich::vcovHC(modelo_var))
print("--- H0: Yield Slope NÃO Granger-causa S&P 500 YoY ---")[1] "--- H0: Yield Slope NÃO Granger-causa S&P 500 YoY ---"Código
print(causality_yield_to_sp)$Granger
Granger causality H0: yield_slope do not Granger-cause sp500_yoy
jobs_yoy
data: VAR object modelo_var
F-Test = 2.1036, df1 = 4, df2 = 609, p-value = 0.07891
$Instant
H0: No instantaneous causality between: yield_slope and sp500_yoy
jobs_yoy
data: VAR object modelo_var
Chi-squared = 0.52936, df = 2, p-value = 0.7675Código
# Yield Slope causa Jobs YoY?
causality_yield_to_jobs <- vars::causality(modelo_var, cause = "yield_slope", vcov. = sandwich::vcovHC(modelo_var))
print("--- H0: Yield Slope NÃO Granger-causa Jobs YoY ---")[1] "--- H0: Yield Slope NÃO Granger-causa Jobs YoY ---"Código
print(causality_yield_to_jobs)$Granger
Granger causality H0: yield_slope do not Granger-cause sp500_yoy
jobs_yoy
data: VAR object modelo_var
F-Test = 2.1036, df1 = 4, df2 = 609, p-value = 0.07891
$Instant
H0: No instantaneous causality between: yield_slope and sp500_yoy
jobs_yoy
data: VAR object modelo_var
Chi-squared = 0.52936, df = 2, p-value = 0.7675Conclusão
A “boca de jacaré” que intrigou tantos analistas não parece ser o sinal de uma nova era impulsionada pela IA, mas sim a manifestação visual de um ciclo macroeconômico clássico, exacerbado pelas condições únicas do pós-pandemia.
Os gráficos nos contaram uma história de reação em duas velocidades: a resposta instantânea e brutal dos mercados financeiros a um aperto monetário agressivo, e a reação lenta e retardada de um mercado de trabalho com fricções estruturais.
Embora o impacto da IA no mercado de trabalho seja uma questão crucial para o futuro, a grande divergência de 2022-2023 tem uma explicação mais imediata e fundamentada nos princípios da macroeconomia. Os gráficos nos mostraram o que aconteceu, e a econometria nos explicou o porquê.