Desde a metade do primeiro semestre de 2023 a temperatura das águas do Oceano Pacífico equatorial se elevaram, atingindo um ponto de anomalia em agosto (NOOA). Este fenômeno é conhecido como “El Niño” e tem impactos generalizados em diversas áreas do globo, podendo afetar a precipitação e temperatura, que são fatores chave para o plantio e colheita de diversas culturas.
Para mensurar os efeitos do El Niño sobre os preços da alimentação dos brasileiros, neste artigo estimamos um modelo de vetores autoregressivos de ordem p ou, simplesmente, VAR(p), baseado em BCB (2019):
Para mensurar os efeitos do El Niño sobre os preços da alimentação dos brasileiros, neste artigo estimamos um modelo de vetores autoregressivos de ordem p ou, simplesmente, VAR(p), baseado em BCB (2019):
![\[y_t = \sum_{i=1}^p A_p y_{t-p} + z_t + \varepsilon_t\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-1fb1f06caaeb567753350b08b6e31fdb_l3.png "Rendered by QuickLaTeX.com")
onde:
- 
- 
é a taxa de inflação medida pelo IPCA, subgrupo alimentação no domicílio
- 
é o hiato do produto medido pela função de produção
- 
é a inflação externa, medida pelo Índice de Commodities - Brasil agropecuário
- 
é o Oceanic Niño Index (ONI), transformado como 
- 
inclui uma constante e dummies sazonais
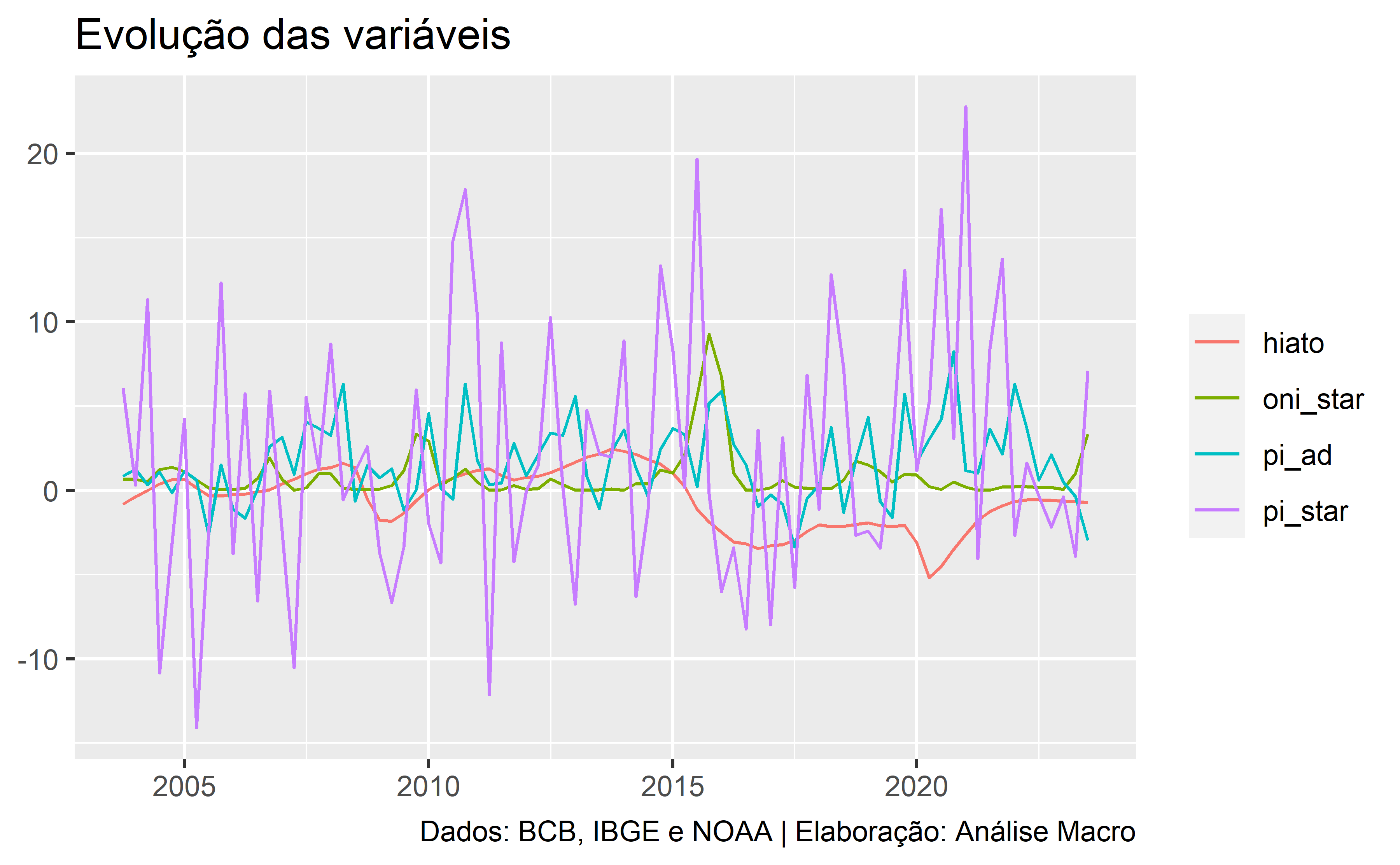
Utilizamos uma amostra de dados do quarto trimestre de 2003 ao terceiro trimestre de 2023. Outras informações e detalhes podem ser encontradas em BCB (2019). Os dados em frequência trimestral são expostos no gráfico abaixo:
Abaixo exibimos os resultados estatísticos do modelo VAR:
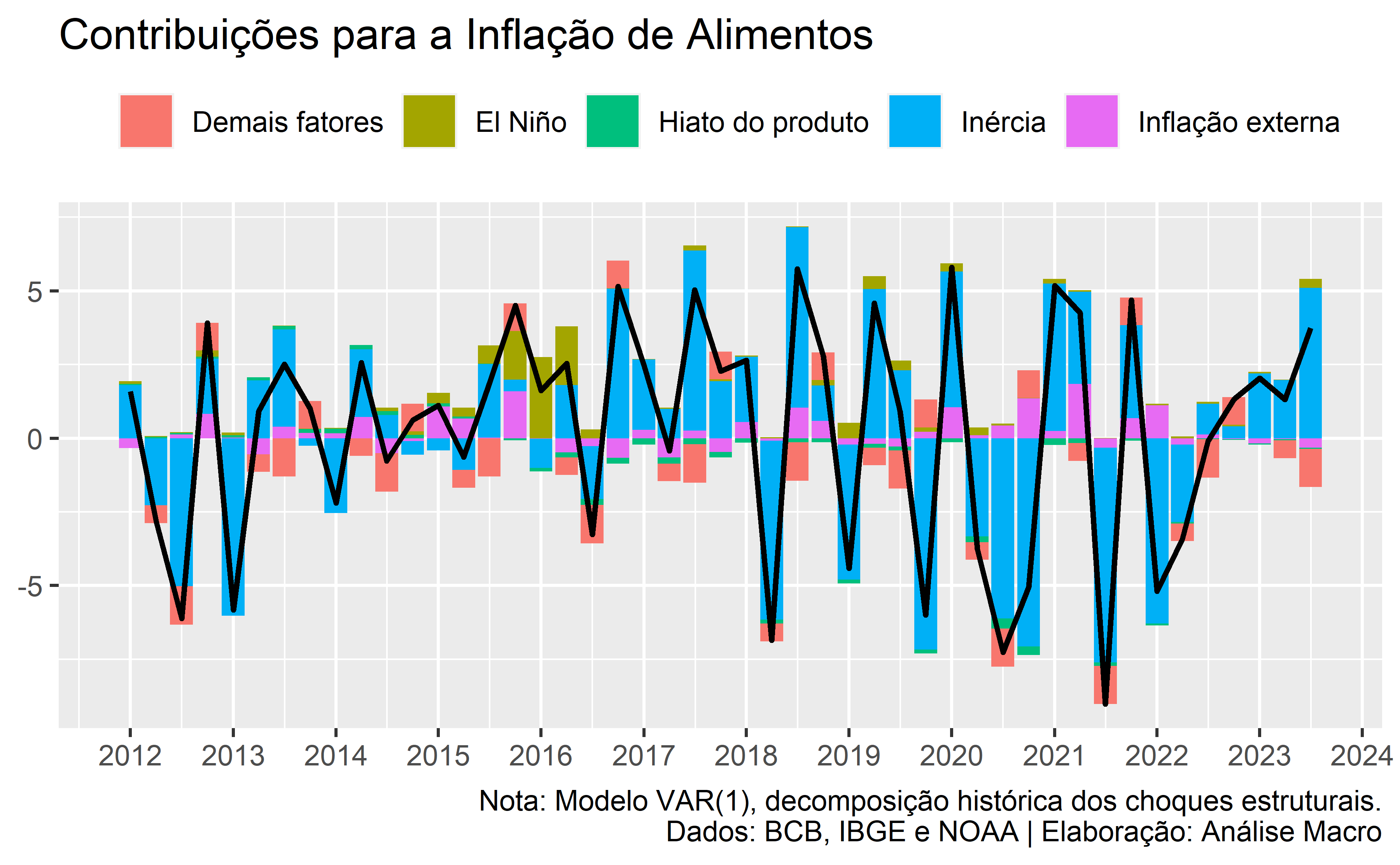
Series: oni_star, pi_star, hiato, pi_ad Model: VAR(3) w/ mean Coefficients for oni_star: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 1.3077 0.0189 -0.1454 -0.0633 s.e. 0.1280 0.0141 0.2437 0.0522 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) -0.8657 0.0056 -0.0028 0.0216 s.e. 0.1845 0.0151 0.4201 0.0521 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant 0.2629 0.0008 0.1916 -0.0211 -0.1488 s.e. 0.1343 0.0148 0.2420 0.0497 0.2575 season().year2 season().year3 season().year4 0.3957 0.9270 0.6599 s.e. 0.3224 0.3201 0.3136 Coefficients for pi_star: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 0.3929 -0.1429 -1.8525 0.7254 s.e. 1.1553 0.1269 2.1994 0.4710 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) -2.2887 0.1106 4.1782 -0.2966 s.e. 1.6649 0.1362 3.7911 0.4699 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant 1.1749 0.1617 -2.8212 -0.1620 0.5076 s.e. 1.2122 0.1340 2.1837 0.4481 2.3239 season().year2 season().year3 season().year4 -2.7310 1.7834 4.7214 s.e. 2.9092 2.8882 2.8295 Coefficients for hiato: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) -0.1230 0.0065 1.7018 0.0027 s.e. 0.0627 0.0069 0.1193 0.0255 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) 0.1914 -0.0104 -1.0377 -0.0286 s.e. 0.0903 0.0074 0.2056 0.0255 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant -0.1709 -0.0038 0.2652 0.0531 -0.0397 s.e. 0.0658 0.0073 0.1184 0.0243 0.1261 season().year2 season().year3 season().year4 -0.0053 0.1549 0.0457 s.e. 0.1578 0.1567 0.1535 Coefficients for pi_ad: lag(oni_star,1) lag(pi_star,1) lag(hiato,1) lag(pi_ad,1) 0.0428 0.1015 0.6524 0.0423 s.e. 0.3108 0.0341 0.5917 0.1267 lag(oni_star,2) lag(pi_star,2) lag(hiato,2) lag(pi_ad,2) 0.3378 0.0510 -1.3854 -0.0541 s.e. 0.4479 0.0367 1.0199 0.1264 lag(oni_star,3) lag(pi_star,3) lag(hiato,3) lag(pi_ad,3) constant -0.1455 0.0303 0.8795 0.3049 1.1845 s.e. 0.3261 0.0360 0.5875 0.1206 0.6252 season().year2 season().year3 season().year4 -0.5070 -1.7955 0.3972 s.e. 0.7827 0.7770 0.7612 Residual covariance matrix: oni_star pi_star hiato pi_ad oni_star 0.6806 1.1047 -0.0131 -0.0714 pi_star 1.1047 55.4166 0.0012 3.8450 hiato -0.0131 0.0012 0.1630 0.0947 pi_ad -0.0714 3.8450 0.0947 4.0110 log likelihood = -519.71 AIC = 1199.42 AICc = -2040.58 BIC = 1386.92O gráfico abaixo sintetiza as contribuições dos fatores para a variável de interesse, a inflação de alimentos, sob a ótica da decomposição histórica dos choques estruturais do modelo VAR. No período de 2015-2016, o fenômeno El Niño contribuiu consideravelmente para o aumento da inflação. No período da pandemia, de 2019 até 2021, a variável climática contribuiu para o aumento da inflação de forma menos expressiva. E mais recentemente, no terceiro trimestre de 2023, a variável climática começou a contribuir para o aumento da inflação novamente, porém em magnitude inferior em relação a períodos anteriores.
Este artigo contribui marginalmente para a avaliação dos efeitos de impactos climáticos no desvio da trajetória de equilíbro da inflação de alimentos no Brasil no período atual.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Conclusão
Será que o El Niño impacta o preço do feijão com arroz no prato dos brasileiros? Para responder esta pergunta estimamos um modelo VAR(p) utilizando dados do Oceanic Niño Index (ONI) e investigamos a decomposição histórica dos choques estruturais.
Referências
BANCO CENTRAL DO BRASIL (2019). Impactos do clima na inflação de alimentos. Estudo Especial nº 57/2019.
