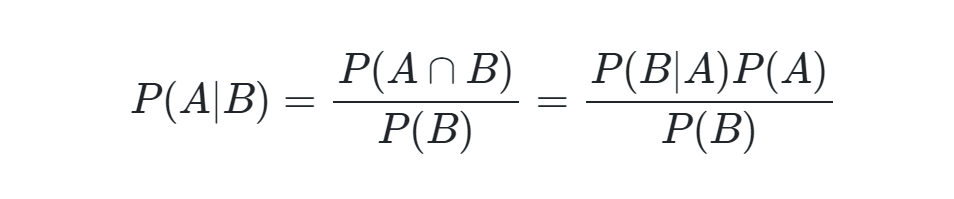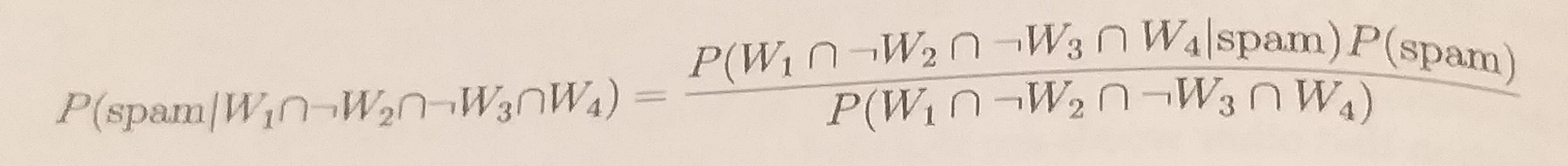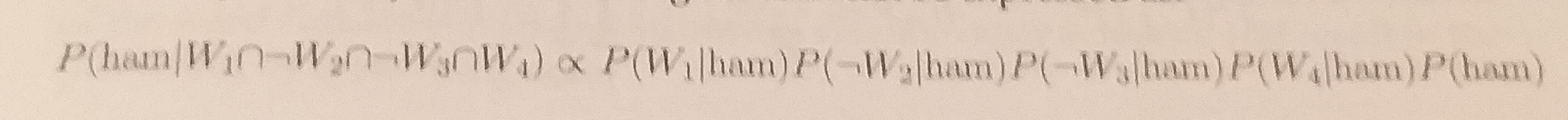Quando um meteorologista fornece uma previsão do tempo, ele em geral a descreve como “há 70% de chance de chover hoje”. Previsões do tempo estão baseadas em métodos probabilísticos, de modo a descrever eventos incertos. Utiliza-se eventos passados para extrapolar eventos futuros.
Uma previsão do tipo “70% de chance de chover” equivale a dizer que em 7 de 10 casos anteriores, com condições atmosféricas similares, choveu.
Neste artigo exploraremos:
- Princípios básicos de probabilidade;
- O modelo de classificação Naive Bayes;
- Como empregar o algoritmo Naive Bayes para lidar com comentários spam em redes sociais.
Este material é baseado, principalmente, no capítulo 4 de Lantz (2013).
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
Princípios básicos
Para começarmos, basta sabermos que probabilidade é um número entre 0 e 1, que captura as chances de um evento ocorrer, dado um conjunto de evidências.
O algoritmo Naive Bayes, como o próprio nome diz, está baseado no famoso Teorema de Bayes, que veremos daqui a pouco. Ele utiliza um conjunto de treino de modo a calcular a probabilidade de cada resultado com base nos valores de variáveis conhecidas. Assim, quando o algoritmo é aplicado a dados não rotulados, ele utiliza as probabilidades observadas para prever a qual classe mais provável pertence aquele dado.
Os algoritmos Naive Bayes podem ser utilizados em diversas situações, como por exemplo:
- Classificação de texto;
- Busca de intrusos ou anomalias em computadores;
- Diagnósticos médicos.
Tipicamente, classificadores bayesianos são melhor empregados em problemas onde a informação de inúmeros atributos deve ser considerada de forma simultânea de modo a estimar a probabilidade geral de um determinado resultado.
Enquanto muitos algoritmos de ML ignoram variáveis que tenham pouco efeito, métodos bayesianos utilizam toda a evidência disponível para mudar sutilmente as previsões. Se um número grande de variáveis possui efeitos relativos pequenos, o impacto conjunto pode ser bastante importante.
A teoria de probabilidade bayesiana está enraizada na ideia de que a probabilidade estimada de um evento, ou um potencial resultado, deveria ser baseada na evidência disponibilizada por várias tentativas (trial), ou oportunidades para que o evento ocorra.
Por exemplo, um trial para o evento candidato se torna presidente é uma eleição presidencial. Ou, para o evento uma mensagem é um spam, temos como trial uma mensagem de email recebida.
Métodos bayesianos proverão insights sobre como a probabilidade desses eventos pode ser estimada a partir de dados observados.
A probabilidade de um evento é estimada a partir dos dados observados, dividindo-se o números de tentativas onde o evento ocorreu pelo número total de tentativas. Por exemplo, se choveu em 3 dos 10 dias com condições atmosféricas similares, a probabilidade de chover hoje será de . De forma similar, se 10 dos 50 e-mails recebidos forem considerados como spam, a probabilidade de um email recebido ser um spam será de 20%.
Como consequência, a probabilidade de não chover será de 70% e a probabilidade de um email não ser um spam será de 80%. Isto porque, estamos tratando de eventos que são mutuamente exclusivos, i.e., não podem podem ocorrer ao mesmo tempo.
Sob certas circunstâncias, porém, podemos estar interessados em eventos não mutuamente exclusivos. Se certos eventos ocorrem com o evento de interesse, nós podemos usá-lo para fazer previsões.
Por exemplo, no caso do spam, um segundo evento pode ser e-mails contendo a palavra Viagra. Na maioria dos casos, essa palavra aparecerá em e-mails considerados como spam. Sua presença em um email recebido é uma forte evidência de que a mensagem em questão é um spam.
Nós sabemos que 20% de todas as mensagens são spam e 5% de todas as mensagens contêm a palavra Viagra. Estamos interessados, então, em definir a probabilidade de que e
ocorram ao mesmo tempo, isto é,
.
Calcular depende da probabilidade conjunta de dois eventos ou como a probabilidade de um evento está relacionada com a probabilidade de outro evento. Se dois eventos são totalmente não relacionados, eles são chamados de eventos independentes.
Os eventos podem ocorrer ao mesmo tempo, mas se eles são independentes significa dizer que saber a probabilidade de um evento ocorrer não provê qualquer informação sobre o outro evento.
Se todos os eventos são independentes, é impossível prever um observando outro. Em outras palavras, eventos dependentes são a base da modelagem preditiva.
Assim como a presença de nuvens é um preditor de um dia chuvoso, a presença da palavra Viagra é um preditor de um email spam. Isso dito, calcular a probabilidade de eventos dependentes é um pouco mais complexo do que a de eventos independentes. Se e
são independentes, nós podemos facilmente calcular
como sendo
, isto é, 1% de todas as mensagens serão spam com o termo Viagra.
De forma geral, para eventos independentes, teremos:
Nós sabemos, porém, que o cálculo acima está incorreto porque e
não são independentes.
O relacionamento entre eventos dependentes pode ser descrito utilizando o Teorema de Bayes:
Essa formulação provê um meio de pensar sobre como rever a probabilidade estimada de um evento à luz da evidência disponibilizada por outro evento. A notação deve ser lida como a probabilidade do evento A ocorrer, dada a ocorrência do evento B. Isso é conhecido como probabilidade condicional.
Dado que , podemos reescrever o Teorema de Bayes da seguinte forma:
Esse é o formato mais tradicional em que o teorema é apresentado.
De modo a entender como o teorema de Bayes funciona na prática, vamos revisitar nosso hipotético filtro de spam.
Sem termos conhecimento sobre o conteúdo de uma mensagem de email recebida, a melhor estimativa do seu spam status será , a probabilidade de que uma mensagem anterior (prior message) era um spam, que foi calculada como sendo 20%. Essa estimativa é conhecida como probabilidade prévia ou prior probability.
Suponha agora que você obteve evidência adicional ao olhar com mais cuidado o conjunto de mensagens recebidas de modo a verificar a frequência com que o termo Viagra aparece. A probabilidade do termo Viagra ser utilizado em mensagens consideradas como spam anteriormente será , sendo conhecida simplesmente como probabilidade ou likelihood.
A probabilidade de que o termo Viagra apareça em qualquer mensagem, ou será então conhecida como probabilidade marginal ou marginal likelihood.
Ao aplicar o teorema de Bayes sobre essa evidência, nós poderemos computar a probabilidade posterior ou posterior probability que irá medir a probabilidade de uma mensagem ser spam. Assim, se a probabilidade posterior for maior do que 50%, é mais provável que a mensagem seja considerada um spam do que uma mensagem verdadeira, sendo então filtrada.
De modo a calcular os componentes da figura acima, é conveniente construir uma tabela de frequências, que mede o número de vezes que o termo Viagra aparece em mensagens spam e mensagens normais. A partir dessa tabela, podemos construir uma tabela de probabilidades. As tabelas abaixo ilustram.
Tabela de frequência:
| Classificação | Sim | Não | Total |
|---|---|---|---|
| Spam | 4 | 16 | 20 |
| Não Spam | 1 | 79 | 80 |
| Total | 5 | 95 | 100 |
Tabela de probabilidades:
| Classificação | Sim | Não | Total |
|---|---|---|---|
| Spam | 4/20 | 16/20 | 20/100 |
| Não Spam | 1/80 | 79/80 | 80/100 |
| Total | 5/100 | 95/100 | 100 |
A tabela de probabilidades revela que , indicando que a probabilidade de que uma mensagem contenha o termo Viagra, dado que ela é spam, será de 20%.
Ademais, dado que , nós podemos calcular
como sendo
=
, o que é totalmente diferente da estimativa que obtivemos supondo independência de eventos.
Para computar a probabilidade posterior, , nós tomamos
ou
. Assim, há uma probabilidade de 80% que a mensagem seja spam, se ela contém o termo Viagra. Com efeito, qualquer mensagem que contiver o termo Viagra deve ser filtrada.
É basicamente assim que um filtro de spam funciona, considerando obviamente um número muito maior de termos de forma simultânea.
O algoritmo Naive Bayes
O algoritmo Naive Bayes descreve um método simples de aplicar o teorema de Bayes a problemas de classificação. Embora não seja o único método de ML a utilizar métodos bayesianos, é o mais comum. Em particular, para classificação de textos. Entre os pontos fortes desse método, estão:
- Ele é simples, rápido e bastante efetivo
- Trabalha bem com ruídos e valores faltantes
- Requer poucos exemplos para treino, trabalhando bem também com muitos exemplos
- Fácil obtenção da probabilidade estimada para previsão
A seguir, algumas de suas limitações:
- Baseia-se numa suposição frequentemente defeituosa de características igualmente importantes e independentes
- Não é ideal para conjuntos de dados com muitas variáveis numéricas
- As probabilidades estimadas são menos confiáveis do que as classes preditas
O algoritmo Naive Bayes recebe essa determinação “naive” por suas premissas ingênuas em relação aos dados. Em particular, ele assume que as variáveis do conjunto de dados são igualmente importantes e independentes. Essa premissa é raramente válida para a maioria dos casos.
No nosso exemplo do spam, é quase certo que algumas variáveis serão mais importantes do que outras. Por exemplo, o remetente do e-mail será provavelmente mais importante do que propriamente o texto da mensagem.
A despeito disso, mesmo quando a premissa é violada, o algoritmo performa bastante bem.
Vamos, então, estender nosso filtro de spam ao adicionar outros termos a serem monitorados. Além do termo Viagra, vamos considerar Money, Groceries e Unsubscribe.
Ao receber uma mensagem, nós devemos calcular a probabilidade posterior para determinar se a mensagem é um spam ou email normal, dada a possibilidade dos termos encontrados no texto da mensagem.
Por exemplo, suponha que a mensagem contenha os termos Viagra e Unsubscribe, mas não contenha Money ou Groceries. Usando o teorema de Bayes, nós podemos definir o problema como na fórmula abaixo. Ela captura a probabilidade da mensagem ser spam, dado .
Por diversas razões, essa fórmula é computacionalmente difícil de ser resolvida. À medida que outros termos são adicionados, será necessário uma quantidade absurda de memória para guardar as probabilidades para todas as possibilidades.
O trabalho se tornará mais fácil se nós explorarmos o fato do teorema assumir independência entre eventos. Especificamente, ele assume independência condicional de classe, o que significa que os eventos são independentes à medida em que eles são condicionados ao mesmo valor de classe. Ao assumir essa propriedade, podemos simplificar a fórmula usando a regra de probabilidade para eventos independentes.
Assim, a probabilidade condicional da mensagem ser spam pode ser expressa como:
E a probabilidade de ser uma mensagem normal:
O símbolo utilizado é o “proporcional a”, ressaltando que o denominador foi omitido. Assim, utilizando os valores da tabela de probabilidades, podemos a probabilidade do email ser spam como
E a probabilidade de ser uma mensagem comum:
Dado que , nós podemos dizer que é 6x mais provável que a mensagem seja um spam. Para transformar esse número em probabilidades, nós devemos fazer
.Nós podemos generalizar o algoritmo de classificação Naive Bayes a partir da seguinte fórmula:
Isto é, a probabilidade do nível da classe
, dadas as evidências providas pelos recursos
será igual aos produtos das probabilidades de cada pedaço de evidência condicionada aos níveis das classes, a probabilidade anterior do nível da classe e um fator
, que converte os valores de possibilidades para probabilidades.
O estimador Laplace
Antes de aplicar o algoritmo Naive Bayes em problemas mais complexos, há algumas nuances a serem consideradas. Suponha que nós recebamos outra mensagem contendo todos os quatro termos. Nós calculamos a probabilidade de ser spam como
Enquanto a probabilidade de ser um email normal será:
Assim, a probabilidade de ser spam será .
Uma solução para esse problema envolve usar algo chamado como estimador Laplace. O estimador basicamente adiciona um pequeno número a cada uma das contagens na tabela de frequências, o que assegura que cada uma delas será diferente de zero. Usando o estimador com valor igual a 1 para o nosso exemplo, teríamos:
e
Exemplo de classificação textual com dados reais
Agora iremos brevemente descrever a aplicação do modelo Naive Bayes para um problema de classificação com dados reais.
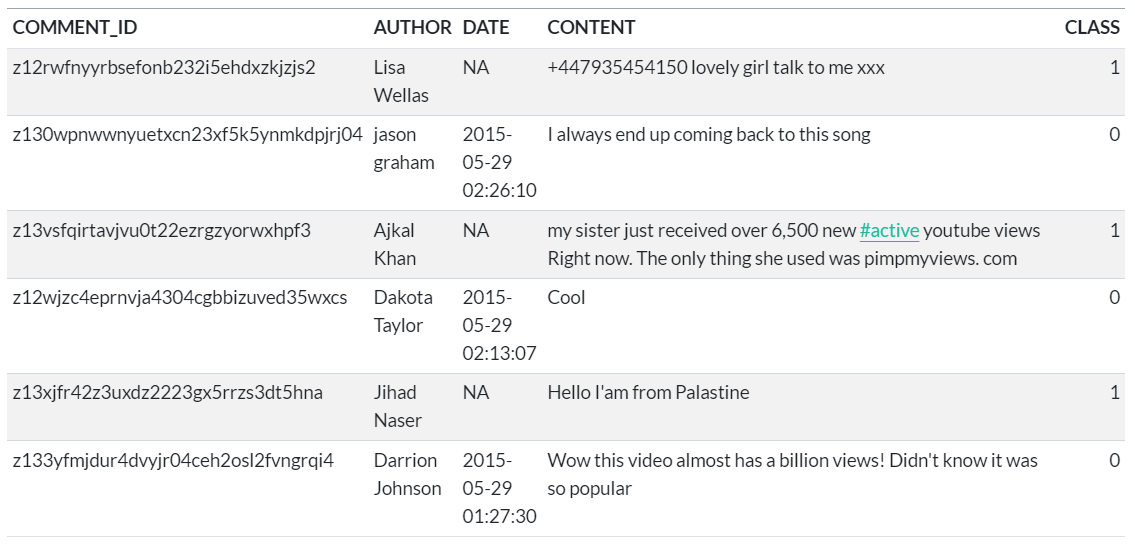
O objetivo é classificar comentários de um vídeo no YouTube como “spam” ou “não spam”. O vídeo foi publicado na plataforma em 2010 e está intitulado como “Eminem - Love The Way You Lie ft. Rihanna”. Os comentários (uma amostra) estão armazenados no conjunto de dados YouTube Spam Collection (arquivo Youtube04-Eminem.csv) e apresentam estrutura de dados textual.
A tabela abaixo mostra as primeiras linhas da tabela de dados brutos:
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
A coluna CLASS é a variável de interesse, ou seja, o objetivo é classificar as categorias presentes na coluna. A origem da classificação presente na tabela acima é desconhecida.
A partir dos dados brutos, diversos procedimentos de processamento de dados textuais são aplicados (capitalização da fonte, remoção de números/stop words/pontuação, processamento de stemming, separação aleatória de amostras de treino e teste, remoção de termos infrequentes, etc.). Códigos relacionados a estes procedimentos são omitidos aqui por brevidade.
A tabela abaixo mostra a estrutura da tabela de dados processados (treino):
Agora que os dados estão em um formato que pode ser representado por um modelo estatístico, podemos aplicar o algoritmo Naive Bayes. O algoritmo usará a contagem de termos relevantes para estimar a probabilidade de que um dado comentário seja um spam.
O código abaixo se encarrega de estimar o modelo, produzir previsões para a amostra de teste e reportar estatísticas de acurácia:
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Matriz de confusão: [[158 0] [ 7 196]] Acurácia: 0.9806094182825484
Conclusão
Neste artigo apresentamos o modelo Naive Bayes para problemas de classificação binária. Mostramos a intuição do modelo e sua formulação matemática, além de pontuar as principais aplicações e casos de uso. Ao final, demonstramos um exemplo aplicado à classificação de spam em comentários do YouTube, usando as linguagens de programação R e Python.
Referências
Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, fale com a gente no Whatsapp e veja como fazer parte do Clube AM, clicando aqui.