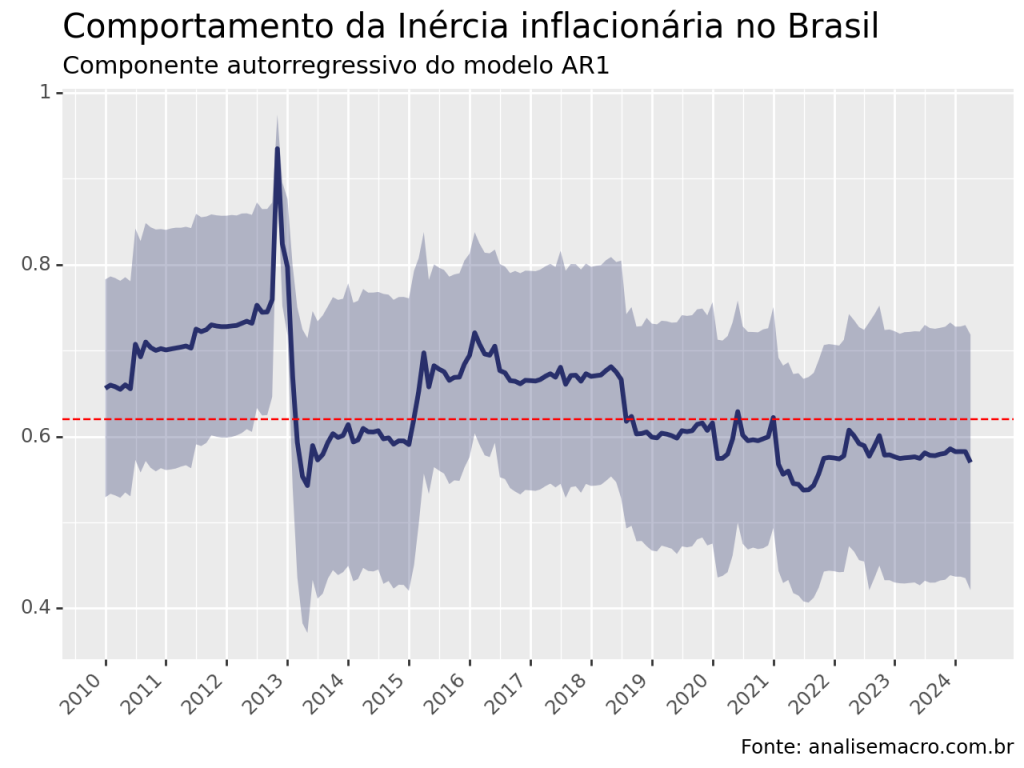
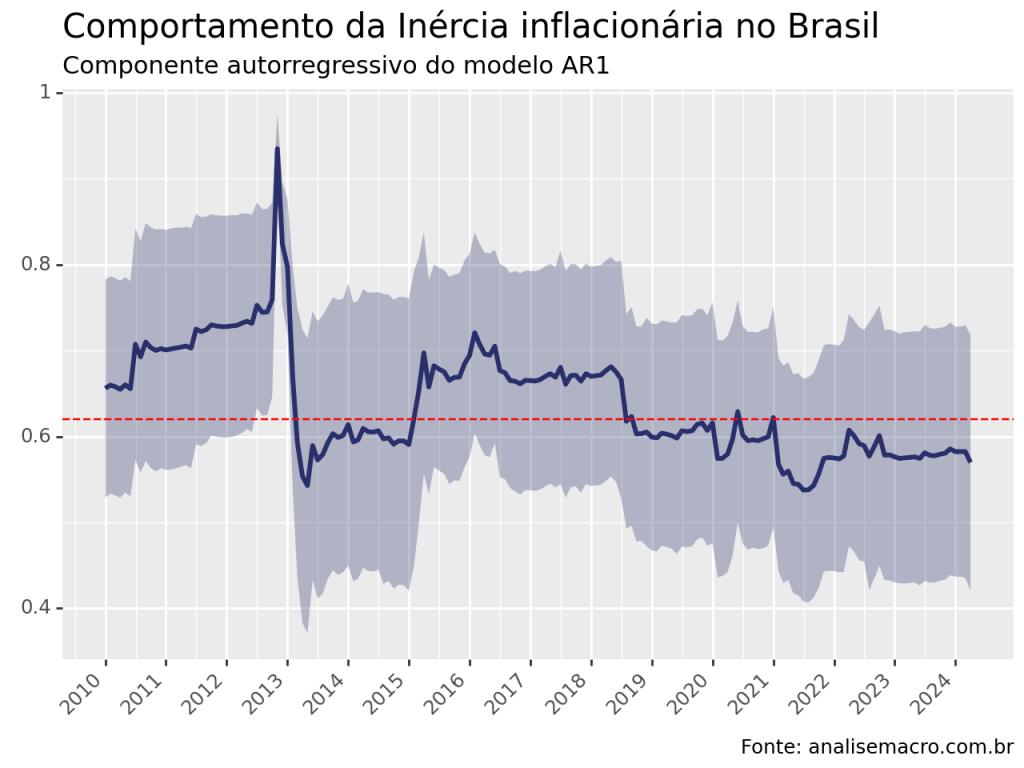
Estimando a Inércia Inflacionária usando o Python

Como que a inflação passada pode afetar a inflação presente? É possível mensurar esse efeito, isto é, o grau de persistência da inflação, por meio de um processo autorregressivo de ordem 1. Mostramos como construí-la utilizando o Python como ferramenta de coleta de dados, análise e ajuste do modelo.

Inércia ou simplesmente persistência não é exclusividade do processo inflacionário. Em uma leitura econométrica, pode-se dizer que a maior parte das variáveis macroeconômicas possui algum grau de persistência, ilustrado por uma autorregressividade positiva. Em outras palavras, se uma variável macroeconômica qualquer puder ser descrita por um processo autorregressivo de ordem um, como em

$\begin{align*} y_t = \alpha y_{t-1} + \varepsilon_t \end{align*}$

onde $\alpha > 0$ , então diz-se que a variável em questão apresenta algum grau de persistência. E o grau aqui é de suma importância. Isso porque, como sabemos do estudo de séries temporais, se $\alpha$ estiver no intervalo aberto entre 0 e 1, o processo autorregressivo é dito estacionário.

Nesse caso, mesmo que haja um grau elevado de persistência (isto é, $\alpha$ está mais próximo de 1), choques de oferta gerarão efeito, mas se dissiparão ao longo do tempo. Contudo, se $\alpha$ for maior ou igual a 1, a série passa a não ser mais estacionária, o que implica em desvio permanente na ocorrência de um determinado choque sobre a variável em questão.

Isso dito, parece razoável supor que o coeficiente $\alpha$ em 1 nos dará o grau de persistência, para qualquer variável macroeconômica ou de inércia, no caso específico da inflação.

No Python, é possível identificar a inércia inflacionário construindo um código que permita estimar o AR1 em uma janela de tempo, isto é, criar um rolling ARIMA(1,0,0) utilizando a biblioteca statsmodels.

Abaixo, ilustramos o resultado encontrado, tomando como base a variação mensal do IPCA, identificada pelo código 433 no Sistema Gerenciador de Séries Temporais, no período de janeiro de 2000 até abril de 2024. O modelo estimado utiliza uma amostra de 120 meses.

_____________________________________

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Devemos usar a métrica MAPE em previsão de demanda?

Regimes inflacionários com Modelo Oculto de Markov usando Python

Regimes da Política Monetária Brasileira com Markov Switching no Python

Como criar janelas móveis de séries temporais usando o Python

Como incorporar choques em cenários de previsão?

Como preparar os dados para um modelo preditivo?

Outros artigos relacionados

Devemos usar a métrica MAPE em previsão de demanda?

A previsão de demanda é um componente essencial da análise econômica e empresarial. Para avaliar a precisão das previsões, diversas métricas de erro são utilizadas. Entre elas, o Erro Percentual Absoluto Médio (MAPE - Mean Absolute Percentage Error) é uma das mais conhecidas. Neste artigo discutimos suas vantagens e desvantagens com exemplos.

Regimes inflacionários com Modelo Oculto de Markov usando Python

Neste exercício, utilizamos Python para aplicar um Modelo Oculto de Markov (HMM) na identificação e análise de regimes inflacionários no Brasil, com base na série temporal do IPCA mensal.

Regimes da Política Monetária Brasileira com Markov Switching no Python

Este exercício analisa a política monetária brasileira utilizando modelos de Markov Switching Regression. O objetivo é identificar diferentes regimes de política monetária e como eles influenciam a taxa Selic, a meta de inflação e o hiato do produto. Usamos a linguagem de programação Python para o processo de coleta, tratamento, análise e modelagem dos dados.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!