Como melhorar o processo de alocação de peso em um portfólio de investimentos? Veremos como realizar a aplicação do Hierarchical Risk Parity (HRP) no Python.
- Exige a estimativa de retornos esperados.
- Exige a estimativa e, mais importante, a inversão de uma matriz de covariância positiva definida.
O primeiro problema deu origem a um aumento no uso de estratégias de otimização baseadas em risco, como risk budgeting e risk parity. Estudos demonstraram que a estimativa de retornos esperados tem um impacto maior na instabilidade do portfólio do que a estimativa da matriz de covariância.
Apesar de as estratégias de alocação baseadas em risco não dependerem da estimativa de retornos esperados, elas ainda requerem a inversão de uma matriz de covariância potencialmente mal condicionada. Geralmente, a matriz de covariância é mal condicionada quando os ativos são altamente correlacionados, implicando um alto número de condição. A inversão de uma matriz mal condicionada muitas vezes resulta na amplificação de erros inerentes à estimativa e, em última análise, resulta em um portfólio numericamente instável, conhecido como a “Markowitz Curse”.
Devido à falta de confiabilidade e ao desempenho insatisfatório tanto do portfólio de média-variância de Markowitz quanto de outras estratégias de otimização baseadas em risco, muitas pesquisas têm se concentrado em estratégias para melhorar a robustez e reduzir a instabilidade numérica da matriz de covariância.
Em 2016, Lopéz de Prado introduziu uma nova estratégia de alocação de ativos na tentativa de contornar as falhas inerentes das estratégias tradicionais de otimização. A abordagem Hierarchical Risk Parity (HRP) apresentada combina a hierarquização de ativos com uma estratégia heurística de alocação baseada em risco, com o objetivo de tornar a alocação mais ótima. Em resumo, a abordagem opera em três etapas:
- Os ativos são agrupados com base em correlações entre pares para formar uma árvore.
- Os ativos são rearranjados de acordo com a estrutura da árvore para formar uma matriz de covariância quase diagonal.
- As alocações são divididas entre subconjuntos de ativos usando alocação inversa de variância.
Na prática, o HRP não requer a previsão de retornos nem a inversão da matriz de covariância. Como resultado, a abordagem visa não apenas lidar com a instabilidade do portfólio construído, mas também melhorar o desempenho e reduzir a concentração.
Clustering
A análise de agrupamento, ou clustering, é uma técnica de aprendizado não supervisionado na qual um algoritmo organiza dados não rotulados em grupos ou clusters com base em características semelhantes. O objetivo é descobrir padrões naturais nos dados, agrupando instâncias que compartilham características comuns. Diferentemente do aprendizado supervisionado, onde o algoritmo é treinado com dados rotulados para realizar tarefas específicas, o aprendizado não supervisionado não depende de rótulos prévios e busca encontrar estruturas subjacentes nos dados de forma independente.
Mais especificamente, o agrupamento é o processo de agrupar uma coleção de objetos em clusters com base em um conjunto selecionado de características associadas a esses objetos. O agrupamento pode ser usado para diferentes propósitos, mas o objetivo geral é dividir objetos em clusters de tal maneira que objetos semelhantes sejam colocados no mesmo cluster, enquanto objetos dissimilares são colocados em clusters diferentes. O grau de semelhança entre dois objetos é determinado em relação às características dos objetos e a uma definição formal de semelhança ou dissimilaridade. A dissimilaridade entre dois objetos muitas vezes é medida de distância, como a distância euclidiana ao quadrado entre os vetores de características dos dois objetos. O quanto uma medida de distância é apropriada depende em grande parte dos dados e do objetivo. Por exemplo, pode fazer menos sentido usar a distância euclidiana ao quadrado como medida de dissimilaridade para características não quantitativas.
Além disso, o agrupamento pode ser dividido em duas classes principais - agrupamento particional e agrupamento hierárquico. O agrupamento particional cria uma partição de nível único dos objetos, e os métodos mais comuns são k-means e k-medoids. O agrupamento hierárquico, por outro lado, cria uma hierarquia de múltiplas partições binárias. Como o agrupamento hierárquico é um dos principais elementos desta tese, a próxima seção é dedicada a uma descrição mais elaborada do tópico.
Hierarchical Clustering
O Hierarchical Clustering classifica dados em clusters binários aninhados, resultando em uma estrutura hierárquica ou árvore. Uma vantagem do Hierarchical Clustering é sua consideração pelas estruturas hierárquicas claras que podem existir em sistemas complexos, como os mercados financeiros, influenciando fortemente a dinâmica desses sistemas. O clustering hierárquico oferece uma descrição quantitativa dessas hierarquias, contribuindo para uma modelagem mais adequada de um sistema.
No entanto, o Hierarchical Clustering requer que os objetos a serem classificados tenham medidas numéricas em um conjunto de características. Cada objeto tem seu próprio vetor de características, que conjuntamente constituem a matriz de características, onde cada linha corresponde a um objeto e cada coluna corresponde a uma característica. A análise é subsequentemente realizada nas linhas desta matriz. As características são usadas para calcular as distâncias entre os objetos, que servem como base para o agrupamento - objetos com características semelhantes são agrupados, e objetos com características diferentes são colocados em clusters diferentes.
No contexto da construção de portfólio, a matriz de correlação pode servir como base para a análise, onde cada ativo representa um objeto e as características podem ser definidas como uma função das correlações par a par entre os ativos. Além disso, o clustering hierárquico pode ser descrito em termos de dois passos principais: (1) estruturar os dados para representar a distância entre os objetos e (2) realizar o agrupamento e introduzir a hierarquia. O primeiro passo envolve a escolha de uma medida de distância adequada e a avaliação dos dados com base nessa medida, geralmente envolvendo o cálculo das distâncias entre os vetores de características. O segundo passo consiste em formar os clusters com base nas distâncias determinadas no primeiro passo e em algum critério de ligação, que define a distância entre os clusters.
Por fim, vale mencionar que existem dois tipos principais de clustering hierárquico - aglomerativo e divisivo. O clustering aglomerativo é comumente descrito como uma abordagem ascendente, enquanto o clustering divisivo é uma abordagem descendente. Em cada iteração, dois clusters são combinados, reduzindo o número de clusters em um a cada iteração até restar apenas um cluster. Na última iteração, a raiz da árvore é formada. A decisão de quais clusters combinar em cada iteração é determinada pelas distâncias entre os clusters presentes nessa iteração, geralmente combinando os dois clusters com a menor distância entre eles. No entanto, diferentes critérios de ligação definem as distâncias entre os clusters de maneiras diversas, resultando em árvores muito diferentes.
Construção de Portfólio com Hierarchical Clustering
A construção de portfólio utilizando o algoritmo de Hierarchical Clustering envolve um processo intricado dividido em três etapas fundamentais, cada uma desempenhando um papel crucial na otimização do portfólio:
1. Hierarchical Clustering
O primeiro passo envolve a aplicação do Hierarchical Clustering, uma técnica que agrupa ativos financeiros com base em padrões identificados nos dados históricos. Este algoritmo forma clusters que encapsulam ativos com características semelhantes, promovendo a criação de grupos que compartilham uma afinidade específica. A visualização desse agrupamento é frequentemente facilitada através de um dendrograma, uma representação gráfica que ilustra as relações hierárquicas entre os clusters.
Este estágio é crucial para a identificação de conjuntos de ativos que exibem comportamentos similares ao longo do tempo, permitindo a construção de um portfólio mais diversificado e equilibrado. Usualmente, existem 4 algortimos que podem ser aplicados, cada um com sua função (não iremos entrar em detalhes)
- (Default) Single linkage
- Complete linkage
- Average linkage
- Ward’s linkage
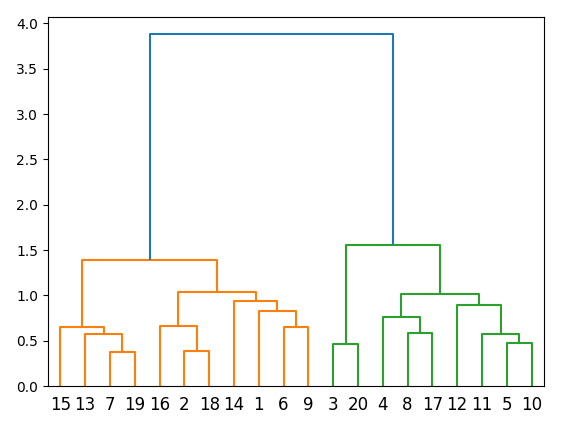
O dendograma de exemplo abaixo pode ajudar a entender o processo de agrupamento.
2. Quasi-Diagonalization
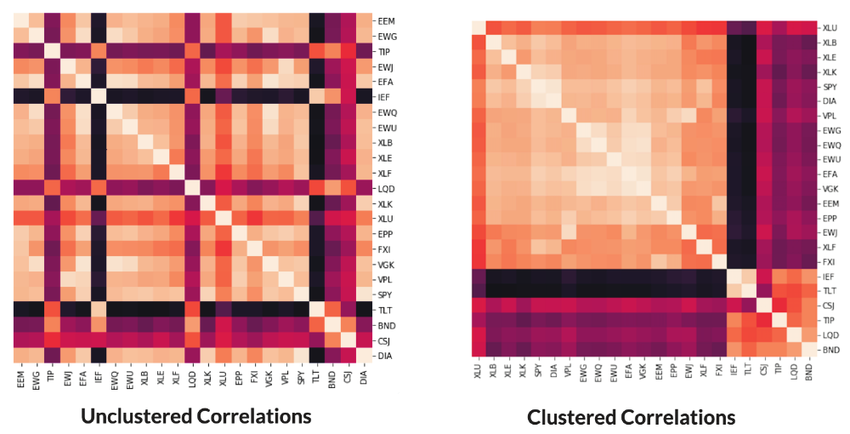
A etapa subsequente, conhecida como Quasi-Diagonalization, incide sobre a reorganização da matriz de covariância dos ativos. Nesse processo, as linhas e colunas da matriz são rearranjadas de modo a reunir ativos com características semelhantes, enquanto aqueles com comportamentos distintos são separados. Esta reorganização efetua uma espécie de “diagonalização aproximada”, favorecendo uma representação visual que evidencia a proximidade entre ativos similares. Uma representação gráfica, como um diagrama, pode oferecer uma visão clara dessa reorganização.
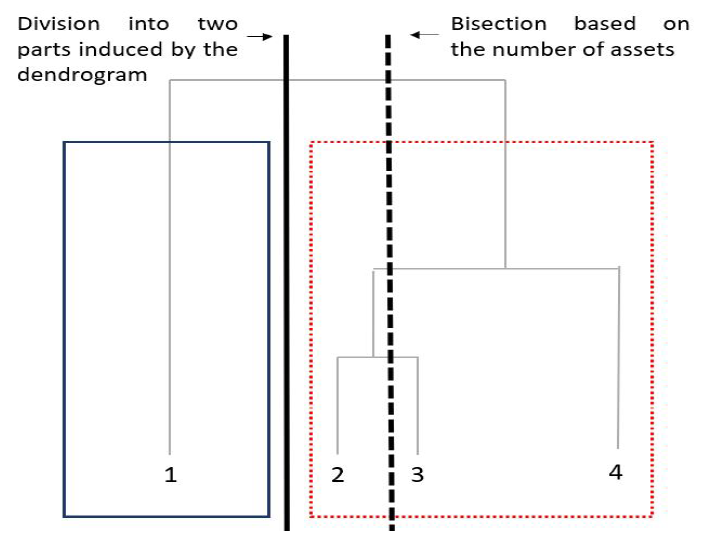
3. Recursive Bisection
A terceira etapa, conhecida como Recursive Bisection, atribui pesos ao portfólio de forma ascendente e recursiva, desdobrando os clusters hierárquicos formados anteriormente. Cada cluster é subdividido em sub-clusters, começando com um cluster maior e descendendo na árvore hierárquica. Esse processo faz uso da matriz quasi-diagonalizada, partindo do pressuposto de que, para uma matriz diagonal, a alocação de inverso-variância é a alocação mais otimizada.
Essa abordagem progressiva permite uma alocação eficiente de pesos no portfólio, adaptando-se dinamicamente às mudanças nas características e comportamentos dos ativos ao longo do tempo. No entanto, é essencial ressaltar que, como em qualquer estratégia de construção de portfólio, a interpretação cuidadosa dos resultados e a compreensão das nuances do mercado são cruciais para o sucesso dessa abordagem.
Alunos inscritos no curso de Mercado Financeiro e Gestão de Portfólio com o Python têm a oportunidade de adquirir conhecimento em todas as etapas a seguir, além de obter uma compreensão teórica abrangente das principais ferramentas utilizadas no Mercado Financeiro.
Exemplo no Python
Para construir o HRP no Python, podemos ter como auxilio a biblioteca riskfolio, que permite utilizar diversos algoritmos de otimização de portfólio. Usamos dados dos seguintes tickers: 'AAPL', "AMZN", 'ITSA4.SA', 'BBDC4.SA' no período de 2018 até o fim de 2022.
O primeiro passo é o de calcular o retorno (diário) dos ativos, como abaixo:
Código
| AAPL | AMZN | ITSA4.SA | BBDC4.SA | |
|---|---|---|---|---|
| Date | ||||
| 2018-01-03 | -0.0174% | 1.2775% | 0.4598% | 1.1786% |
| 2018-01-04 | 0.4645% | 0.4476% | 1.6407% | 1.8818% |
| 2018-01-05 | 1.1386% | 1.6163% | 0.5665% | 0.1759% |
| 2018-01-08 | -0.3714% | 1.4425% | -0.0282% | -0.0878% |
| 2018-01-09 | -0.0115% | 0.4676% | -0.9296% | -1.5817%
|
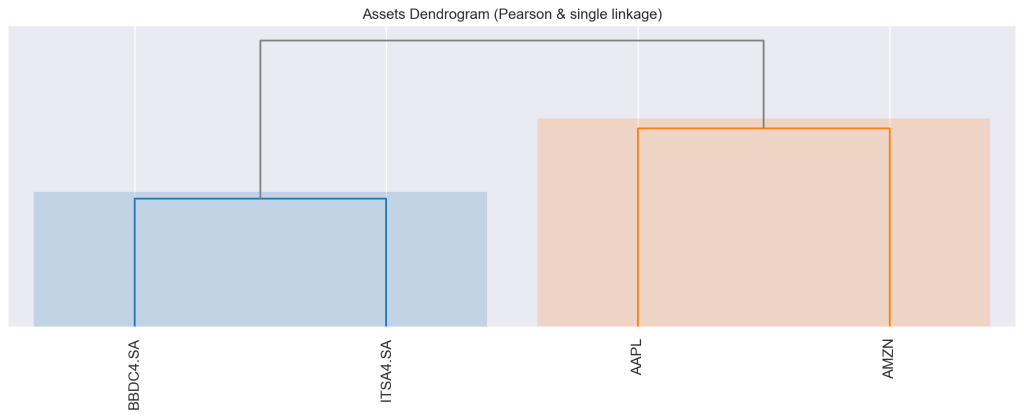
Em seguida, construímos o Dendograma, de forma a verificar o agrupamento. Veja que empresas brasileiras e norte-americanas são separadas.
Estimando o HRP Portfolio
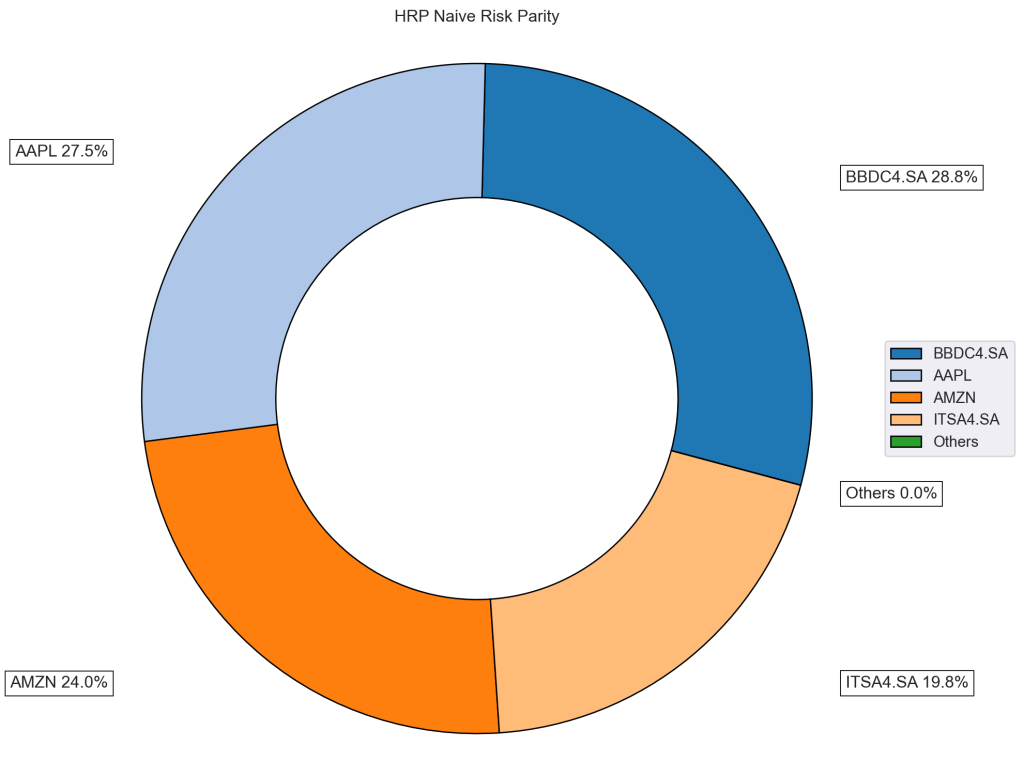
Facilmente obtemos os pesos ótimos criados pelo algortimo. Perceba que não há concentração em um único ativo, bem como as empresas norte-americanas possuem um peso maior.
Código
| AAPL | AMZN | ITSA4.SA | BBDC4.SA | |
|---|---|---|---|---|
| weights | 27.4505% | 24.0130% | 19.7672% | 28.7693% |
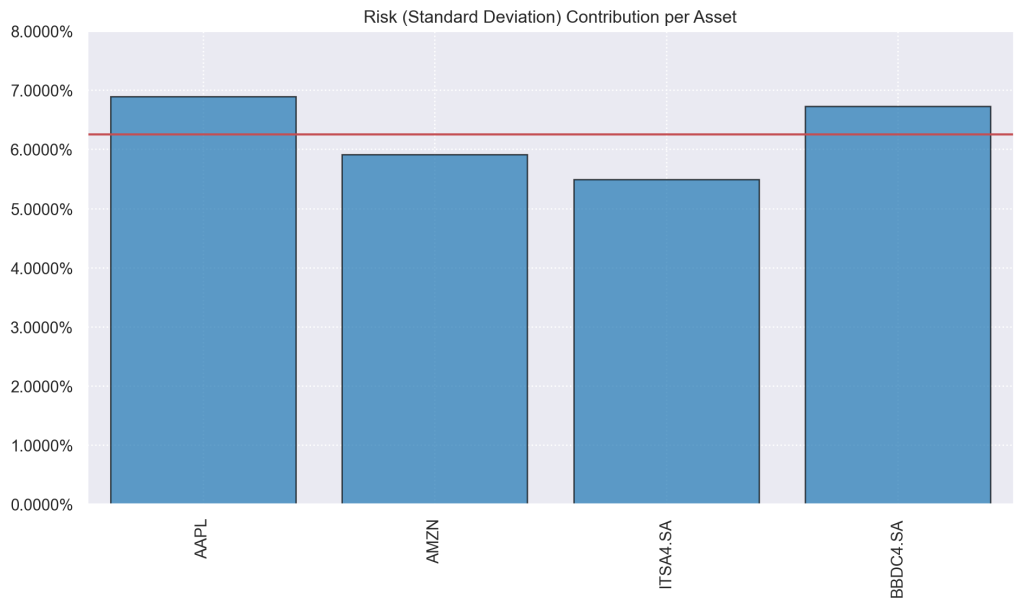
A composição pode ser facilmente visualizada.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Referências
Pál, László (2022). Asset Allocation Strategies Using Covariance Matrix Estimators. Acta Universitatis Sapientiae Economics and Business
Nanakorn, N., & Palmgren, E. (2021). Hierarchical Clustering in Risk-Based Portfolio Construction (Dissertation). Retrieved from https://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-304668
M. Lopéz de Prado. Building diversified portfolios that outperform out of sample. The Journal of Portfolio Management, 42(4):56–69, 2016.