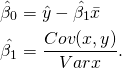[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Abel||||" text_font_size="21" use_border_color="off" border_color="#ffffff" border_style="solid"]
A turma de setembro do nosso Curso de Introdução à Econometria usando o R terá uma grande novidade. A apostila e as listas de exercício foram revisadas e atualizadas com exercícios do livro clássico de Jeffrey Marc Wooldridge. Todos feitos no R, de modo a mostrar para o aluno como a teoria pode ser complementada com a prática. Com isso, trazemos ainda mais aplicações para o curso, o que garante total absorção do conteúdo. Para ilustrar, vamos considerar nesse post o modelo de regressão simples. Primeiro, um pouco de teoria e depois um exemplo do Wooldridge feito no R.
[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2018/08/postsetembro.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Abel||||" text_font_size="21" use_border_color="off" border_color="#ffffff" border_style="solid"]
Estamos interessados em estimar os parâmetros populacionais e
de um modelo de regressão simples
(1)
a partir de uma amostra aleatória de e
. De acordo com Wooldridge, os estimadores de Mínimos Quadrados Ordinários (MQO) serão
(2)
Baseado nos parâmetros estimados, a reta de regressão será
(3)
Para uma dada amostra, nós precisaremos calcular as quatro estatísticas ,
,
e
e colocá-las nessas equações. Para ilustrar, vamos considerar o exemplo 2.3 do Wooldridge sobre Salários de CEOs e Retornos sobre o patrimônio. Para isso, considere o seguinte modelo
(4)
onde é o salário anual de CEO em milhares de dólares e
é o retorno médio sobre o patrimônio em percentual. O parâmetro
irá medir a variação no salário anual quando o retorno médio sobre o patrimônio aumentar em um ponto percentual. Para estimar esse modelo, podemos utilizar o conjunto de dados ceosal1.
data(ceosal1, package='wooldridge') attach(ceosal1)
Uma vez que tenhamos carregado o conjunto de dados, podemos calcular manualmente os parâmetros e
, como abaixo.
# Cálculo manual dos parâmetros b1hat = cov(roe,salary)/var(roe) b1hat b0hat = mean(salary) - b1hat*mean(roe) b0hat
Isto é, a reta de regressão será dada por
(5)
Implicando que para um , teremos um salário previsto de US$ 963.19, que é o intercepto. Ademais, se
= 1, então
= US$ 18.50. Podemos, por fim, desenhar a reta de regressão com o código abaixo.
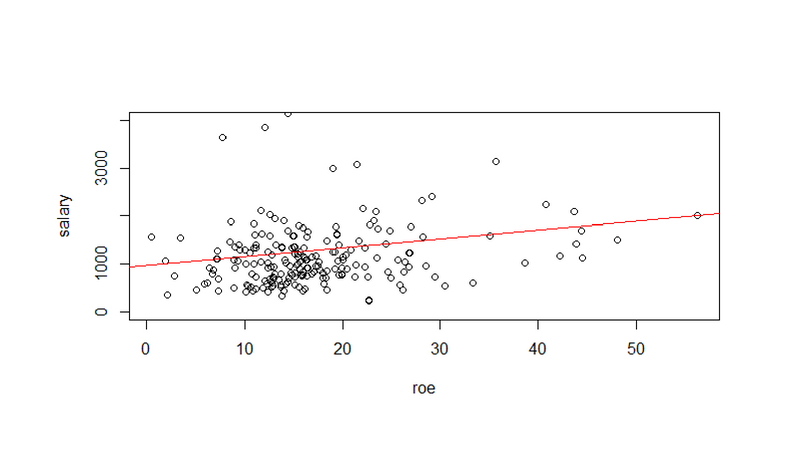
CEOregress = lm(salary ~ roe) plot(roe, salary, ylim=c(0,4000)) abline(CEOregress, col='red')
E o resultado...
[/et_pb_text][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2018/08/coversetembro.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/" url_new_window="off" use_overlay="off" animation="off" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][/et_pb_row][/et_pb_section]