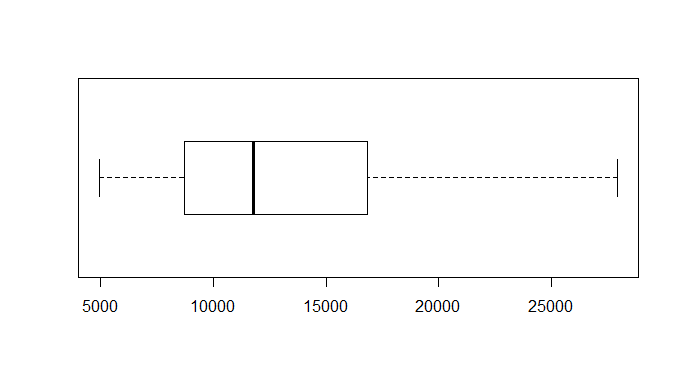Empresas grandes ou pequenas sempre estão interessadas em gerar alguma previsibilidade sobre seu faturamento. O problema básico de um empreendimento desses é a ausência de variáveis preditoras. Apenas em poucos casos, teremos variáveis em uma frequência adequada que conseguem explicar o faturamento de uma empresa. Pode ser interessante, portanto, utilizar modelos univariados, onde a nossa variável de interesse pode ser explicada pelas suas próprias defasagens. Para ilustrar, considere que um processo autorregressivo de ordem pode ser representado como
(1)
Ou, alternativamente, utilizando o operador defasagem como
(2)
Ou ainda em notação polinomial
(3)
Onde . Considerando, assim, um processo AR(1), como
(4)
teremos um ruído branco quando , um passeio aleatório quando
e
ou, quando
, um \emph{passeio aleatório com drift}. Analogamente, podemos representar um processo de média móvel MA(q) como
(5)
Ou, alternativamente, utilizando o operador defasagem, como
(6)
Ou ainda em notação polinomial
(7)
Utilizando o mesmo código acima, a propósito, podemos gerar alguns processos MA(1), modificando apenas o valor de . Ademais, como vimos, podemos combinar as equações 1 e 5, construindo assim um processo
, que pode ser representado como
(8)
Onde, novamente, . Alternativamente, utilizando o operador defasagem
(9)
Ou ainda, em notação polinomial
(10)
Por suposto, podemos, enfim, generalizar nossa análise para um modelo , onde
será a ordem de integração do processo, como vimos na seção anterior. Ele pode ser representado em termos de notação polinomial como
(11)
A equação 11 faz referência aos modelos ARIMA não sazonais. Os modelos ARIMA também são capazes de modelar uma ampla gama de dados sazonais. Um modelo ARIMA sazonal é formado pela inclusão de termos sazonais adicionais, na forma , onde o segundo componente faz referência à parte sazonal e
significa o número de períodos por estação. Em termos formais,
(12)
Uma vez que tenhamos chegado a modelos representados pela equação 11 e pela equação 12, podemos agora assim apresentar a metodologia proposta por Box et al. (2016). Ela consiste, basicamente, nos seguintes passos:
- Identificação: uso dos dados e de qualquer outra informação sobre como as séries foram geradas para construir um modelo univariado;
- Estimação: uso dos dados para construir inferências sobre os parâmetros condicionadas à adequação do modelo escolhido;
- Diagnóstico: Avaliar o quão bem o modelo estimado se adequa aos dados efetivamente observados;
- Previsão: Uma vez escolhido o melhor modelo, passa-se à etapa de previsão.
Para ilustrar, vamos considerar o faturamento de uma empresa específica. Nosso objetivo é construir um modelo SARIMA e a partir dele gerar previsões para os próximos 12 meses. Para começar, nós carregamos os seguintes pacotes:
library(tidyverse) library(ggplot2) library(forecast) library(scales) library(xtable)
Uma vez carregados os pacotes, podemos importar os dados de faturamento com o código a seguir:
data = read_csv2('data.csv',
col_types = list(col_date(format='%d/%m/%Y'),
col_integer()))
Uma vez que tenhamos importados os dados, podemos utilizar o pacote ggplot2 para visualizar a nossa variável de interesse.
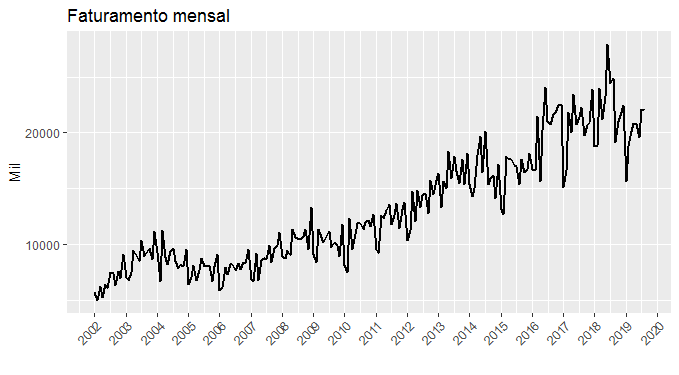
ggplot(data, aes(date, faturamento))+ geom_line(size=.8)+ scale_x_date(breaks='1 year', date_labels = '%Y')+ theme(axis.text.x=element_text(angle=45, hjust=1))+ labs(x='', y='Mil', title='Faturamento mensal')
Ao observar o gráfico, vemos que existe uma tendência positiva associada ao faturamento da empresa, configurando a nossa série como não estacionária. Em outras palavras, de modo a modelar a nossa série, um primeiro passo é torná-la estacionária. A seguir, um plotamos um boxplot da série.
A mediana da série é de R$ 11.766 mil, o 1º quartil termina em R$ 8.729 mil e o terceiro quartil em R$ 16.807 mil. O IQR da série é, portanto, de R$ 8.077,25 mil. A seguir, verificamos se a série em questão apresenta alguma sazonalidade.
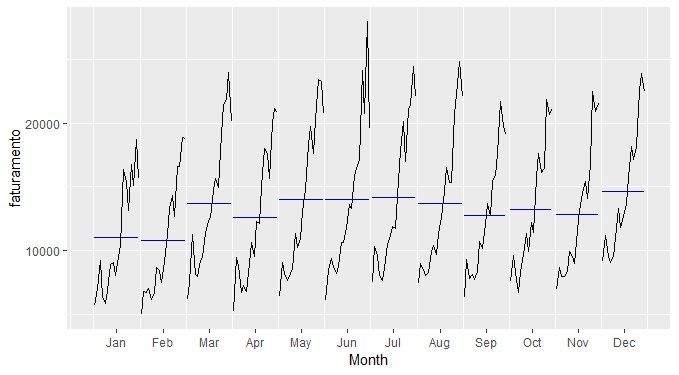
A seguir, plotamos a série sem tendência.
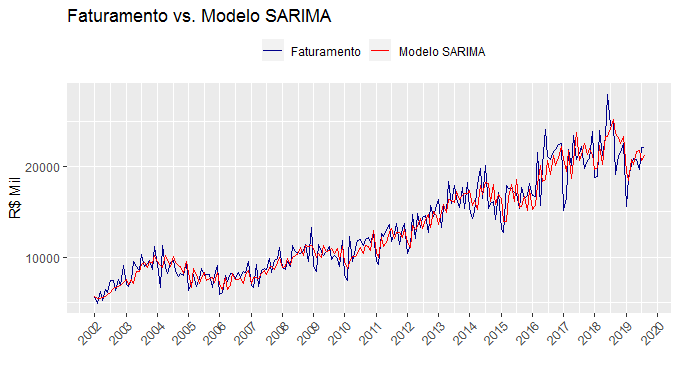
Todos esses aspectos devem ser levados em consideração no momento de construirmos nosso modelo univariado. Uma vez que tenhamos investigado a série, podemos construir nosso modelo SARIMA, plotando o ajuste do modelo como abaixo.
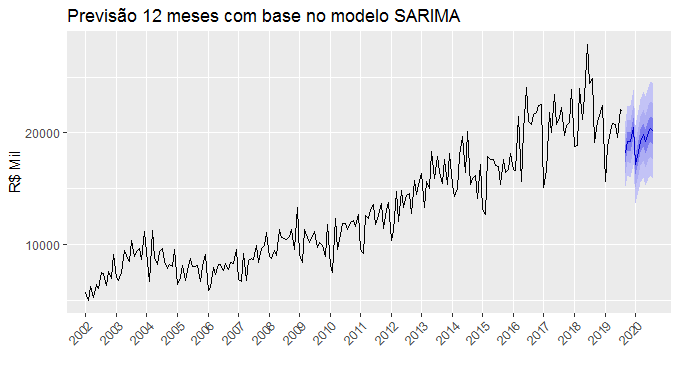
A seguir, plotamos o gráfico com a previsão 12 passos à frente.
A acurácia associada ao modelo é bastante razoável, tratando-se de um modelo univariado. Em outras palavras, a ausência de variáveis preditoras não nos impede de criar um modelo preditivo com acurácia razoável para prever o faturamento de uma determinada empresa. De fato, modelos univariados são bastante utilizados no dia a dia para gerar previsões.
Box, G. E. P.; Jenkins, G. M.; Reinsel, G. C., and Ljung, G. M. Time Series Analysis. Editora Wiley,
2016.
________________________
(*) A metodologia completa está disponível no nosso Curso de Séries Temporais usando o R.
(**) O código completo do exercício estará disponível essa semana no Clube do Código.