No Dicas de R de hoje, seguindo nossa trajetória de modelos de machine learning, vamos introduzir support vector machines (SVMs). Essa metodologia é amplamente utilizada para a classificação de dados que possuem duas classes, porém pode ser expandida para dados com mais classes. Com isso, vamos apresentar a teoria por trás do SVM de modo simplificado, e mostrar como podemos utilizar esse modelo no R.
A ideia por trás do SVM em seu formato mais básico é utilizar a separabilidade das classes para criar um classificador. Para fazer isso, considerando os dados no espaço multi-dimensional das variáveis explicativas, buscamos criar um hiperplano (uma estrutura de menor dimensão que separa o espaço em dois) que prevê a classe de uma observação comparando o valor das variáveis explicativas (ou seja, a posição da observação no espaço) em relação a si. Como de modo geral é possível criar infinitos tais planos, o método básico (chamado de maximal margin classifier) encontra o plano que é mais distante das observações de treino. Com isso, podemos mostrar que esse método depende apenas dos pontos de cada classe que ficam mais próximos do hiperplano, que são chamados de support vectors.
Como apenas esses "pivôs" importam, a variância do método básico é bem alta. Com isso, para reduzir tal variância (e, por consequência, gerando algum viés), podemos permitir que algumas observações de treino fiquem a pouca distância do classificador, ou até mesmo fiquem no lado errado do hiperplano. Esse novo modelo é chamado de support vector classifier, e tem derivação parecida com o anterior, porém compartilha um problema com o primeiro: a dependência da separabilidade.
Pode ser o caso de que a separação entre as classes seja como uma parábola, ou, uma classe fique ao redor da outra no espaço. Nessas situações, um separador linear terá péssimos resultados, exigindo uma maior complexidade da especificação, onde entram então as SVMs. Não vamos entrar em toda a matemática por trás, mas de modo resumido, modelos SVM expandem o universo das variáveis explicativas para suas transformações, criando um hiperplano em volta não apenas das combinações lineares das variáveis em nível como também de funções delas.
Agora, vamos mostrar um exemplo no R de uma SVM. Para isso, utilizaremos o pacote e1071, que implementa diversas ferramentas estatísticas.
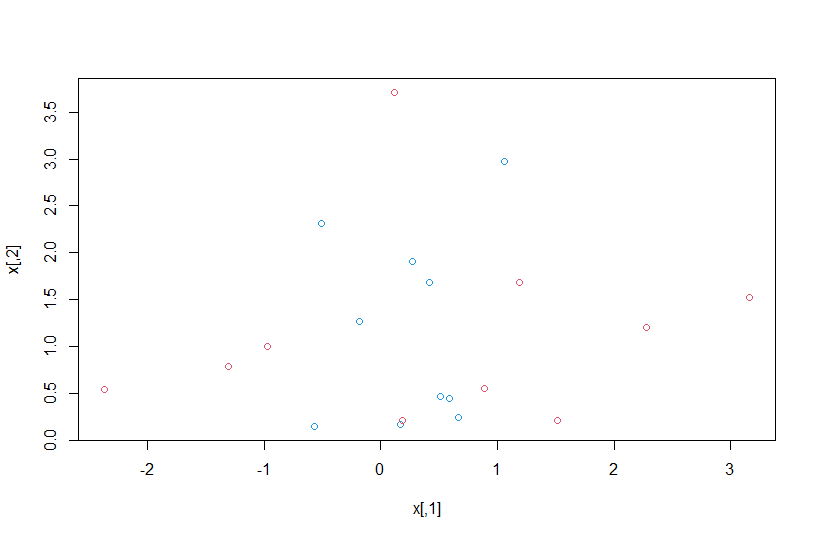
library(e1071) x=matrix(rnorm(20*2), ncol = 2) y=c(rep(-1,10), rep(1, 10)) x[y==1,] = x[y==1,] + 1 plot(x, col=(3-y))
Como podemos ver, os dados gerados não possuem a propriedade de separabilidade, logo o modelo simples não geraria um bom resultado. Abaixo, rodamos o modelo com um separador linear:
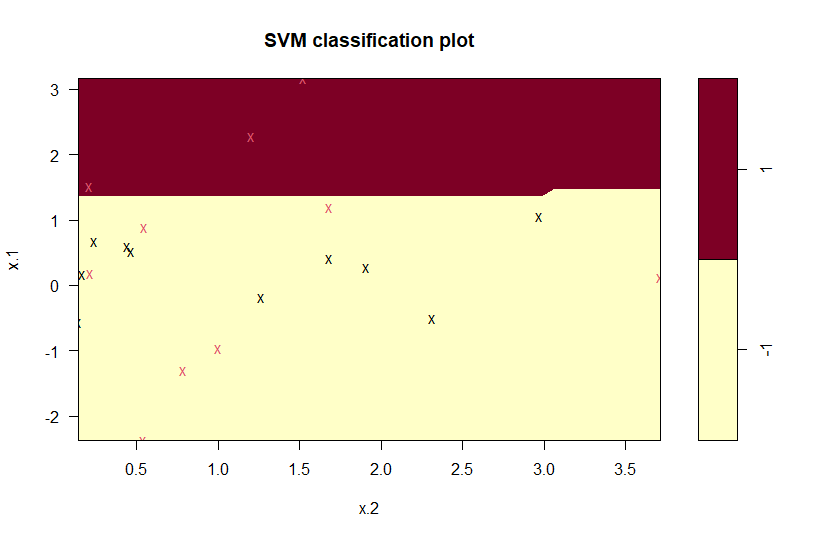
dat=data.frame(x=x, y=as.factor(y)) svmfit=svm(y ~ . , data=dat, kernel= "linear", cost=10, scale=FALSE) plot(svmfit, dat)
Para utilizarmos especificações diferentes, como polinomial e radial, basta modificar o argumento kernel, que define a "máquina" utilizada.
Conteúdos como esse podem ser encontrados no nosso Curso de Machine Learning usando o R.
_____________________