Trabalhos aplicado em economia regional e urbana dependem muito de dados com referência a locais medidos como pontos em espaço, o que gera consequências importantes na análise estatística. Isso acontece pois há dependência espacial entre as observações e pois há heterogeneidade nas relações que estamos modelando. Modelos que levam em conta esses fatores entram no campo de estatística/econometria espacial.
Nessa área é muito comum a utilização de softwares especializados, como o GeoDa. Entretanto, vamos mostrar que é possível realizar esse tipo de operação no R. No post de hoje iremos apresentar como fazer a estimação do Índice de Moran, que permite fazer a clusterização de observações no espaço. Na semana que vem mostraremos como estimar modelos de econometria espacial. Para isso, utilizaremos o pacote spdep.
library(tidyverse) library(geobr) library(sidrar) library(spdep)
Para esse exemplo, iremos usar dados de PIB por microrregião, obtidos pelo pacote sidrar. Veja que estamos centralizando a variável em 0. Então, utilizamos o pacote geobr para fazer o download do mapa e o unimos com os dados.
#Dados de PIB
pib = get_sidra(5938,
variable = 37,
geo = "MicroRegion")</pre>
#Dados de população
pop= get_sidra(202,
variable = 93,
geo = "MicroRegion") %>%
filter(`Sexo (Código)` == 0 & `Situação do domicílio (Código)` == 0)
#Juntando e criando a variável de pib per capita
df <- left_join(pib, pop, by = "Microrregião Geográfica (Código)") %>%
mutate(pibpc = (Valor.x/Valor.y) - mean(Valor.x/Valor.y)) #centralizar no 0
#
mapa_micro = read_micro_region()
mapa_micro$code_micro = as.character(mapa_micro$code_micro)
merged = dplyr::left_join(mapa_micro, df, by = c("code_micro" = "Microrregião Geográfica (Código)"))
Para estimar os modelos da área de econometria espacial é preciso construir a chamada matriz de vizinhança. Essa matriz tem dimensão n x X, sendo n o número de unidades geográficas. No caso deste exemplo, ela mostra quais microrregiões tem vizinhança com quais. Assim, para aquelas em que há vizinhança, há um valor 1. Para todas as outras, 0.
Em sequência é preciso transforma-la em uma matriz de pesos. Uma microrregião com mais vizinhos tem menor peso para cada um deles. Já uma unidade geográfica que tenha apenas 1 vizinho terá peso 1 para este. Assim, utilizamos essa matriz de peso para estimar o chamado I de Moran, que indica o grau de associação espacial da variável que estamos analisando.
nb <- poly2nb(merged, queen=TRUE)
lw <- nb2listw(nb, style="W", zero.policy=TRUE)
moran <- localmoran(merged$pibpc, lw)
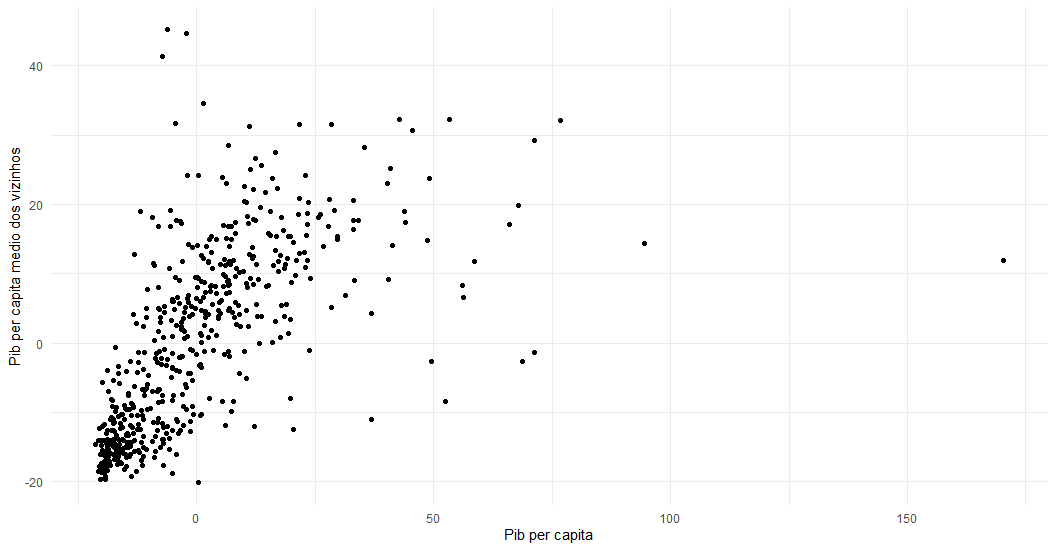
ggplot(merged) +
geom_point(aes(x = pibpc, y =lag_pibpc)) +
theme_minimal() +
xlab("Pib per capita") +
ylab("Pib per capita medio dos vizinhos")
Com isso, separamos as observações com relação estatística significante em quatro grupos a depender se elas estão acima ou abaixo da média de renda e se seus vizinhos estão a baixo e acima da média.
merged$moransig <- moran[,5] #p valor merged$lag_pibpc<- lag.listw(lw, merged$pibpc)</pre> merged <- merged %>% mutate(quadrante = case_when(pibpc >= 0 & lag_pibpc >= 0 & moransig < 0.05~"Alto-Alto", pibpc <= 0 & lag_pibpc <= 0 & moransig < 0.05~"Baixo-Baixo", pibpc >= 0 & lag_pibpc <= 0 & moransig < 0.05~"Alto-Baixo", pibpc <= 0 & lag_pibpc >= 0 & moransig < 0.05~"Baixo-Alto")) <pre>
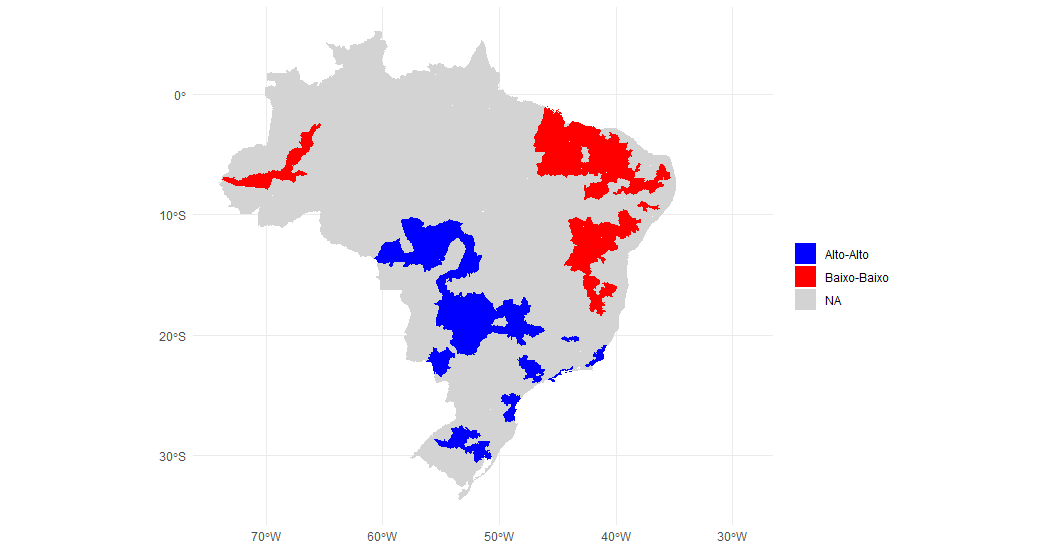
Assim, podemos plotar o mapa dos clusters que estimamos. Veja que apenas dois tipos de clusters estão representados. Isso significa que não há microrregiões ricas com vizinhos pobres ou pobres com vizinhos ricos.
ggplot(merged) +
geom_sf(aes(fill = quadrante), color=NA) +
scale_fill_manual(values = c("blue", "red"), na.value = "lightgrey") +
theme_minimal()