No Hackeando o R de hoje, vamos continuar a desenvolver o ferramental de estatística bayesiana, e para isso vamos mostrar como utilizar a interface do R para o programa JAGS (Just Another Gibbs Sampler), que é especializado em métodos de MCMC. No post da semana passada, apresentamos o algoritmo de Metropolis, que define um passo-a-passo para criar novas observações da distribuição desconhecida dos parâmetros que queremos estimar. Existem outros métodos de gerar essa amostragem, porém não iremos nos preocupar a fundo com eles, e deixar que o JAGS escolha o mais apropriado. Com isso, nosso trabalho passa a ser ter em mãos a distribuição a priori dos parâmetros, e a distribuição dos dados condicionada aos parâmetros. Para reproduzir os códigos desse post, você precisará baixar o JAGS, disponível aqui.
Conforme vimos, para fazer a estimação do parâmetro de interesse, precisamos de uma distribuição a priori, a distribuição condicional de uma amostra, e uma amostra que irá atualizar nossas crenças sobre o parâmetro. A estimação do MCMC será feita pelo JAGS, através do pacote rjags. Esse sistema trabalha com listas, logo devemos gerar uma lista da nossa amostra a partir dos dados dela. Os dados estão disponíveis aqui.
dados <- readr::read_csv('z15N50.csv')
dataList = list(y=dados$y)
Note que geramos uma lista com um único elemento, que é nossa amostra. O próximo passo é definir o modelo, na sintaxe do JAGS. Isso é feito com uma string, que é salva em um arquivo na mesma pasta em que estamos trabalhando. A sintaxe é de modo geral a mesma para os modelos, definindo para cada elemento da amostra (dentro do for) a sua distribuição em função do parâmetro, e a distribuição a priori do parâmetro. Abaixo, definimos uma priori Beta(1, 1), ou seja, uma distribuição uniforme.
modelString = "
model {
for ( i in 1:50 ) {
y[i] ~ dbern( theta )
}
theta ~ dbeta(1,1)
}
"
writeLines( modelString , con="TEMPmodel.txt" )
O último passo que resta para rodarmos o algoritmo é definirmos o ponto inicial. Isso é arbitrário, porém se escolhermos pontos iniciais ruins, a convergência pode demorar, de modo que é preferível que o ponto inicial esteja em uma região de alta probabilidade da posterior. Um método possível é selecionar diversos pontos e rodar múltiplos MCMCs, porém para reduzir o código, vamos utilizar a estimativa de MLE da amostra, que é a média. Novamente, precisamos colocar o elemento em uma lista, e o nome dele deve ser igual ao nome passado ao modelo acima.
thetaInit = sum(dados$y)/length(dados$y) initsList = list(theta=thetaInit)
Com isso, basta carregar o pacote rjags e rodar a função jags.model. Antes de gerarmos nossa cadeia de Markov, tomamos duas medidas iniciais: a adaptação e o burn-in. A adaptação é uma série de amostras que o JAGS extrai para calibrar suas estimativas das condicionais, e também escolher a magnitude ótima para as tentativas de salto que são feitas a cada passo do algoritmo. Esse processo não gera uma cadeia de Markov, logo é descartado do resultado final.
Se nossa estimativa inicial é mal colocada, é possível que ela dê foco demasiado para regiões de baixa probabilidade da posterior nas primeiras observações, até que ela encontre regiões de maior probabilidade. Para evitar que isso contamine a distribuição estimada final, é padrão eliminarmos o trecho inicial do caminho percorrido, chamado de burn-in. Abaixo, deixamos 500 amostras para a adaptação, e 500 amostras de burn-in. Após isso, geramos 3334 da cadeia final com a função coda.samples(), resultando em cerca de 10000 observações, dado que estamos criando 3 cadeias.
library(rjags)
jagsModel = jags.model( file="TEMPmodel.txt" , data=dataList , inits=initsList ,
n.chains=3 , n.adapt=500 )
update( jagsModel , n.iter=500 )
codaSamples = coda.samples( jagsModel , variable.names=c("theta") ,
n.iter=3334 )
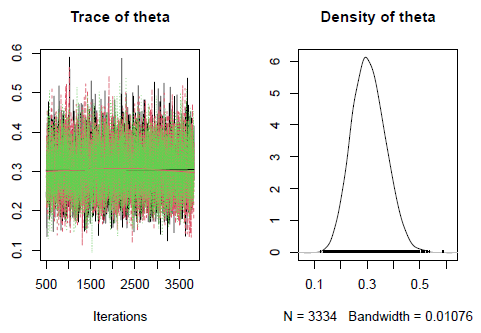
Para visualizar o resultado final, vamos utilizar as visualizações do coda, pacote que gerou as amostras do MCMC. O gráfico da esquerda mostra o caminho de cada simulação, enquanto o da direita é uma combinação das distribuições estimadas de cada cadeia.
plot(codaSamples)
________________________
(*) Para entender mais sobre Estatística Bayesiana, confira nosso Curso de Estatística Bayesiana usando o R.