No Hackeando o R de hoje, vamos finalizar a série sobre estatística bayesiana mostrando como pode ser feita a estimação de um modelo linear simples com MCMC. Diferentemente do método padrão, onde consideramos que a variável de resposta tem distribuição normal após controlarmos para efeitos lineares, os métodos bayesianos permitem maior liberdade quanto às hipóteses tomadas, dado que essencialmente tornam a estimação de parâmetros um problema de seleção de crenças iniciais. No caso a seguir, iremos fazer uma regressão linear robusta, supondo que a distribuição é na verdade uma t de Student.
A distribuição t em sua forma generalizada possui três parâmetros, de média, escala e seus graus de liberdade. Destes, a média é o de maior interesse, pois deve corresponder à previsão do modelo, que, conforme conhecemos, possui dois parâmetros (constante e linear). Note que, com isso, a estimação de y depende de um parâmetro que depende de outros dois, o que torna esse um modelo hierarquizado. Para rodarmos o algoritmo de MCMC, geramos crenças a priori dos parâmetros 'de ponta', e construímos a condicional em passos. Abaixo, geramos o modelo com distribuições usuais:
modelString = "
data {
Ntotal = length(y)
xm = mean(x)
ym = mean(y)
xsd = sd(x)
ysd = sd(y)
for ( i in 1:length(y) ) {
zx[i] = ( x[i] - xm ) / xsd
zy[i] = ( y[i] - ym ) / ysd
}
}
model {
for ( i in 1:Ntotal ) {
zy[i] ~ dt( zbeta0 + zbeta1 * zx[i] , 1/zsigma^2 , nu )
}
zbeta0 ~ dnorm( 0 , 1/(10)^2 )
zbeta1 ~ dnorm( 0 , 1/(10)^2 )
zsigma ~ dunif( 1.0E-3 , 1.0E+3 )
nu ~ dexp(1/30.0)
beta1 = zbeta1 * ysd / xsd
beta0 = zbeta0 * ysd + ym - zbeta1 * xm * ysd / xsd
sigma = zsigma * ysd
}
"
writeLines( modelString , con="TEMPmodel.txt" )
É importante notar que fizemos a padronização dos dados para rodar o modelo. Isso não é necessário, porém facilita a convergência do MCMC. Após isso, basta carregar os dados, disponíveis aqui,
e rodar o modelo.
myData = read.csv(file="HtWtData30.csv" )
xName = "height" ; yName = "weight"
y = myData[,yName]
x = myData[,xName]
dataList = list(
x = x ,
y = y
)
library(rjags)
parameters = c("beta0", "beta1", "sigma", "nu" )
jagsModel = jags.model( "TEMPmodel.txt" , data=dataList ,
n.chains=4 , n.adapt=500)
codaSamples = coda.samples(jagsModel, variable.names = parameters,
n.iter= 50000, thin=1)
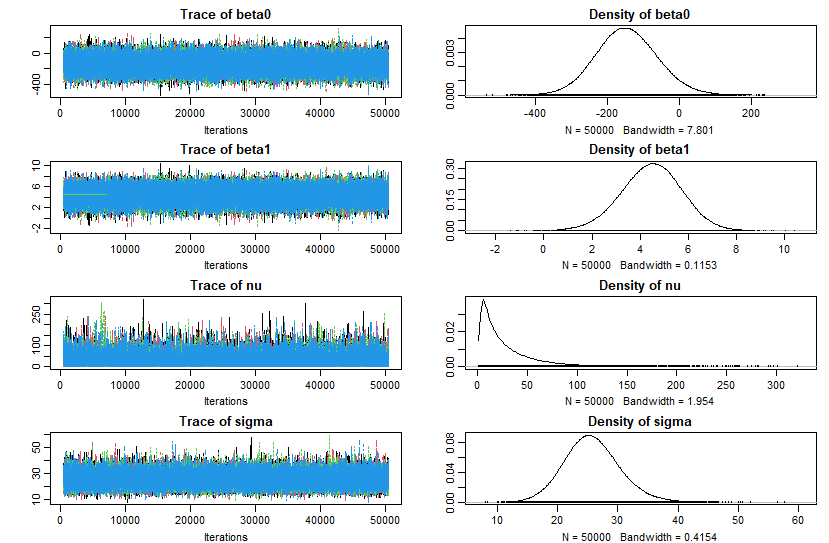
plot(codaSamples)
___________
(*) Gostou? Conheça nosso Curso de Estatística Bayesiana usando o R.