A gestão de portfólio tem como seu máximo expoente Harry Markowitz, pioneiro da seleção da carteira e da teoria que leva o seu próprio nome: Teoria de Markowitz. A teoria teve um impacto enorme no mundo das finanças, cumprindo o objetivo de minimizar o risco de uma carteira de investimento e rendendo ao autor até mesmo um prêmio Nobel. No post de hoje, iremos dar uma olhada na teoria da seleção de carteira e na teoria de Markowitz.
A gestão de portfolio tem como principal objetivo lidar com a gestão de risco de um número de ativos financeiros em um conjunto em que todos os ativos estão contidos na mesma carteira de investimentos. Mas afinal, qual o beneficio da escolha de vários ativos financeiros em uma carteira? A questão é que, por suposição, quanto maior o número de ativos em uma carteira, menos risco o investidor incorrerá, mas como isso é possível?
Dado o contexto de que o Retorno de um ativo é dado por:
![\[R_t = ln(\frac{P_t}{P_t-1})\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-32b533483cd6d3c9c26adf4e9f49fd2c_l3.png "Rendered by QuickLaTeX.com")
Ou seja, o log-retorno 
é dado pelo logaritmo natural do preço de hoje divido pelo preço de ontem.
O retorno de um ativo é a estrutura do estudo, pois é basicamente dele que é encontrado duas importantes medidas de estimação para que possamos realizar o cálculo do risco do nosso conjunto de ativos e encontrar os pesos ideais de um portfólio, essas duas medidas são a média e a variância (mean-variance).
A média dos retornos, a grosso modo, seria o Retorno Esperado no nosso investimento, baseado na média amostral dos retornos históricos do nossos ativos.
![\[E(R) = \frac{\sum_{t = 1}^{T}(R_it)}{T}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-3e261764e29d39150481b522178567af_l3.png "Rendered by QuickLaTeX.com")
Por outro lado, a variância, ou o que em finanças é chamado de volatidade ou risco, também mensurado pelo desvio padrão, que é dado por:
![\[\sigma^2 = \frac{(E[(R_i - \mu)^2])}{T-1}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-00b29c6df0f4d1c34d73d2d0d93b6009_l3.png "Rendered by QuickLaTeX.com")
Dito isso, sabemos que estamos lidando com ativos individuais, porém, como o contexto é dado pelo retorno de um conjunto de ativos, devemos calcular os estimadores corretos, buscando encontrar o retorno e a variância do portfólio.
O Retorno de um portfólio é calculado como:
![\[R_p = \sum_{i=1}^n(W_iR_i)\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d56f291196afc510c8dbbd4984626249_l3.png "Rendered by QuickLaTeX.com")
Ou seja, o retorno do ativo 
ponderado pelo seu peso 
.
Para o seu retorno esperado, calcula-se como a média amostral de seus retornos passados, assim como o retorno esperado de um único ativo
Por outro lado, a variância de um portfólio não é igual ao calculo da variância de um ativo individual. Quando estamos falando em risco de um ativo, sabe-se que eles podem incorrer dos mesmo riscos. Seja dois ativos que possuem risco cambial ou risco de mercado, tem-se que levar em conta essas duas questões ao realizar o calculo do risco de um portfólio.
Portanto, para computar esses tipos de riscos, podemos fazer isso através de duas importantes medidas estatística: covariância e correlação
A covariância permite que seja calculado a dependência linear entre as variáveis. O mesmo serve para a correlação, que diferente da covariância, é uma medida em forma percentual. Quando medimos a covariância (ou correlação) de dois ou mais ativos, estamos considerando o quanto os ativos se movimentam em relação ao outro, se positivamente ou negativamente.
Calculamos a covariância como:
![\[\sigma_{jk}=\frac{\sum_{t=1}^T[R_{jt}-\bar{R}_j][R_{kt}-\bar{R}_k]}{T-1}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-384b9130fa59eb60606e9f881ee7d281_l3.png "Rendered by QuickLaTeX.com")
Quando ocorre de os ativos terem covariância negativa, a variância ou risco do portfólio tende a diminuir. Quando a covariância é positiva, o risco do portfólio tende a aumentar. Essa questão é um principio básico da diversificação. Quanto menor a covariância dos ativos em uma carteira, menor o risco, quanto maior a covariância, maior o risco.
Sendo assim, calcula-se o risco (variância) de um portfólio como:
![\[\sigma_P=\sqrt{\sum_{j=1}^N(w_j^2 \sigma_j^2)+\sum_{j=1}^N\sum_{\substack {k=1 \\ k \neq j}}^N(w_j w_k \sigma_{jk})}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-cbe042737fbab09dffa4d1bd7ce6f104_l3.png "Rendered by QuickLaTeX.com")
Mas todo o papel da covariância e variância dos ativos individuais em uma carteira, dependerá de seus pesos. Isto leva a crer que pode existir um combinação grande de pesos para uma só carteira, e o investidor se vê tentado a tentar uma combinação que melhor satisfaça suas preferências. Em muitos casos, a preferência que melhor pode atender a todos será a combinação de pesos de ativos que melhor minimize o risco do portfólio.
Para isso, Markowitz criou um método para que seja possível descobrir o pesos tal qual a relação de risco x retorno melhor se satisfaz dentro de um contexto que o retorno esperado é dado pela média amostral dos retornos e o risco é dado pela variância e covariância dos ativos.
O ponto em que é conhecido como aquele em que é minimizado o risco dados os estimadores, é conhecido como portfólio de variância mínima. Esse ponto é resolvido a partir de um problema de otimização, que possui algumas restrições; 1) a soma das proporções alocadas em cada ativo tem que ser igual a um; 2) cada ativo tem que ter peso maior ou igual a zero; 3) em cada problema escolhemos um retorno esperado para o qual minimizaremos o risco.
A otimização é dado por:
![\[min_{w_i} \sum_{j=1}^N(w_j^2 \sigma_j^2)+\sum_{j=1}^N\sum_{\substack{k=1 \\ k \neq j}}^N(w_j w_k \sigma_{jk})\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-b901f1f6cfc35a685c9c6e7bf07d272c_l3.png "Rendered by QuickLaTeX.com")
s.a.
Como dito, a solução deste problema nos dá os pesos ótimos para investir em cada um dos ativos.
A partir da teoria, podemos calcular o ponto mínimo de um portfólio dentro do R. Para isso, utilizamos o pacote {PortfolioAnalytics}, que permite configurar um portfólio e calcular a partir de restrições escolhidas.
Primeiro, devemos coletar os dados dos ativos.
library(quantmod) library(PerformanceAnalytics) library(PortfolioAnalytics) library(tidyverse)
Como obrigatório, devemos ter em mãos os retorno dos nossos ativos.
# Define os ativos que irão ser coletados
tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")
# Define a data de início da coleta
start <- as.Date("2016-12-01")
# Realiza a coleta dos preços diários
prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Cl(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)
# Transfroma os preços diários em mensais
prices_monthly <- to.monthly(prices,
indexAt = "lastof",
OHLC = FALSE)
# Calcula os retornos mensais
asset_returns <- Return.calculate(prices_monthly,
method = "log") %>%
na.omit()
Com os retornos em mãos, configuramos as restrições e os objetivos do nosso portfólio.
# Define os nomes dos ativos na especificação portfolio_spec <- portfolio.spec(assets = tickers) # Considera que a soma dos pesos será igual a 1 portfolio_spec <- add.constraint(portfolio = portfolio_spec, type = "full_investment") # Não permite vendas a descoberto portfolio_spec <- add.constraint(portfolio = portfolio_spec, type = "long_only") # Adiciona os objetivos - Retorno esperado através da média amostral portfolio_spec <- add.objective(portfolio = portfolio_spec, type = "return", name = "mean") # Adiciona os objetivos - Risco esperado através do desvio padrão portfolio_spec <- add.objective(portfolio = portfolio_spec, type = "risk", name = "StdDev")
Por fim calculamos o portfolio através da otimização pelo método "random" no qual o solver irá ser uma combinação de diferentes pesos do portfólio.
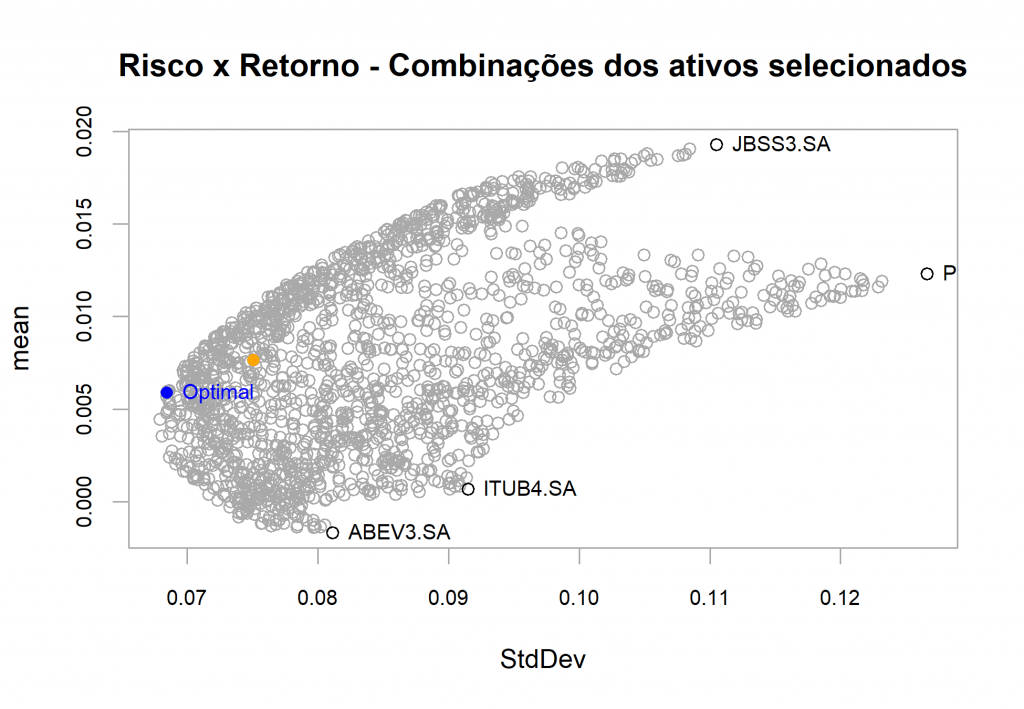
# Calcula a otimização do portfólio opt <- optimize.portfolio(asset_returns, portfolio = portfolio_spec, optimize_method = "random", trace = TRUE) # Plota o gráfico de Risco x Retorno chart.RiskReward(opt, risk.col = "StdDev", return.col = "mean", chart.assets = TRUE, main = "Risco x Retorno - Combinações dos ativos selecionados")
Vemos no gráfico os resultados de retorno e risco para as diferentes combinações de pesos dos ativos no portfólio. O ponto azul, é o ponto que minimiza os risco de acordo com a equação de Markowitz.
________________________
(*) Para entender mais sobre Mercado Financeiro, seleção de carteira e a Teoria de Markowitz, confira nosso curso de R para o Mercado Financeiro.
________________________
