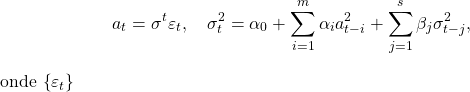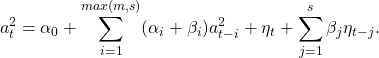Volatilidade e modelos ARCH e GARCH

A volatilidade é uma forma de avaliação para ativos e séries financeiras mais importante do mundo das finanças. Esse indicador permite que seja avaliado o risco de um ativo, e com base na sua análise se tome a melhor decisão possível na alocação dos investimentos. Entretanto, a volatilidade possui diversas características que devem ser avaliadas de forma detalhada, não somente de forma descritiva, mas também para a construção de modelos. No post de hoje, iremos introduzir as características da volatilidade de séries financeiras e os modelo ARCH e GARCH.

Volatilidade

Modelos econométricos (os mais conhecidos) de séries univariadas, visam estimar o retorno esperado de uma série financeira, se preocupando apenas com o primeiro momento condicional da série. Na vida real, esse fato pode não ocorrer, afinal, ao estar consciente da queda passada de um ativo, ocorre um viés no investidor, o fazendo criar uma expectativa negativa futura sobre o ativo, afetando os seus valores futuros.

Outro ponto importante é que a volatilidade é não observável diretamente, ou seja, é necessário obter uma forma de estimá-la através de seus preços. Mas, mesmo que tenhamos isso em mente, devemos conhecer mais algumas caraterísticas importantes sobre a volatilidade para não incorrermos em erros nas avaliações e na montagem de modelos.

A volatilidade é alta em certos períodos e baixa em outros, configurando o que a literatura
chama de volatility cluster;
A volatilidade evolui de maneira contínua, de modo que saltos não são comuns;
A volatilidade costumar variar em um intervalo fixo (isso significa que a volatilidade é estacionária);
A volatilidade costuma reagir de forma diferente a um aumento muito grande nos preços e a um decréscimo igualmente muito grande, com o último representando maior impacto.


library(quantmod)
library(PerformanceAnalytics)
library(magrittr)
library(zoo)
library(fGarch)

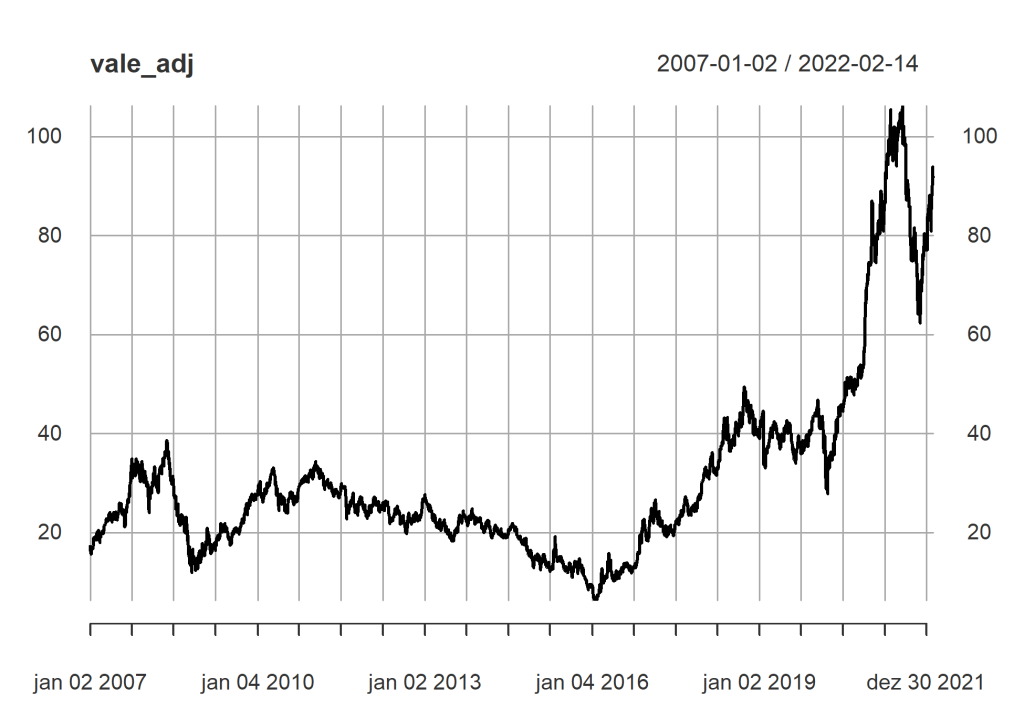
De forma a compreendermos melhor as característica, iremos utilizar a série de preços ajustada da VALE3.

# Busca a série de preços da VALE3
getSymbols("VALE3.SA",
auto.assign = TRUE,
warnings = FALSE,
src = "yahoo")

# Retira o preço ajustado

vale_adj <- Ad(VALE3.SA)

# Gráfico do preço

plot(vale_adj)

Apesar de ser o ponto inicial, as características de um série de preço não é útil o suficiente para trabalharmos com a estimação da volatilidade, para isso, devemos realizar uma transformação para que a nossa série seja estabilizada e transformada em estacionária. A forma mais comum é realizar uma transformação em log, e depois retirar a primeira diferença da série, essa mudança é bem conhecida, sendo chamada de Retorno Contínuo.

Para o Retorno contínuo diário, temos, por suposto, algumas propriedades:

- O retorno médio é zero
- a variação do retorno muda ao longo do tempo
- com base nos retornos contínuos, calculamos uma medida de volatilidade (risco), com base no seu desvio padrão.

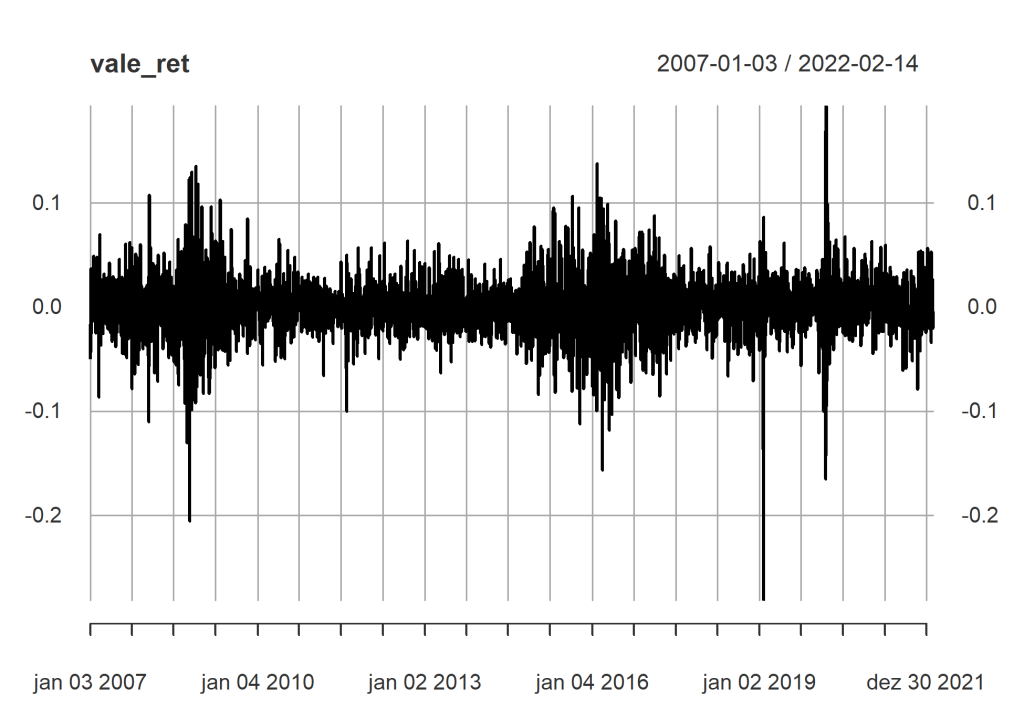
# Calculo os retornos contínuos

vale_ret <- diff(log(vale_adj)) %>%
na.omit()

# Gráfico do retorno contínuo diário

plot(vale_ret)

Vemos através do gráfico dos retornos diários que há períodos em que ocorre uma maior variação em relação a outros períodos.

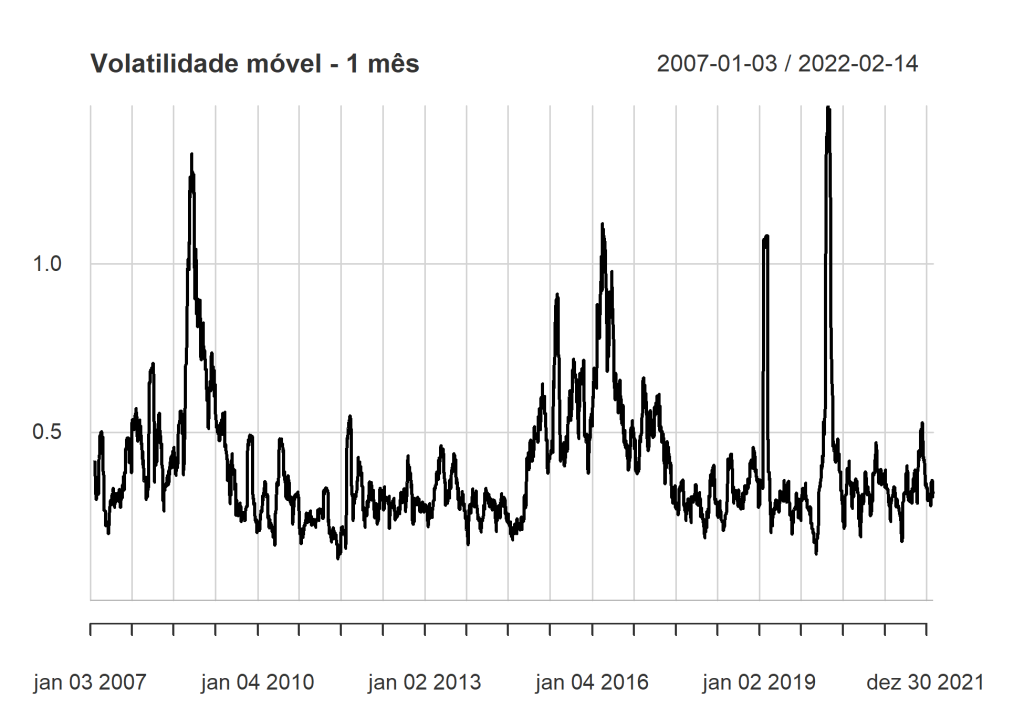
Uma outra forma interessante de acompanhar essa variação ao longo do tempo é construindo um gráfico de volatilidade móvel mensal.

chart.RollingPerformance(R = vale_ret,
width = 22,
FUN = "sd.annualized",
scale = 252,
main = "Volatilidade móvel - 1 mês")

Com base nos gráficos, podemos entender que nossa série possui algumas características da volatilidade.

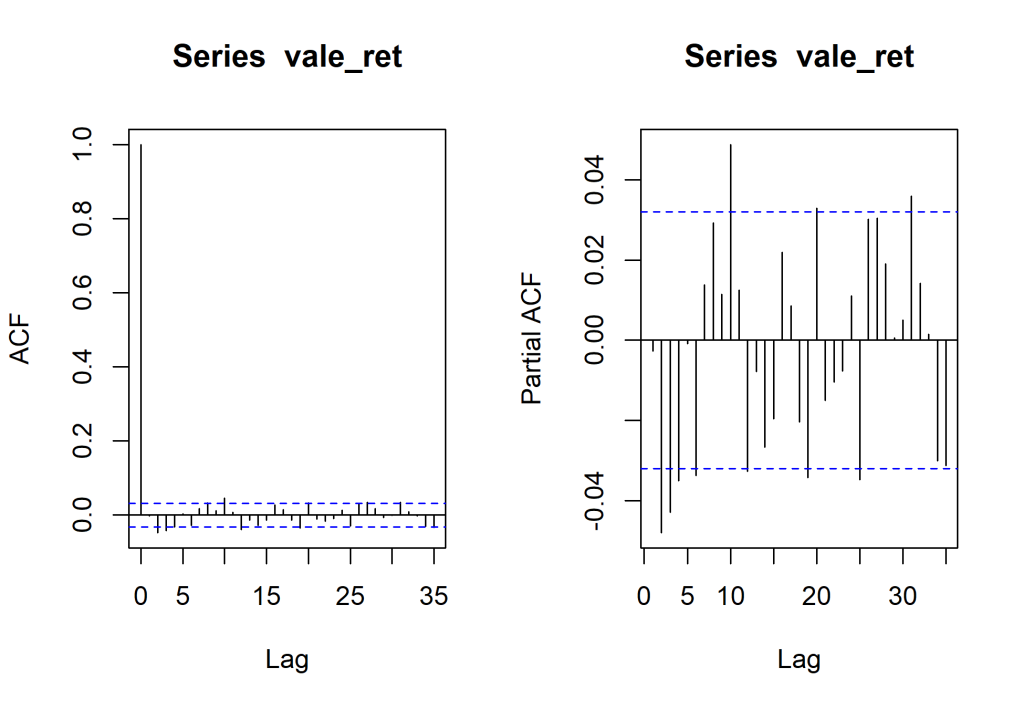
par(mfrow = c(1,2))

# Gráfico de auto correlação

acf_ret <- acf(vale_ret)

# Gráfico de auto correlação parcial

pacf_ret <- pacf(vale_ret)

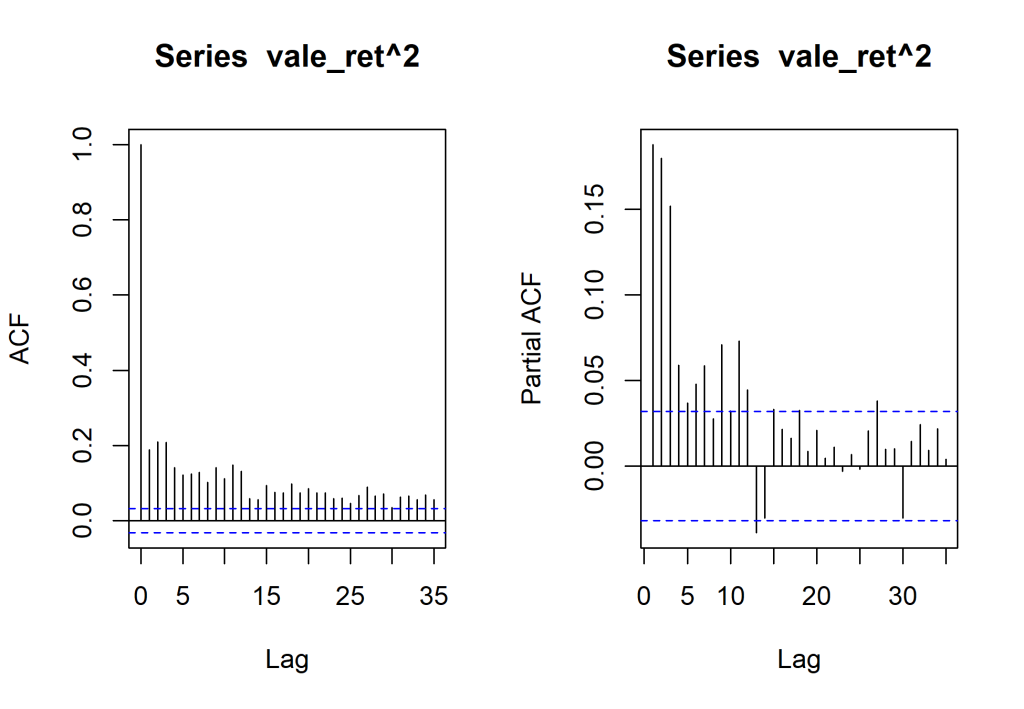
Porém, para que possamos entender melhor a ideia de heterocedasticidade condicional, utilizamos o quadrado da série para que seja possível ver que elas não são independentes e que variancia é correlata.

par(mfrow = c(1,2))

# Gráfico de auto correlação dos retornos ao quadrado

acf_ret_ <- acf(vale_ret^2)

# Gráfico de auto correlação parcial do retornos ao quadrado

pacf_ret_ <- pacf(vale_ret^2)

Vemos a diferença as funções de autocorrelação, para confirmar esse ponto, realizamos um teste para confirmar.

Box.test(coredata(vale_ret^2), lag = 12, type = "Ljung")

Nós podemos rejeitar a hipótese nula de não autocorrelação nos retornos contínuo ao quadrado.

Construção do modelo

Com isso, entendemos que há existência de clusters de volatilidade e que os retornos próximos da série tendem a ter níveis de volatilidade semelhante, sendo assim, é necessário ter isso em mente na construção de modelos.

ARCH

O primeiro modelo que teve essa estrutura em sua base foi o ARCH (Autoregressive Conditional Heteroskedasticity), que pode ser definido na equação

(1) $\begin{align*} a_t = \sigma_t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \alpha_1 \sigma_{t-1}^2 + ... + \alpha_m \sigma_{t-m}^2 \end{align*}$

onde $\varepsilon_t$ é uma sequência de variáveis aleatórias independentes e identicamente distribuídas com média zero e variância igual 1, $\alpha_0 > 0$ e $\alpha_i \geq 0$ para $i > 0$ .

Um modelo ARCH(m) é aquele em que a variância no tempo t é condicional as observações passadas da série m vezes, utilizando o quadrado das observações passadas.

arch1 <- garchFit(~1+garch(1, 0), data = vale_ret, trace = F)

GARCH

Por outro lado, podemos pensar também em considerar não somente as observações passadas, como também as variâncias passadas, adicionando no modelo mais parâmetros. Esse modelo é conhecido como GARCH ( Generelized Autoregressive Conditional Heteroskedasticity), com a equação

(2) $\begin{align*} a_t = \sigma^t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \sum_{i=1}^{m} \alpha_i a_{t-i}^2 + \sum_{j=1}^{s} \beta_j \sigma_{t-j}^2, \end{align*} onde $\left \{ \varepsilon_t \right \}$$

é também uma sequência de variáveis aleatórias iid com média zero e variância igual a 1, $$\alpha_0 > 0$, $\alpha_i \geq 0$, $\beta_j \geq 0$ e $\sum_{i=1}^{max(m,s)} (\alpha_i + \beta_i) < 1$.$ De modo a entender as propriedades do modelo GARCH, convém fazer algumas modificações. Tomemos $\eta_t = a_t^{2} - \sigma_t^{2}$, assim $\sigma_t^{2} = a_t^2 - \eta_t$ . Iterando $\sigma_{t-i}^2 = a_{t-i}^2 - \eta_{t-i}$ para $(i = 0,...,s)$ na equação, nós podemos reescrever o modelo GARCH como

(3) $\begin{align*} a_t^2 = \alpha_0 + \sum_{i=1}^{max(m,s)} (\alpha_i + \beta_i) a_{t-i}^2 + \eta_t + \sum_{j=1}^{s} \beta_j \eta_{t-j}. \end{align*}$

Assim, o modelo GARCH pode ser considerado uma aplicação da ideia dos modelos ARMA ao quadrado de $a_t$ .

garch1 <- garchFit(~1+garch(1,1), data = vale_ret, trace = F)

Oferta Especial!

No próximo dia 17, das 9h às 19h da manhã, você terá a chance de participar do pré-lançamento do treinamento Análise de Dados Macroeconômicos e Financeiros no R. Para concorrer a uma das vagas com desconto, acesse o link e conheça os detalhes.

____________________

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise regional do mercado de trabalho com dados do CAGED usando Python

Como coletar dados do Banco Central Europeu (ECB) usando a API com o Python?

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

Criando Tabelas com o Python: mostrando o poder da linguagem sobre o Excel

Análise do Censo Demográfico com o R

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Outros artigos relacionados

Análise regional do mercado de trabalho com dados do CAGED usando Python

Os microdados dos CAGED fornecem informações detalhadas a nível de cidade, sexo, raça, nível de instrução, idade, salário e outras sobre os trabalhadores formais do Brasil, possibilitando ricas análises regionais de dados. Neste artigo mostramos como acessar, processar e analisar estes dados utilizando o Python.

Como coletar dados do Banco Central Europeu (ECB) usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal do ECB através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.

Transfer Learning: mostrando porque o Python está na ponta do desenvolvimento

A aprendizagem por transferência (transfer learning) é o reuso de um modelo pré-treinado em um novo problema. Portanto, sua utilização torna-se um avanço enorme para a previsão de diferentes tipos de variáveis, principalmente para aquelas ordenadas no tempo. Mostramos nesta postagem o uso do Transfer Learning com o Python para o caso de Séries Temporais.