Um importante conceito do mundo das finanças é o Beta de mercado, no qual mensura a exposição de ações ou portfólios aos movimentos do portfolio de mercado, este sendo representado por índices, tal como o Ibovespa. O método mais comum de avaliar o Beta é através do Capital Asset Pricing Model (CAPM), um modelo de precificação de ativos que a partir da construção do Beta, avalia o retorno esperado de um ativo. No post de hoje introduziremos o conceito de Beta de mercado e o estimaremos através do R e do Python.
O CAPM é um modelo criado na década de 1970, a partir de uma conjunção de estudos protagonizamos pela Teoria Moderna do Portfólio. O CAPM estima o retorno esperado de um ativo com base no retorno de mercado (isto é, o retorno da carteira de mercado, representando aquela carteira que não possui risco idiossincrático ou que somente possui o risco sistemático) e pela Taxa de Juros Livre de risco.
Com o retorno da carteira de mercado representando o risco sistemático, chega-se a conclusão de que as variações do portfólio de mercado representaria um fator importante na variação do retorno de uma ação. Para tanto, na formulação do CAPM foi levado em conta o quanto estes retornos se relacionam, representado pelo Beta de mercado, formando então a seguinte equação calculada através de uma Regressão Linear via MQO:
em que representa o excesso de retorno de um ativo, dado pela subtração do retorno do ativo em relação ao retorno da taxa de juros livre de risco.
o excesso de retorno do portfolio de mercado, sendo representado pela diferença do retorno de mercado e do retorno da taxa de juros livre de risco.
é o coeficiente da regressão que demonstrará o efeito da variação do excesso de retorno do mercado no excesso de retorno do ativo.
é o erro da regressão.
O objetivo então é obter as reais taxas de retorno do ativo e do portfólio de mercado e calcular o Beta de mercado (coeficiente de regressão) . Para tanto, podemos utilizar o R e o Python para coletar os dados e obter o cálculo do Beta de mercado.
A importação dos dados será feita por meio do NEFIN e do Yahoo Finance. Na primeira fonte buscaremos os dados da taxa de juros livre de risco, calculado por meio do DI Swap de 30 dias e o excesso de retorno do mercado, calculado por meio de um portfólio de ações criado a partir de critérios definidos pelo NEFIN e pela diferença com a taxas de juros livre de risco.
Beta no R
O primeiro passo será buscar as séries no site do NEFIN. Utilizaremos a planilha disponibilizada pelo site e devemos realizar algumas manipulações e limpeza para poder utiliza-la.
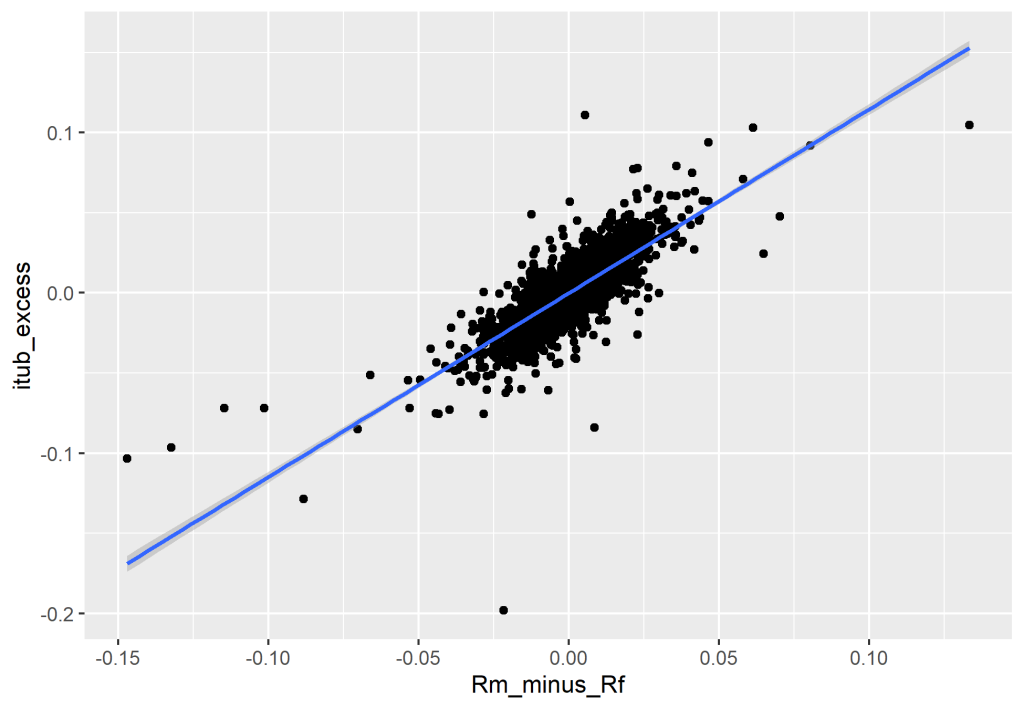
Com o excesso de retorno da carteira de mercado e a taxa de juros livre de risco em mãos, buscaremos o preço de uma ação como exemplo. Aqui utilizaremos a ação ITUB4, no qual iremos importar através da função tq_get() do pacote {tidyquant}. Transformamos os preços da ação em log de retornos com a função tq_transmute() como um wrapper da função dailyReturn().
Por fim, rodamos a regressão através da função lm() e obteremos o Beta de Mercado através do Coeficiente Estimado no valor de 1.1472.
 Beta no Python
Beta no Python
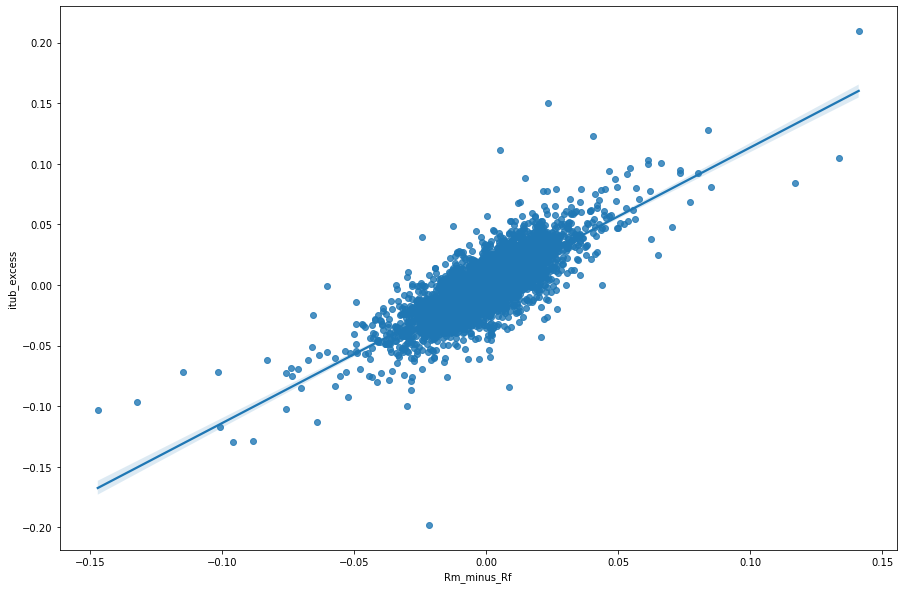
No Python seguiremos o mesmo processo que realizamos no R. Primeiro capturamos os dados do NEFIN, em seguida buscamos o preço de fechamento da ITUB4 e transformamos em log retornos, e por fim calculamos o Beta através de uma regressão.