A taxa de juros de um país define grande parte das decisões de curto e longo prazo dos agentes econômicos. No post de hoje, iremos analisar a relação entre a Taxa de Juro Real do EUA e o Índice S&P 500.
Ao lembrarmos do cálculo de preço de uma ação de uma empresa, consideramos que o seu preço hoje é definido com base nos fluxos de caixa esperados para a companhia ao longo do tempo, trazidos a valor presente por uma taxa de desconto. Essa taxa de desconto é afetada, em partes, pela taxa de juro real da economia.
A taxa de juro real (ex-ante) é calculada de acordo com o juro nominal e a expectativa de inflação de um país. Em termos exatos, é definido pela equação:
Essa equação é usualmente aproximada pela taxa de juros menos a taxa de inflação:
r ≅ i – π
Essa aproximação é útil para taxa relativamente pequenas da taxa de juros e de inflação.
Voltando para o efeito da taxa de juro real em relação as empresas, é fácil perceber que não somente o juros nominais afetam severamente as decisões de curto prazo de agente, mas também as de longo prazo. Além disso, é importante reconhecer que há a necessidade de realizar o ajuste do juros pela expectativas na inflação. A suposição, é que quanto mais elevado a taxa de juro real de uma economia, mais descontado será o preço de empresas em uma bolsa, portanto, haverá relações negativas entre as duas variáveis.
Para avaliar essa suposição, e consequentemente o relacionamento entre o efeito taxa de juros reais sobre as empresas, usaremos o índice S&P 500 e a taxa de juros reais de 10 anos do EUA.
Coleta e análise os dados da Taxa de Juros Real do EUA
A Taxa de Juro Real do EUA é obtida através do FRED, especificadamente pelo código REAINTRATREARAT10Y, referente a Taxa de Juro de 10 anos, em frequência mensal. A instituição também disponibiliza as Taxas em 1 mês e 1 ano, também com frequência mensal.
Coletamos os dados por meio da função getSymbols, do pacote {quantmod}, utilizando o código e relatando a fonte dentro da função.
library(timetk) library(feasts) library(tsibble) library(ggplot2) library(patchwork) library(dplyr) library(quantmod) library(forecast)
### Coleta de dados - Juros reais - 10-Year Real Interest Rate
getSymbols('REAINTRATREARAT10Y',
src = 'FRED'
)
### Tratamento - Juros reais - 10-Year Real Interest Rate
real_int <- REAINTRATREARAT10Y |>
tk_tbl(preserve_index = TRUE,
rename_index = 'date') |>
rename(real_int = REAINTRATREARAT10Y) |>
mutate(date = yearmonth(date)) |>
as_tsibble(index = date)
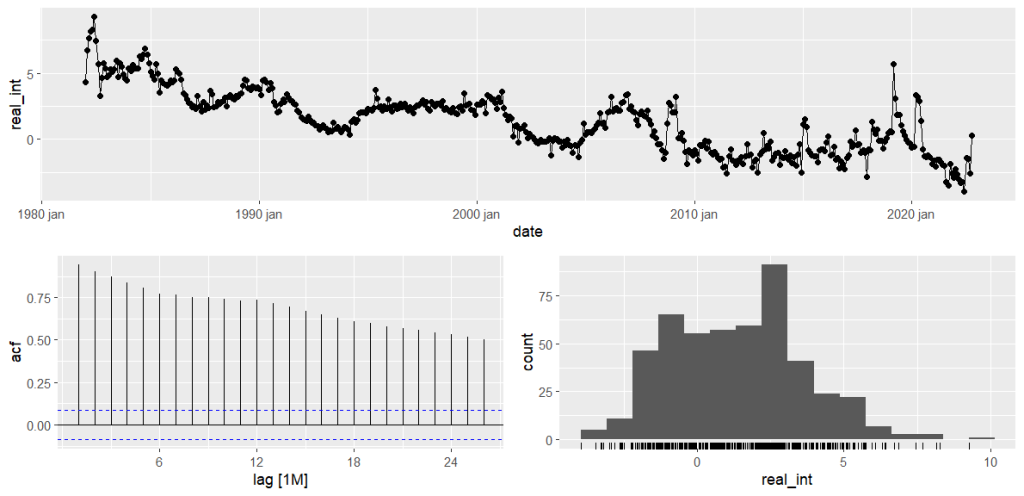
Para o tratamento, transformamos os dados em tibble, e posteriormente em tsibble. Isso permitirá o uso de funções gráficas do pacote {feast}. Vejamos abaixo os gráficos da Taxa de Juros Real - 10 anos, vemos que há uma tendência de queda do indicador, bem como pequenos pontos de volatilidades ao longo do tempo.
</pre>
### Analisando - Juros reais - 10-Year Real Interest Rate
real_int |>
gg_tsdisplay(y = real_int,
plot = c("histogram"))
 Coleta e análise os dados do S&P 500
Coleta e análise os dados do S&P 500
O Standard & Poor's 500 é um índice composto por cerca de 500 ativos. Vamos utiliza-lo como medida que represente as empresas norte americanas. Abaixo, coletamos os dados do índice através do Yahoo Finance, por meio do pacote {quantmod}, utilizando a função getSymbols.
</pre>
### Coleta de dados - S&P 500
getSymbols('^GSPC',
src = 'yahoo',
from = min(index(REAINTRATREARAT10Y))
)
### Tratamento de dados - S&P 500
sp_monthly_tbl <- to.monthly(GSPC) |>
tk_tbl(preserve_index = TRUE,
rename_index = 'date') |>
select(date,
price_adjusted = GSPC.Adjusted
) |>
mutate(date = yearmonth(date)) |>
as_tsibble(index = date)
<pre>
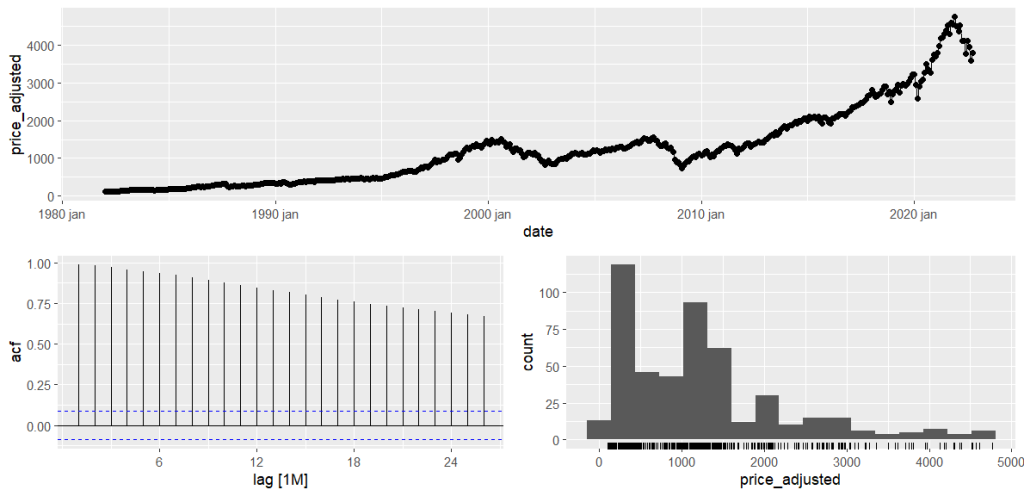
Na parte de tratamento dos dados, alteramos a frequência para mensal (como forma de igualar o período com a Taxa de Juros Real), além de transformar em tibble (os dados são importados em classe xts), e posteriormente em tsibble.
Pelo gráfico, é possível perceber que há uma tendência de alta no índice.
</pre>
### Analisando - S&P 500
sp_monthly_tbl |>
gg_tsdisplay(y = price_adjusted,
c("histogram"))
<pre>
 Qual a relação entre as duas variáveis?
Qual a relação entre as duas variáveis?
Acima entendemos as propriedades estatísticas de ambas as variáveis. Seguiremos a construir uma forma de obter o relacionamento entre ambas as variáveis.
</pre>
### Relação entre as variáveis
ir_plot <- ggplot(real_int, aes(x = date))+
geom_line(aes(y = real_int), size = 0.8, color = "darkblue")+
scale_y_continuous(breaks = seq(-3, 8, by = 2),
labels = scales::label_percent(scale = 01))+
labs(title = "Juros reais - 10-Year Real Interest Rate",
subtitle = "Código: REAINTRATREARAT10Y",
x = '',
y = '',
caption = "Fonte: FRED | Elaborado por: analisemacro.com.br")
sp_plot <- ggplot(sp_monthly_tbl, aes(x = date))+
geom_line(aes(y = price_adjusted), size = 0.8, color = "darkred")+
labs(title = "Índice S&P 500",
subtitle = "Código: ^GSP",
x = '',
y = '',
caption = "Fonte: Yahoo Finance | Elaborado por: analisemacro.com.br")
# Coloca lado a lado com o {patchwork}
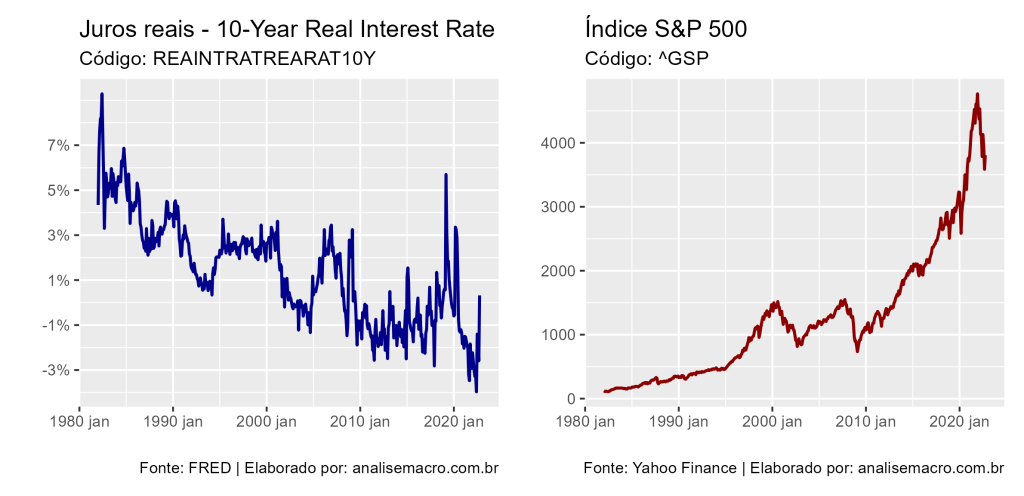
ir_plot + sp_plot
<pre>
É possível analisar os gráficos da séries em conjunto. Vemos que a direção das séries são opostas ao longo do tempo, isso compactua com a suposição criada.
# Junta os dados all_data <- real_int |> inner_join(sp_monthly_tbl, by = 'date') |> mutate(price_adjusted = log(price_adjusted))
</pre> ### Correlação correlation::correlation(all_data) # Parameter1 | Parameter2 | r | 95% CI | t(488) | p # ------------------------------------------------------------------------- # real_int | price_adjusted | -0.78 | [-0.81, -0.74] | -27.32 | < .001*** # # p-value adjustment method: Holm (1979) # Observations: 490 <pre>
</pre> ## Regressão Linear Simples reg_ir_sp <- dynlm::dynlm(price_adjusted ~ real_int, data = all_data) summary(reg_ir_sp) # Time series regression with "numeric" data: # Start = 1, End = 490 # # Call: # dynlm::dynlm(formula = price_adjusted ~ real_int, data = all_data) # # Residuals: # Min 1Q Median 3Q Max # -1.35722 -0.46678 -0.08593 0.46985 2.55749 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 7.18976 0.03080 233.43 <2e-16 *** # real_int -0.31538 0.01154 -27.32 <2e-16 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.5842 on 488 degrees of freedom # Multiple R-squared: 0.6047, Adjusted R-squared: 0.6039 # F-statistic: 746.6 on 1 and 488 DF, p-value: < 2.2e-16 <pre>
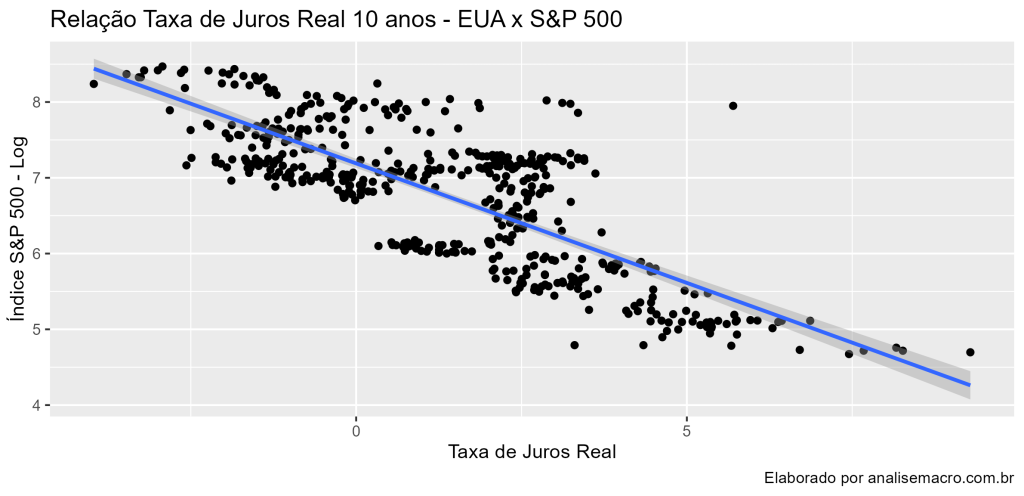
</pre> ## Gráfico de Dispersão ggplot(all_data, aes(x = real_int, y = price_adjusted))+ geom_point()+ geom_smooth(method = 'lm')+ labs(title = "Relação Taxa de Juros Real 10 anos - EUA x S&P 500", caption = "Elaborado por analisemacro.com.br", x = "Taxa de Juros Real", y = "Índice S&P 500 - Log") <pre>
Percebemos que há uma forte relação negativa. Bem como há significância estatística. Entretanto, isso realmente pode ser verdadeiro? Podemos aplicar testes no resíduos da regressão.
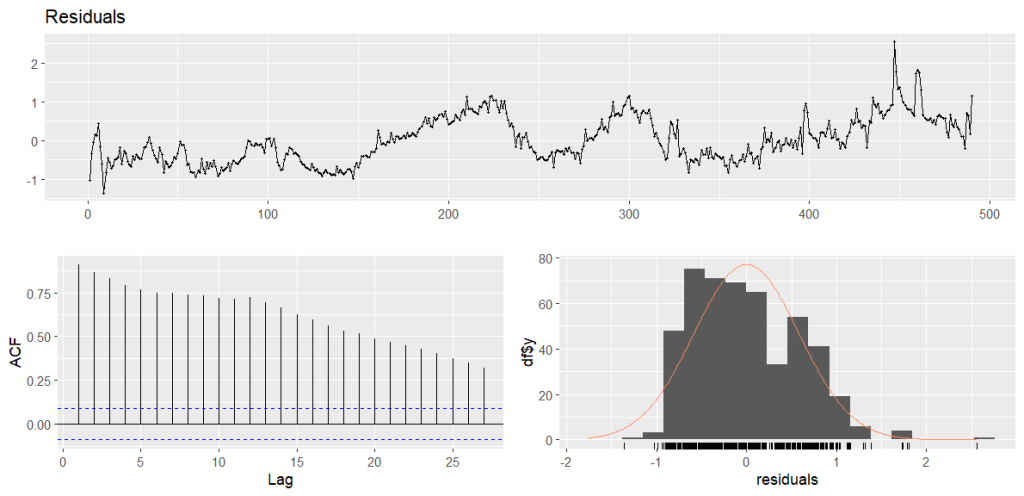
</pre> # Teste Durbin Watson lmtest::dwtest(reg_ir_sp) # Durbin-Watson test # # data: reg_ir_sp # DW = 0.16409, p-value < 2.2e-16 # alternative hypothesis: true autocorrelation is greater than 0 # Teste de estacionariedade do resíduos tseries::adf.test(x = resid(reg_ir_sp)) # Augmented Dickey-Fuller Test # # data: resid(reg_ir_sp) # Dickey-Fuller = -2.6773, Lag order = 7, p-value = 0.2916 # alternative hypothesis: stationary # Analisa os resíduos forecast::checkresiduals(reg_ir_sp) # Breusch-Godfrey test for serial correlation of order up to 10 # # data: Residuals # LM test = 419.75, df = 10, p-value < 2.2e-16 <pre>
Pelo relativo alto valor do R² (60%), significância do coeficiente de regressão a 5%, além de considerar a tendência de ambas as séries, bem como suas distribuições e autocorrelação, é possível considerar que tenhamos uma regressão espúria. Isso pode ser provado através da avaliação do erros do modelo acima, por meio da estatística Durbin-Watson, da estacionária do resíduos com um teste ADF e uma avaliação gráfica.
Considerações
Apesar de encontrar relações entre as duas variáveis, não é possível afirmar que isso seja verdadeiro. Propõe-se avaliar se as séries são cointegradas, além de testar as séries em diferentes ordens de integração.
Quer saber mais?
Conheça nossa Formação em Macroeconomia Aplicada.