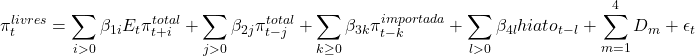O objetivo do post de hoje será criar um código em R para uma forma reduzida da Curva de Phillips com a imposição da restrição de verticalidade de longo prazo estimada com instrumentos para o Brasil. O modelo segue uma versão simplificada do apresentado pelo Boxe do RI 2018/09.
A Curva de Phillips para a inflação de preços livres do Brasil é representada por:
(1)
com a imposição da restrição de verticalidade de longo prazo:
(2)
onde é a inflação de preços livres do IPCA;
é a expectativa em t acerca da inflação do IPCA i trimestres à frente;
é a inflação do IPCA;
é uma medida da inflação importada;
é uma medida do hiato do produtos;
são Dummys de choques e
um termo de erro.
Basicamente, a inflação dos preços livres é uma função linear da inflação passada, das expectativas de inflação, do hiato do produto e da inflação importada. Os dados são trimestrais.
Para estimarmos a Curva de Phillips iremos passar por todas as etapas do processo de análise de dados utilizando o R, iremos coletar os dados, realizar os devidos tratamentos, e por fim iremos estimar a equação por meio de uma regressão em dois estágios.
Coleta e tratamento de dados
Expectativas de Inflação
Vamos começar importando os dados da expectativas de inflação do Banco de dados do Banco Central, referente ao Boletim Focus, utilizando o pacote {rbcb}. Como estamos trabalhando com variáveis trimestrais, teremos que realizar a mudança dos valores importados de mensais para a frequência menor.
# Coleta expectativa acumulada em 12 meses do IPCA - FOCUS exp_ipca <- rbcb::get_twelve_months_inflation_expectations( indic = "IPCA", end_date = Sys.Date() ) # Trimestraliza expectativa (média) exp_ipca_aux <- exp_ipca %>% dplyr::filter( base == 0, # base 0 smoothed == "S" # estatística suavizada ) %>% dplyr::group_by( date_y = lubridate::year(date), date_m = lubridate::month(date) ) %>% dplyr::summarise( mean_month = mean(median), # média mensal .groups = "drop" ) %>% dplyr::group_by( date_quarter = lubridate::make_date(year = date_y, month = date_m) %>% lubridate::quarter(with_year = TRUE) ) %>% dplyr::summarise( ipca_exp_12m = mean(mean_month), # média trimestral .groups = "drop" )
Inflação Total e de Preços Livres
A inflação total e de preços livres são importadas por meio do pacote {GetBCBData} e acumulada em 12 meses por meio da função acum_quarter criada manualmente. Além disso, há também a criação do IPCA Livres ajustados sazonalmente por meio do X 13ARIMA SEATS.
acum_quarter <- function(x){
x_fac <- 1+(x/100)
x_cum <- RcppRoll::roll_prodr(x_fac, n = 3)
x_qr <- dplyr::last((x_cum-1)*100)
return(x_qr)
}
# Coleta de dados do IPCA (cheio e livres)
dados_ipca <- GetBCBData::gbcbd_get_series(
id = c(
"ipca_total"
= 433,
# códigos do SGS/BCB
"ipca_livres" = 11428
),
first.date
= "1998-01-01",
format.data = "wide",
use.memoise = FALSE
) %>%
dplyr::mutate(date_quarter = lubridate::quarter(`ref.date`, with_year = TRUE)) %>%
dplyr::group_by(date_quarter) %>%
dplyr::summarise(
dplyr::across(
c(ipca_total, ipca_livres),
~acum_quarter(.x)
),
.groups = "drop"
)
# Ajustar sazonalmente IPCA Livres
ipca_livres_sa <- dados_ipca %>%
tidyr::drop_na() %>%
dplyr::select(date_quarter, ipca_livres) %>%
dplyr::filter(date_quarter >= 1999.4) %>%
dplyr::mutate(
date = lubridate::yq(date_quarter) %>%
tsibble::yearquarter()
) %>%
tsibble::as_tsibble(index = "date") %>%
fabletools::model(x11 = feasts::X_13ARIMA_SEATS(ipca_livres ~ x11())) %>%
fabletools::components() %>%
dplyr::as_tibble() %>%
dplyr::mutate(
date_quarter = lubridate::quarter(date, with_year = TRUE),
ipca_livres_sa = season_adjust
) %>%
dplyr::select(date_quarter, ipca_livres_sa)
# Juntar com dados do IPCA
dados_ipca <- dplyr::left_join(dados_ipca, ipca_livres_sa, by = "date_quarter")
IC-Br
O Indicador IC-Br é utilizado como medida da inflação importada. É importado através do banco de dados do Banco Central por meio do pacote {GetBCBData}.
acum_ic <- function(x){
x_diff <- log(x/dplyr::first(x))*100
x_acum <- dplyr::last(x_diff)
return(x_acum)
}
dados_ic <- GetBCBData::gbcbd_get_series(
id = c("ic_br" = 27574), # códigos do SGS/BCB
first.date = "1998-01-01",
format.data = "wide",
use.memoise = FALSE
) %>%
dplyr::mutate(date_quarter = lubridate::quarter(`ref.date`, with_year = TRUE)) %>%
dplyr::group_by(date_quarter) %>%
dplyr::summarise(ic_br = acum_ic(ic_br), .groups = "drop")
Hiato do Produto
Para o Hiato do produto, é utilizado os dados criados pela IFI - Instituição Fiscal Independente. Realiza-se o download e a importação da planilha com seus devidos tratamentos.
hiato <- rio::import( file = paste0( "https://www12.senado.leg.br/ifi/dados/arquivos/", "estimativas-do-hiato-do-produto-ifi/at_download/file" ), format = "xlsx", sheet = "Hiato do Produto", skip = 1 ) %>% dplyr::mutate( date_quarter = lubridate::quarter(`Trim-Ano`, with_year = TRUE), hiato = `Hiato` * 100 ) %>% dplyr::select(date_quarter, hiato)
Por fim, realiza-se a junção de todos os data frames criados anteriormente em um só, bem como cria-se as defasagens e o dummys.
dados_reg <- purrr::reduce(
.x = list(dados_ipca, dados_ic, hiato, exp_ipca_aux),
.f = dplyr::left_join,
by = "date_quarter"
) %>%
dplyr::mutate(
ipca_total_lag1 = dplyr::lag(ipca_total, 1),
ipca_total_lag2 = dplyr::lag(ipca_total, 2),
ipca_livres_lag1 = dplyr::lag(ipca_livres, 1),
ipca_livres_lag2 = dplyr::lag(ipca_livres, 2),
ipca_livres_sa_lag1 = dplyr::lag(ipca_livres_sa, 1),
ic_lag1 = dplyr::lag(ic_br, 1),
ic_lag2 = dplyr::lag(ic_br, 2),
hiato_lag1 = dplyr::lag(hiato, 1),
hiato_lag2 = dplyr::lag(hiato, 2),
hiato_lag3 = dplyr::lag(hiato, 3),
hiato_lag4 = dplyr::lag(hiato, 4),
ipca_exp_12m_lag1 = dplyr::lag(ipca_exp_12m, 1),
ipca_exp_12m_lag2 = dplyr::lag(ipca_exp_12m, 2),
ipca_exp_12m_lag3 = dplyr::lag(ipca_exp_12m, 3),
ipca_exp_12m_lag4 = dplyr::lag(ipca_exp_12m, 4),
ipca_exp_12m_lead1 = dplyr::lead(ipca_exp_12m, 1),
ipca_exp_12m_lead2 = dplyr::lead(ipca_exp_12m, 2),
ipca_exp_12m_lead3 = dplyr::lead(ipca_exp_12m, 3),
quarter = stringr::str_sub(date_quarter, start = 6, end = 6) %>% as.numeric(),
quarter_1 = dplyr::if_else(quarter == 1, 1, 0),
quarter_2 = dplyr::if_else(quarter == 2, 1, 0),
quarter_3 = dplyr::if_else(quarter == 3, 1, 0),
quarter_4 = dplyr::if_else(quarter == 4, 1, 0),
d_lula = dplyr::if_else(date_quarter %in% c(2002.3, 2003.1, 2003.2), 1, 0),
d_subprime = dplyr::if_else(date_quarter == 2008.2, 1, 0),
d_dilma = dplyr::if_else(date_quarter == 2015.2, 1, 0),
d_covid = dplyr::if_else(date_quarter %in% c(2020.3, 2020.4), 1, 0)
) %>%
dplyr::filter(date_quarter >= 2002.1) %>%
tidyr::drop_na() %>%
as.data.frame()
Modelagem
Para estimar o modelo, utiliza-se o pacote {systemfit} para aplicar uma Regressão Linear em dois estágios.
# Instrumentos (expressão de fórmula) instrumentos <- ~ ipca_livres_lag1 + ipca_exp_12m_lead2 + ipca_total_lag1 + ic_lag1 + hiato_lag1 + d_lula + d_dilma + d_covid + quarter_1 + quarter_2 + quarter_3 # Restrição de longo prazo restricao <- "eq1_ipca_exp_12m + eq1_ipca_total_lag1 + eq1_ic_lag1 = 1" # Estimação eq_phillips <- systemfit::systemfit( formula = ipca_livres ~ -1 + ipca_exp_12m + ipca_total_lag1 + ic_lag1 + hiato_lag1 + d_lula + d_dilma + d_covid + quarter_1 + quarter_2 + quarter_3, method = "2SLS", data = dados_reg, inst = instrumentos, restrict.matrix = restricao )
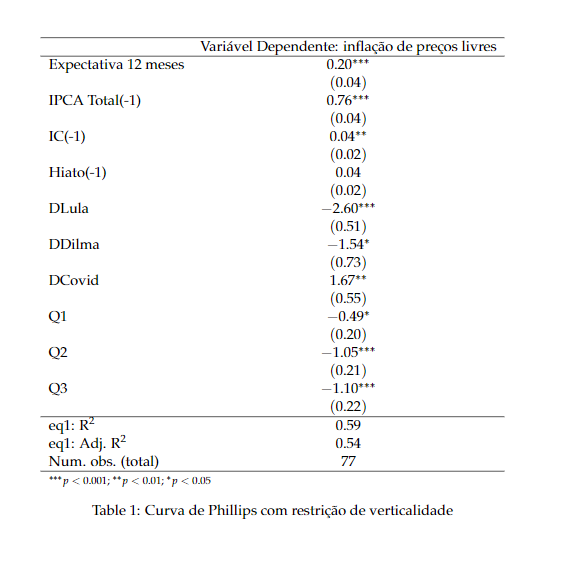
O resultado do modelo apresentado no atual momento é dado pela seguinte imagem:
_____________________________________
Quer saber mais?
Veja a nossa trilha de Macroeconomia Aplicada.