As empresas em geral são expostas a diferentes tipos de risco, portanto, é de interesse saber qual o montante monetário a companhia pode perder em um determinado horizonte de tempo. Para tanto, é possível utilizar o VaR e CVaR, que estimam essa probabilidade de perda monetária. No post de hoje, iremos aprender a como calcular essas medidas utilizando o Python por meio de exemplos reais.
Riscos
Empresas em geral sofrem de diferentes tipos de risco, mas usualmente são mais expostas a três classes de risco: operacional, estratégico e financeiro. Os riscos financeiros estão ligados às variações de variáveis financeiras (juros, câmbio, entre outros) e que implicam perdas financeiras.
Os riscos financeiros podem ser classificados em vários tipos, como operacional, de crédito, de liquidez, portanto, estes são os de maiores interesse para o mercado financeiro, pois representam perdas potenciais associadas ao comportamento do mercado.
Value At Risk
O Value at Risk é uma medida da variação potencial máxima do valor de um ativo (ou carteira), sobre um período pré-fixado, com dada probabilidade. Em outras palavras, expressa a perda monetária, com probabilidade p, sobre um horizonte h fixado.
E como calcular o VaR? Existem diversos métodos, com os respectivos parâmetros da medida estimados por diferentes modelos, entretanto, trabalharemos aqui com um método bastante simples, o Historical VaR.
Historical VaR
O VaR Histórico calcula a perda monetária com base em um quantil dos retornos negativos passados. Esse método é útil quando se obtém um nível grande de dados passados, ou seja, por definição é uma analise ex-post da distribuição de retorno.
Em que é o quantil empírico dos retornos negativos da série. Esse quantil é estabelecido de acordo o nível de confiança, usualmente 95% e 99%.
Vamos calcular o Historical VaR com o Python. Utilizaremos os retornos do preço de fechamento diários de quatro empresas escolhidas aleatoriamente. No código abaixo, realiza-se a importação dos dados e o calculo dos retornos.
# Importa as bibliotecas
import numpy as np
import pandas as pd
from pandas_datareader import data as pdr
!pip install yfinance
import yfinance as yf
yf.pdr_override()
from matplotlib import pyplot as plt
plt.style.use("seaborn")
# Busca os preços das ações ## Define as ações assets = ['ITUB4.SA', 'PETR4.SA', 'VALE3.SA', 'BRFS3.SA'] ## Define a data início start = '2021-01-01' end = "2022-11-01" # Busca os preços ajustados prices = pdr.get_data_yahoo(assets, start = start, end = end)['Close'] # Calcula os retornos e retira dados faltantes returns = prices.pct_change().dropna() weights = np.ones((4, 1)) # Normaliza para obter os pesos (iguais) weights = weights / np.sum(weights) # Calcula o retorno do portfolio returns_portfolio = returns.assign(portfolio = returns.dot(weights))
Uma vez que temos os retornos, podemos calcular o VaR Histórico tanto dos ativos individualmente, quanto dos ativos em conjunto, em forma de um portfólio, que para tanto, definimos com pesos iguais dos ativos.
# Cria a função para calcular o VaR def value_at_risk(valor_investido, retornos, alpha = 0.95): # Calcula o percentil de perda e multiplica pelo valor investido return np.percentile(retornos, 100 * (1-alpha)) * valor_investido # Define o valor investido valor_investido = 1000 # Calcula o VaR com base nos retornos históricos do portfolio portfolio_var = value_at_risk(valor_investido = valor_investido, retornos = returns_portfolio['portfolio']) # Transforma em retornos portfolio_var_return = portfolio_var / valor_investido
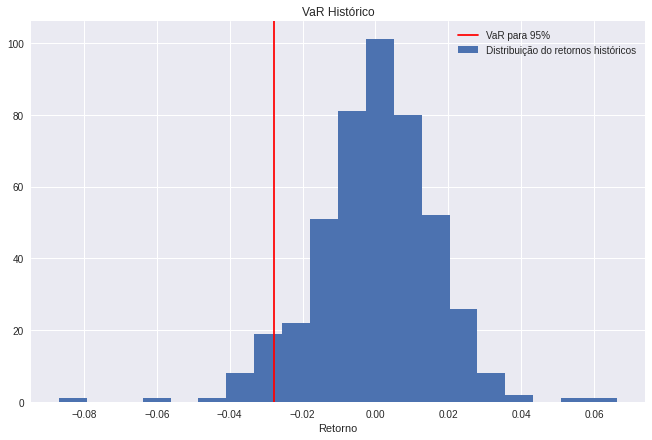
Agora podemos visualizar cada resultado (no caso do escolhido, o do portfolio) e entender por meio de um histograma a distribuição dos retornos e onde o VaR histórico reside.
# Plota a distribuição e os retornos
plt.figure(figsize = (11,7))
plt.hist(returns_portfolio['portfolio'].values, bins=20)
plt.axvline(portfolio_var_return, color='red', linestyle='solid');
plt.legend(['VaR para 95%', 'Distribuição do retornos históricos'])
plt.title('VaR Histórico');
plt.xlabel('Retorno');
Conditional Value at Risk
O CVar é considerado como se fosse uma melhoria do VaR, devido ao fato de que diferente do VaR, que considera uma distribuição normal dos dados históricos do retorno, considera não uma distribuição pré-estabelecido, mas sim dos dados empiricos. É conhecido também como Expected Shortfall (ES), devido ser uma expectativa de diferentes perdas possíveis maiores que o VaR.
O CVaR é uma estimativa das perdas esperadas, calculado com base no piores 1 -x% dos cenários. Define-se o CVaR como
Agora vamos calcular o CVaR com o Python. Seguindo o mesmo conjunto de dados do Historical VaR , definimos a construção do CVaR como:
# Cria a função do CVAR def cvar(valor_investido, retornos, alpha = 0.95): var = value_at_risk(valor_investido, retornos, alpha) # Get back to a return rather than an absolute loss var_pct_loss = var / valor_investido return valor_investido * np.nanmean(returns[returns < var_pct_loss])
E o resultado empírico com dado montante R$ 1000 investido será:
# Calcula o CVaR portfolio_cvar = cvar(valor_investido, returns_portfolio['portfolio'], alpha = 0.95) # Transforma o CVaR em retornos portfolio_cvar_returns = portfolio_cvar / valor_investido
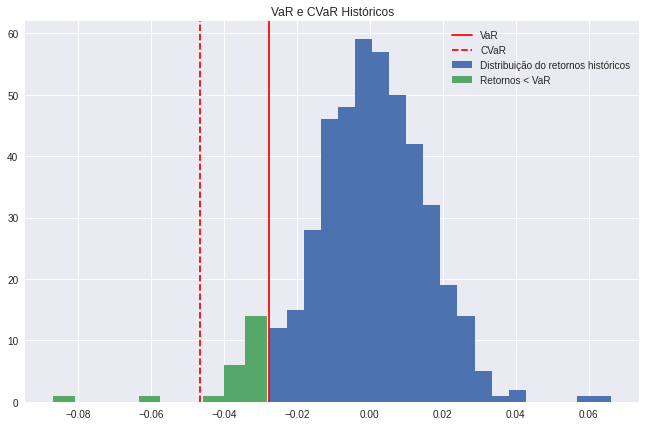
Podemos comparar as duas medidas visualmente por meio de um histograma:
# Retira os valores dos retornos para o plot do histograma
values_returns = returns_portfolio['portfolio'].values
# Plota a distribuição dos retornos, o VaR e o CVaR
plt.figure(figsize = (11,7))
plt.hist(values_returns[values_returns > portfolio_var_return], bins=20)
plt.hist(values_returns[values_returns < portfolio_var_return], bins=10)
plt.axvline(portfolio_var_return, color='red', linestyle='solid');
plt.axvline(portfolio_cvar_returns, color='red', linestyle='dashed');
plt.legend(['VaR',
'CVaR',
'Distribuição do retornos históricos',
'Retornos < VaR'])
plt.title('VaR e CVaR Históricos');
______________________________________
Quer saber mais?
Veja nosso curso de Python para Investimentos.