Vamos continuar a série de postagens sobre como construir um Dashboard de métricas relacionadas a avaliação de ações e construção de um Portfolio de investimentos no Python. Trazemos nessa semana um componente importante para avaliação do risco: Capital Asset Pricing Model (CAPM).
O que é o CAPM?
O CAPM (Capital Asset Pricing Model) é um modelo financeiro utilizado para estimar o retorno esperado de um ativo financeiro. Ele foi desenvolvido com base na ideia de que o retorno de um ativo financeiro é composto por dois componentes: o retorno livre de risco e o prêmio de risco.
O retorno livre de risco é o retorno que um investidor pode obter sem correr risco algum, geralmente associado a investimentos em títulos públicos. O prêmio de risco, por sua vez, é a compensação que um investidor deve receber para correr o risco de investir em um ativo financeiro mais arriscado, como ações.
O CAPM utiliza a relação entre o risco e o retorno para determinar o retorno esperado de um ativo financeiro. Ele assume que o risco de um ativo pode ser medido pelo seu beta, que é uma medida de volatilidade relativa do ativo em relação ao mercado.
De acordo com o CAPM, o retorno esperado de um ativo financeiro é igual ao retorno livre de risco mais um prêmio de risco proporcional ao seu beta. Esse prêmio de risco é calculado multiplicando o beta do ativo pela diferença entre o retorno esperado do mercado (ou retorno da carteira de mercado) e o retorno livre de risco.
Estimando o CAPM
Com o retorno da carteira de mercado representando o risco sistemático, chega-se a conclusão de que as variações do portfólio de mercado representaria um fator importante na variação do retorno de uma ação. Para tanto, na formulação do CAPM foi levado em conta o quanto estes retornos se relacionam, representado pelo Beta de mercado, formando então a seguinte equação calculada através de uma Regressão Linear via MQO:
em que representa o excesso de retorno de um ativo, dado pela subtração do retorno do ativo em relação ao retorno da taxa de juros livre de risco.
o excesso de retorno do portfolio de mercado, sendo representado pela diferença do retorno de mercado e do retorno da taxa de juros livre de risco.
é o coeficiente da regressão que demonstrará o efeito da variação do excesso de retorno do mercado no excesso de retorno do ativo.
é o erro da regressão.
O objetivo então é obter as taxas de retorno do ativo, do portfólio de mercado e da taxa de juros livre de risco e estimar o Beta de mercado (coeficiente de regressão) .
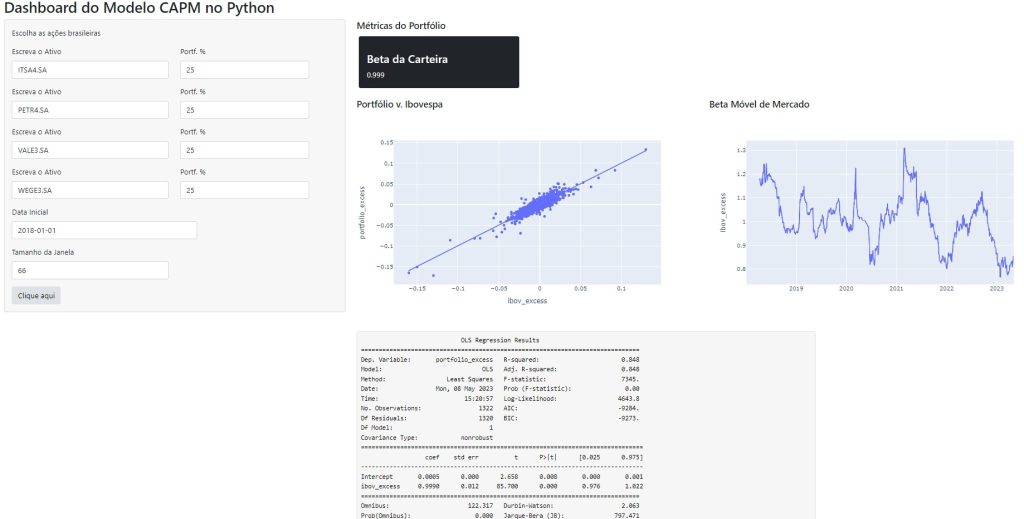
Dashboard do Modelo CAPM no Python
Para facilitar todo o trabalho de estimar o CAPM, é possível criar um Dashboard, que automatiza todo o processo de coleta, tratamento, e a visualização de dados. No Dashboard abaixo, o processo de coleta de dados financeiros foi feito por meio da biblioteca yfinance. O Dashboard é construído no ambiente da biblioteca Shiny e os gráficos construídos por meio do Plotly.
Para acessar o Dashboard construído pela Análise Macro, acesse-o pelo seguinte link: Dashboard do Modelo CAPM no Python
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas