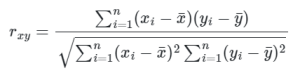A análise de correlação desempenha um papel importante na análise e ciência de dados, dado que pode ser útil como indicativo de relação previsível entre variáveis, o que pode ser explorado de forma prática. No entanto, há muita confusão sobre sua interpretação e a aplicação em situações com dados reais pode ser, às vezes, desastrosa.
Neste artigo, vamos apresentar o conceito de correlação na estatística, avaliar sua aplicabilidade no mundo real, verificar como estimar e interpretar o coeficiente de correlação e, por fim, vamos ver como aplicar a análise de correlação com dados macro-financeiros do Brasil, usando as linguagens de programação R e Python.
O que é correlação?
Em estatística, a correlação é qualquer relação estatística, causal ou não, entre duas variáveis aleatórias. Mas o que isso significa? Em termos técnicos, a correlação entre duas variáveis denota o grau em que as variáveis estão linearmente relacionadas. Ou seja, é uma medida de quanto as variáveis se relacionam em termos de força e direção.
Alguns possíveis exemplos de correlação são:
- Altura dos pais vs. altura dos filhos
- Preço do produto vs. quantidade do produto (curva de demanda)
- Tamanho dos sapatos vs. quantidade de filmes assistidos
- Taxa básica de juros vs. taxa de inflação
- Taxa de câmbio vs. volume de exportação
Note que, dos exemplos acima, podemos considerar razoável pensar que algumas correlações podem ser mais fortes do que outras e que algumas correlações “não façam sentido”, ou seja, sejam nulas. Exploraremos mais essa intuição na seção de interpretação do coeficiente de correlação adiante.
Também é importante notar que a correlação estatística aqui mencionada só mede a relação linear entre duas variáveis. Variáveis que se relacionam de forma não linear (i.e., tempo e crescimento populacional) não podem ser captadas corretamente por medidas de correlação linear, sendo necessário utilizar medidas apropriadas para analisar essas relações.
Prós e contras: quando usar e quando não usar correlação?
Nem tudo na vida é fácil e, apesar da simplicidade da análise de correlação, ao analisar o relacionamento entre duas variáveis usando medidas de correlação linear precisamos ter cuidado. Se usada incorretamente, a análise de correlação deixa de ser simples, rápida e visualmente apelativa e passa a ser um monstro atacando relações não lineares ou cuspindo relações causais.
A seguir vamos pontuar a aplicabilidade da análise de correlação, contextualizando para quando devemos decidir usá-la ou não.
Use análise de correlação para:
- Explorar relacionamentos: a análise de correlação ajuda a determinar a força e a direção de uma relação linear entre variáveis, através de uma medida de coeficiente numérico.
- Seleção de variáveis: a análise de correlação pode ajudar em tarefas de modelagem preditiva para identificar variáveis que são fortemente correlacionadas com uma variável alvo.
- Tomada de decisão: a análise de correlação pode ajudar com informações úteis e insights para o processo de tomada de decisão na análise entre duas variáveis.
Não use análise de correlação para:
- Causalidade: o coeficiente da análise de correlação não deve ser interpretado como uma evidência de causalidade entre as variáveis.
- Relações não lineares: o coeficiente de correlação linear mede relações lineares entre variáveis e não deve ser usada para relacionamentos não lineares.
- Valores extremos: a análise de correlação é sensível a valores extremos (outliers), que podem produzir um coeficiente indicando uma forte relação mesmo que as variáveis não sejam lineares.
Note que há exceções para esses casos de uso, devendo o contexto, o problema e o objetivo da análise ser sempre considerado ao aplicar a análise de correlação. Não use a lista acima cegamente!
Como calcular a correlação entre duas variáveis?
Existe mais de um método diferente de medir a relação entre duas variáveis, mas o mais conhecido e utilizado é o coeficiente de correlação de Pearson.
Esse método só mede a relação linear e é comumente denotado com os símbolos p (rho) ou r para medir o grau de correlação. Ele pode ser calculado pela divisão da covariância das duas variáveis pelo produto dos seus desvios padrão.
A fórmula matemática para calcular o coeficiente de correlação amostral de Pearson é:
onde:
n é o nº total de observações na amostra.
x_i e y_i são os valores individuais das duas variáveis.
x_barra e y_barra são as médias amostrais de x e y, respectivamente.
Como interpretar o valor da correlação?
O coeficiente de correlação de Pearson pode assumir valores no intervalo entre -1 e + 1, inclusive. Isso implica que a correlação entre duas variáveis pode ser negativa, positiva ou nula, além de indicar, informalmente, a força da relação linear. Formalmente, qualquer valor do coeficiente entre os extremos indica apenas o grau de dependência linear entre as variáveis.
Note que nenhuma referência sobre causalidade entre variáveis foi feita no parágrafo anterior. O motivo é que a análise de correlação não deve ser usada como evidência de relação causa-efeito entre variáveis. Esse é um grande erro que muitas pessoas cometem (basta navegar em qualquer rede social para verificar), que acontece há muito tempo e é motivo de piada para quem estuda ou trabalha com estatística, econometria ou aprendizado de máquina.
Um guia prático comumente utilizado para interpretar o coeficiente de correlação de Pearson é o que se segue:
- ±0.9 a ±1 indica correlação muito forte
- ±0.7 a ±0.9 indica correlação forte
- ±0.5 a ±0.7 indica correlação moderada
- ±0.5 a ±0.3 indica correlação fraca
- ±0.3 a 0 indica correlação desprezível ou nula
Exemplo prático: correlação entre variáveis macro-financeiras
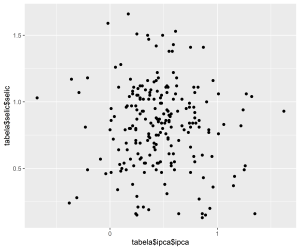
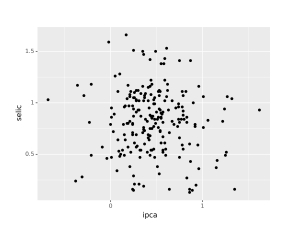
Para fixar o conhecimento de forma aplicada usando ferramentas práticas de linguagem de programação, abaixo calculamos o coeficiente de correlação de Pearson entre as variáveis “taxa de juros Selic” e “taxa de inflação IPCA”, período 2005 a 2023. A fonte dos dados é o BCB e o IBGE.
R
Python
O procedimento pode ser feito com funções prontas de bibliotecas ou com a implementação da fórmula vista acima. Recomenda-se usar sempre as funções prontas, dado que a implementação exposta é limitada e tem finalidade didática.
Note que a correlação encontrada é negativa, mas muito próxima a zero, ou seja, desprezível. Isso vai de encontro com a teoria econômica, porém essa análise de correlação é simples demais para investigar com profundidade a real relação entre essas variáveis.
Conclusão
Neste artigo, apresentamos o conceito de correlação na estatística, avaliamos sua aplicabilidade no mundo real, verificamos como estimar e interpretar o coeficiente de correlação e, por fim, aplicamos a análise de correlação com dados macro-financeiros do Brasil, usando as linguagens de programação R e Python.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
Referências
Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. Saraiva.
Mukaka, M. M. (2012). A guide to appropriate use of correlation coefficient in medical research. Malawi medical journal, 24(3), 69-71.