Método dos Momentos Generalizados

De modo a complementar o conhecimento sobre modelos utilizados no âmbito da modelagem macroeconômica, vamos mostrar agora um método que pode ser considerado uma generalização de diversos outros métodos de estimação, tais como mínimos quadrados, variáveis instrumentais e máxima verossimilhança. Vamos realizar uma introdução ao Método dos Momentos Generalizado (GMM) e demonstrar o seu uso através de um exemplo no Python.

Enquanto, como vimos, as propriedades do estimador de mínimos quadrados depende da exogeneidade dos regressores, o Método dos Momentos Generalizado (GMM) é muito mais flexível dado que ele requer apenas algumas premissas relacionadas a condições de momento. Em macroeconomia, por exemplo, isso permite estimar um modelo estrutural equação por equação.

O GMM é uma abordagem flexível que permite estimar parâmetros desconhecidos usando informações sobre os momentos das variáveis aleatórias observadas.

A ideia principal do GMM é encontrar os valores dos parâmetros que tornam os momentos teóricos calculados a partir do modelo estatístico mais próximos possível dos momentos empíricos observados nos dados. Isso é feito minimizando uma função de distância entre os momentos empíricos e teóricos.

Os momentos são estatísticas descritivas das distribuições das variáveis, como a média, a variância e assim por diante.

Para ilustrar, considere que desejamos estimar um vetor de parâmetros desconhecidos, denotado por $\theta_0 \in \mathbb{R}$ , em um modelo estatístico. Para fazer isso, utilizamos um vetor de condições de momento incondicionais. Essas condições são expressas pela equação:

$E \left [ g(\theta_0, x_i) \right ] = 0,$

onde $g(\theta_0, x_i)$ é uma função que relaciona os parâmetros $\theta_0$ com os dados observados $x_i$ O termo $E[]$ representa o operador de expectativa matemática, ou seja, estamos considerando a média teórica da função $g(\theta_0, x_i)$ .

Essa equação indica que, quando os parâmetros $\theta_0$ estão corretamente especificados, a média teórica das funções $g(\theta_0, x_i)$ ) é igual a zero. Em outras palavras, os momentos teóricos calculados com os parâmetros corretos devem coincidir com os momentos empíricos observados nos dados.

Para que o GMM seja válido e produza estimativas consistentes dos parâmetros, é necessário que $\theta_0$ seja a solução única para a equação $E \left [ g(\theta_0, x_i) \right ] = 0$ e também pertença a um espaço compacto. A solução única garante que as estimativas sejam precisas, enquanto o espaço compacto garante que as estimativas sejam bem definidas dentro de um intervalo limitado.

De modo a ilustrar, considere que queremos estimar um vetor de parâmetros $\theta_0 \in \mathbb{R}$ de um modelo baseado no seguinte vetor $q \times 1$ de condições de momento incondicionais, isto é,

$E \left [ g(\theta_0, x_i) \right ] = 0,$

onde $x_i$ é um vetor de dados de corte transversal, de séries temporais ou de ambos.

De modo que o GMM possa produzir estimativas consistentes a partir das condições acima, $\theta_0$ precisa ser a solução única para $E \left [ g(\theta, x_i) \right ] = 0$ e ser um elemento de um espaço compacto.

Algumas suposições adicionais sobre momentos mais elevados da função $g(\theta, x_i)$ também são necessárias no Método dos Momentos Generalizado (GMM). No entanto, essas suposições não impõem nenhuma restrição específica sobre a distribuição dos dados $x_i$ , exceto em relação ao grau de dependência das observações quando se trata de um vetor de séries temporais.

Diversos métodos tais como mínimos quadrados, máxima verossimilhança ou variáveis instrumentais podem ser vistos como baseados em algumas condições de momento, o que faz deles um caso especial do GMM.

Vamos considerar um exemplo com um modelo linear simples. Suponha que temos uma equação $y = X \beta + \varepsilon$ , onde $y$ é a variável dependente que queremos prever, $X$ é uma matriz de variáveis independentes, $\beta$ é um vetor de parâmetros desconhecidos e $\varepsilon$ é o termo de erro.

Para estimar os parâmetros $\beta$ usualmente utiliza-se dos mínimos quadrados ordinários (OLS). A ideia é encontrar a melhor estimativa de $\beta$ que minimize a soma dos quadrados dos resíduos, ou seja, as diferenças entre os valores observados de $y$ e os valores previstos por $X \beta$ .

A estimativa de $\beta$ , denotada por $\hat{\beta}$ , é encontrada resolvendo o problema de minimização $min_{\beta} \left \| u \right \|^2$ , onde $u$ é o vetor de resíduos. Em outras palavras, procuramos o valor de $\beta$ que torna os resíduos o mais pequeno possível.

A condição de primeira ordem para essa minimização é dada pela equação:

(1) $\begin{align*} \frac{1}{n} X^{'} u(\beta) = 0, \end{align*}$

Essa equação é uma versão simplificada da condição de momento. Ela indica que a média dos produtos entre as variáveis independentes $x_i$ e os resíduos $u_i$ , ponderada pela matriz $x^{'}$ , deve ser igual a zero. Isso significa que os momentos teóricos calculados a partir dos dados $X$ e dos resíduos devem ser iguais a zero.

Essa equação é a base do método dos mínimos quadrados ordinários (OLS) e pode ser vista como uma forma simplificada do Método dos Momentos Generalizado (GMM) para esse caso específico de um modelo linear.

Quando lidamos com um problema de endogeneidade nas variáveis explicativas $X$ , o que significa que há uma relação entre $X$ e o termo de erro $u$ , e portanto que $E(X_i u_i) \neq 0$ , o método de variáveis instrumentais é comumente utilizado para resolver esse problema.

O método de variáveis instrumentais substitui a matriz $X$ por uma matriz de instrumentos $H$ . Essa matriz de instrumentos é escolhida de forma que esteja correlacionada com $X$ , ou seja, compartilhe alguma relação com as variáveis explicativas originais. Além disso, é importante que a matriz de instrumentos $H$ não esteja correlacionada com o termo de erro $u$ .

Essas propriedades permitem que o modelo seja estimado utilizando condições de momento condicionais ou não condicionais. As condições de momento condicionais são expressas por $E(u_i|H_i) = 0$ , o que significa que a média condicional do termo de erro $u$ dado os instrumentos $H$ é igual a zero.

Por outro lado, as condições de momento não condicionais são dadas por $E(u_i H_i) = 0$ , onde o produto entre o termo de erro $u$ e os instrumentos $H$ tem uma média igual a zero.

Em geral, dizemos que o termo de erro $u$ é ortogonal ao conjunto de informações $I$ , representado por $E(u_i|I_i) = 0$ . Isso implica que os instrumentos $H$ são um vetor contendo funções de qualquer elemento em $I$

Na presença de problema de endogeneidade para as variáveis explanatórias $X$ , o que implica que $E(X_i u_i) \neq 0$ , o método de variáveis instrumentais é usalmente utilizado, como vimos acima. Ele resolve o problema de endogeneidade ao substituir $X$ por uma matriz de instrumentos $H$ , que é requerida ser correlacionada com $X$ e não correlacionada com $u$ . Essas propriedades permitem que o modelo seja estimado pelas condições de momento condicionais $E(u_i|H_i) = 0$ ou isso implica condições de momento não condicionais $E(u_i H_i) = 0$ . Em geral, nós dizermos que $u_i$ é ortogonal ao conjunto de informação $I_i$ ou que $E(u_i|I_i) = 0$ o que implica que $H_i$ é um vetor contendo funções de qualquer elemento de $I_i$ .

No contexto do GMM, quando não temos nenhuma suposição específica sobre a matriz de covariância do termo de erro $u$ , o método de variáveis instrumentais é equivalente ao GMM. Isso significa que podemos usar o GMM para estimar o modelo quando temos endogeneidade nas variáveis explicativas $X$ .

Ao aplicar o método de variáveis instrumentais, substituímos a matriz $X$ por uma matriz de instrumentos $H$ . Nesse caso, a condição de momento para estimar o modelo é dada por:

(2) $\begin{align*} \frac{1}{T} H^{'} u(\beta) = 0. \end{align*}$

Essa equação estabelece que a média dos produtos entre os instrumentos $H$ e o vetor de resíduos $u$ , ponderada pela matriz $H^{'}$ , deve ser igual a zero.

Quando temos a condição $E(X_i u_i) = 0$ satisfeita, o método de mínimos quadrados generalizados (GLS) também é um método equivalente ao GMM. Nesse caso, o GLS é capaz de estimar o modelo sem fazer suposições específicas sobre a matriz de covariância do termo de erro u.

Um último ponto a ressaltar sobre GMM é que ainda que as estimativas produzidas por ele sejam facilmente tidas como consistentes, eficientes e não viesadas, isso vai depender muito da escolha das condições de momento. Isso porque, instrumentos ruins implicarão em informação ruim e, portanto, baixa eficiência.

Teste J

Como expõe Bueno (2011), O Método dos Momentos Generalizado (GMM) é um método estatístico que utiliza condições de momento ponderadas para estimar um modelo. Essas condições de momento representam as restrições que os parâmetros do modelo devem satisfazer. Idealmente, se as condições de momento estiverem corretas, a média dos momentos será igual a zero.

No GMM, minimizamos uma função que representa essas condições de momento ponderadas. A função é minimizada para encontrar a estimativa dos parâmetros do modelo que melhor se ajusta aos dados. Ao minimizar essa função, obtemos um valor mínimo, que é usado para realizar um teste de superidentificação chamado "teste j".

O teste j é utilizado para avaliar se as condições de momento são estatisticamente diferentes de zero. Ele é calculado como:

$J = Tg_T (w,\theta)^{'} S^{-1} g_T (w,\theta) \sim \chi_{m-k}^{2}$

onde $T$ é o tamanho da amostra, $g_T(w, θ)$ é o vetor de momentos ponderados, $S$ é a matriz de covariância dos momentos ponderados e $\theta$ são os parâmetros do modelo. O teste j segue uma distribuição qui-quadrado com $m-k$ graus de liberdade, em que $m$ é o número de momentos e $k$ é o número de parâmetros estimados.

Se o valor calculado do teste j for maior do que o valor crítico da distribuição qui-quadrado com $m-k$ graus de liberdade, rejeitamos a hipótese de que todos os momentos são iguais a zero. Isso significa que existem momentos que não são estatisticamente iguais a zero, e podemos concluir que o modelo não se ajusta bem aos dados.

Exemplo

Para obter todo o código em Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Vamos usar como exemplo o capítulo 6 do @Cameron2010, com o dataset meps.

Os dados utilizados vêm da Pesquisa de Painel de Gastos Médicos (Medical Expenditure Panel Survey - MEPS) e incluem dados sobre gastos com medicamentos do próprio bolso (em logaritmo), características individuais, se o indivíduo estava segurado por meio de um empregador ou sindicato (uma variável endógena provável) e alguns instrumentos candidatos, incluindo a porcentagem de renda proveniente do Seguro Social, o tamanho da empresa do indivíduo e se a empresa possui várias localidades.

Código


age               Age
age2              Age-squared
black             Black
blhisp            Black or Hispanic
drugexp           Presc-drugs expense
educyr            Years of education
fair              Fair health
female            Female
firmsz            Firm size
fph               fair or poor health
good              Good health
hi_empunion       Insured thro emp/union
hisp              Hiapanic
income            Income
ldrugexp          log(drugexp)
linc              log(income)
lowincome         Low income
marry             Married
midincome         Middle income
msa               Metropolitan stat area
multlc            Multiple locations
poor              Poor health
poverty           Poor
priolist          Priority list cond
private           Private insurance
ssiratio          SSI/Income ratio
totchr            Total chronic cond
vegood            V-good health
vgh               vg or good health

Vamos verificar os dados, com base na variável dependente (ldrugexp), endógena e controles.

Código

           ldrugexp   hi_empunion        totchr        female           age  \
count  10089.000000  10089.000000  10089.000000  10089.000000  10089.000000   
mean       6.481361      0.382198      1.860938      0.577064     75.051740   
std        1.362052      0.485949      1.292858      0.494050      6.682109   
min        0.000000      0.000000      0.000000      0.000000     65.000000   
50%        6.678342      0.000000      2.000000      1.000000     74.000000   
max       10.180172      1.000000      9.000000      1.000000     91.000000   

               linc        blhisp  
count  10089.000000  10089.000000  
mean       2.743275      0.163544  
std        0.913143      0.369880  
min       -6.907755      0.000000  
50%        2.743160      0.000000  
max        5.744476      1.000000

Separamos os possíveis instrumentos e verificamos as estatísticas descritivas das variáveis.

Código

           ssiratio     lowincome        multlc        firmsz
count  10089.000000  10089.000000  10089.000000  10089.000000
mean       0.536544      0.187432      0.062048      0.140529
std        0.367818      0.390277      0.241254      2.170389
min        0.000000      0.000000      0.000000      0.000000
50%        0.504522      0.000000      0.000000      0.000000
max        9.250620      1.000000      1.000000     50.000000

Avaliamos a correlação entre a variável endógena e os instrumentos. Desejamos encontrar uma correlação significativa, visto que tal valor implica na relevância dos instrumentos.

Código

data[["hi_empunion"] + instrumentos].corr()

	hi_empunion	ssiratio	lowincome	multlc	firmsz
hi_empunion	1.000000	-0.212431	-0.116419	0.119849	0.037352
ssiratio	-0.212431	1.000000	0.253946	-0.190433	-0.044578
lowincome	-0.116419	0.253946	1.000000	-0.062465	-0.008232
multlc	0.119849	-0.190433	-0.062465	1.000000	0.187275
firmsz	0.037352	-0.044578	-0.008232	0.187275	1.000000

Para finalizar a preparação de dados, adicionamos uma constante no data frame.

Código

O primeiro modelo a ser produzido será um estimado via OLS, sem instrumentos.

Código

Em seguida, produzimos um 2sls com variáveis instrumentais.

Código

E por fim, produzimos um GMM com variáveis instrumentais. Abaixo, verificamos o resultado da estimação via GMM.

Código

                          IV-GMM Estimation Summary                           
==============================================================================
Dep. Variable:               ldrugexp   R-squared:                      0.0406
Estimator:                     IV-GMM   Adj. R-squared:                 0.0400
No. Observations:               10089   F-statistic:                    1952.6
Date:                Fri, Jun 23 2023   P-value (F-stat)                0.0000
Time:                        11:44:28   Distribution:                  chi2(6)
Cov. Estimator:                robust                                         
                                                                              
                              Parameter Estimates                              
===============================================================================
             Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
-------------------------------------------------------------------------------
const           6.8778     0.2580     26.658     0.0000      6.3722      7.3835
totchr          0.4510     0.0103     43.738     0.0000      0.4307      0.4712
female         -0.0282     0.0322    -0.8752     0.3815     -0.0913      0.0349
age            -0.0142     0.0029    -4.8773     0.0000     -0.0198     -0.0085
linc            0.0945     0.0219     4.3142     0.0000      0.0515      0.1374
blhisp         -0.2231     0.0396    -5.6344     0.0000     -0.3007     -0.1455
hi_empunion    -0.9933     0.2047    -4.8530     0.0000     -1.3944     -0.5921
===============================================================================

Endogenous: hi_empunion
Instruments: ssiratio, multlc
GMM Covariance
Debiased: False
Robust (Heteroskedastic)

Para compreender melhor o GMM, verificamos o teste j.

Código

H0: Expected moment conditions are equal to 0
Statistic: 1.0475
P-value: 0.3061
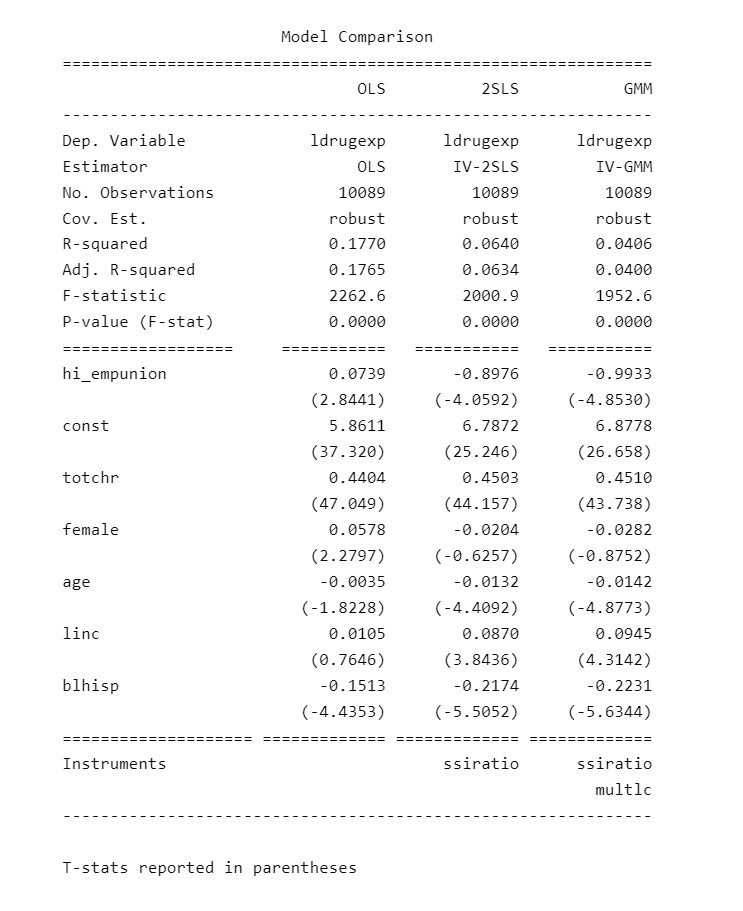
Distributed: chi2(1)

Por fim, comparamos os modelos para tirar conclusões das estimações

Código

                       Model Comparison                       
==============================================================
                               OLS          2SLS           GMM
--------------------------------------------------------------
Dep. Variable             ldrugexp      ldrugexp      ldrugexp
Estimator                      OLS       IV-2SLS        IV-GMM
No. Observations             10089         10089         10089
Cov. Est.                   robust        robust        robust
R-squared                   0.1770        0.0640        0.0406
Adj. R-squared              0.1765        0.0634        0.0400
F-statistic                 2262.6        2000.9        1952.6
P-value (F-stat)            0.0000        0.0000        0.0000
==================     ===========   ===========   ===========
hi_empunion                 0.0739       -0.8976       -0.9933
                          (2.8441)     (-4.0592)     (-4.8530)
const                       5.8611        6.7872        6.8778
                          (37.320)      (25.246)      (26.658)
totchr                      0.4404        0.4503        0.4510
                          (47.049)      (44.157)      (43.738)
female                      0.0578       -0.0204       -0.0282
                          (2.2797)     (-0.6257)     (-0.8752)
age                        -0.0035       -0.0132       -0.0142
                         (-1.8228)     (-4.4092)     (-4.8773)
linc                        0.0105        0.0870        0.0945
                          (0.7646)      (3.8436)      (4.3142)
blhisp                     -0.1513       -0.2174       -0.2231
                         (-4.4353)     (-5.5052)     (-5.6344)
==================== ============= ============= =============
Instruments                             ssiratio      ssiratio
                                                        multlc
--------------------------------------------------------------

T-stats reported in parentheses

_____________________________________
Quer aprender mais?

Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.

_______________________________________________

Referências

Bueno, R. L. S. 2011. Econometria de Séries Temporais. Editora Cengage Learning.
Cameron, Adrian Colin. 2010. Microeconometrics using Stata. Stata Press.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise de impacto fiscal sobre o dolár com Python

Resultado IBC-br - Outubro/2024

Resultado PMC - Outubro/2024

Como usar Inteligência Artificial para Ler as Atas do COPOM?

Resultado PMS - Outubro/2024

Resultado IPCA - Novembro/2024

Outros artigos relacionados

Análise de impacto fiscal sobre o dolár com Python

Usamos uma cesta de 12 moedas para construir um cenário contrafactual da taxa de câmbio após o último anúncio de pacote fiscal, com base em modelagem Bayesiana. No período, o dolár depreciou quase 5% e passou os R$ 6,15, enquanto que na ausência da intervenção a moeda deveria estar cotada em R$ 5,78.

Resultado IBC-br - Outubro/2024

A Análise Macro apresenta os resultados da IBC-br de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PMC - Outubro/2024

A Análise Macro apresenta os resultados da PMC de Outubro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Método dos Momentos Generalizados

Teste J

Exemplo

_____________________________________ Quer aprender mais?

Referências

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Outros artigos relacionados

Boletim AM

Boletim AM

_____________________________________
Quer aprender mais?