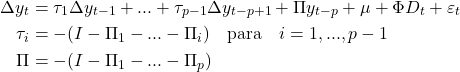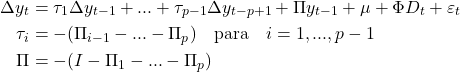Modelos Multivariados aplicados a séries temporais (Cointegração)

No post de hoje, vamos abordar os modelos lineares multivariados, apresentando conceitos importantes por meio de simulações e gráficos criados por meio das linguagens R e Python. Nosso objetivo é proporcionar uma compreensão clara e acessível desses modelos, de modo que seja fácil de entender e acompanhar. Nesta parte, apresentamos o modelo VECM.

Na análise multivariada, por suposto, a não estacionariedade das séries também pode causar problemas.

Para ilustrar, considere o exposto: Suponha duas variáveis aleatórias $X_t$ e $Y_t$ caracterizadas por um passeio aleatório. Podemos representá-las como

$X_t = X_{t-1} + \varepsilon_{Xt} \\ Y_t = Y_{t-1} + \varepsilon_{Yt}$

onde $\varepsilon_{Xt},\varepsilon_{Yt} \; \stackrel{i.i.d.}{\sim}(0,\sigma^2)$ .

Nesses termos, se estimamos o modelo dado por

$Y_t = \alpha + \beta X_t + \epsilon_t$

teremos, de modo geral, um $R^2$ relativamente alto e um $\beta$ estatisticamente significativo. Esse tipo de situação é classificada na literatura como regressão espúria, isto é, o caso onde duas séries não estacionárias estão relacionadas apenas pelo fato de ambas conterem uma tendência.

Para obter todo o código do processo de criação dos gráficos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Para ilustrar esse problema na prática, vamos fazer uso do código abaixo.

Código

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                     y1   R-squared:                       0.976
Model:                            OLS   Adj. R-squared:                  0.976
Method:                 Least Squares   F-statistic:                 2.004e+04
Date:                Wed, 28 Jun 2023   Prob (F-statistic):               0.00
Time:                        21:45:03   Log-Likelihood:                -2121.8
No. Observations:                 500   AIC:                             4248.
Df Residuals:                     498   BIC:                             4256.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         15.3585      1.409     10.902      0.000      12.591      18.126
y2             1.1885      0.008    141.567      0.000       1.172       1.205
==============================================================================
Omnibus:                       68.266   Durbin-Watson:                   0.009
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               18.342
Skew:                           0.095   Prob(JB):                     0.000104
Kurtosis:                       2.081   Cond. No.                         313.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Geramos dois processos aleatórios, $y1$ e $y2$ , e regredimos um contra o outro. O resultado foi um $R^2$ elevado e coeficiente estatisticamente significativo. Ademais, como expõe Pfaff (2008), uma regra de ouro para identificar regressões espúrias é ver o valor da Estatística Durbin-Watson, que mede autocorrelação serial.

que mede autocorrelação serial.

Código

Teste de Durbin-Watson: 0.009038763584421843

O valor da estatística é muito baixo, menor do que o $R^2$ , o que é um forte indicativo de regressão espúria. É possível lidar com esse problema, como discorre Pfaff (2008), tornando a nossa série estacionária por meio de alguma transformação, como, por exemplo, tomar a primeira diferença da série.

Em alguns casos pode, de fato, ser uma estratégia válida. Isso, entretanto, impõe algumas restrições à análise. Ao tomar a primeira diferença, o coeficiente estimado pode levar a falsas interpretações, dada a perda de informação que se tem no processo. Ademais, relações de longo prazo entre as variáveis em nível ficam perdidas.

Por isso, uma abordagem mais interessante na análise multivariada é pensar no conceito de cointegração, que expomos a seguir.

O conceito de cointegração e o modelo de correção de erros

Uma exceção ao caso de regressão espúria visto anteriormente vem à tona quando dois processos aleatórios compartilham a mesma tendência estocástica.

Para ilustrar, considere, como Verbeek (2012), duas séries integradas de ordem 1, $Y_t$ e $X_t$ , e suponha que exista uma relação linear entre elas, dada por $Y_t = \beta X_t + \epsilon_{Yt}$ .

Isso implica no fato de existir algum valor de $\beta$ tal que $Y_t - \beta X_t$ seja integrado de ordem zero, mesmo com as séries originais sendo ambas não estacionárias. Nesses casos, diz-se que as séries são cointegradas e as mesmas compartilham a mesma tendência. Observe, por suposto, que a relação entre $X_t$ e $Y_t$ poderá ser caracterizada pelo vetor $[1,-\beta]^{'}$ .

Sendo um pouco mais formal, com base em Pfaff (2008), a ideia por trás do conceito de cointegração é encontrar uma combinação linear entre duas variáveis $I(d)$ de tal sorte que isso leve a uma variável de menor ordem de integração.

Isto é, os elementos do vetor $x_t$ são ditos cointegrados de ordem $d, b$ , denominado por $x_t \sim CI(d,b)$ , se todos os elementos de $x_t$ são $I(d)$ e o vetor $\alpha (\neq 0)$ existe tal que $z_t = \alpha^{'} x_t \sim I(d-b)$ , onde $b > 0$ . O vetor $\alpha$ é então chamado cointegrante.

Para os economistas, por exemplo, esse tipo de análise permite estabelecer relações de longo prazo entre variáveis não estacionárias. O problema, passa a como estimar o vetor cointegrante e como modelar o comportamento dinâmico das variáveis $I(d)$ .

Para resolver, vamos ilustrar o método de dois passos de Engle-Granger, exposto em Pfaff (2008).

No primeiro passo, estimamos o seguinte modelo contendo variáveis não estacionárias de mesma ordem de integração

$y_t = \alpha_1 x_{t,1} + \alpha_2 x_{t,2} + \alpha_K x_{t,K} + z_t$

para $t = 1,...,T$ , onde $z_t$ é um termo de erro. O vetor cointegrante $(K+1)$ $\hat{\alpha}$ estimado é dado por $\hat{\alpha} = [1,-\hat{\alpha^{*}}]^{'}$ , onde $\hat{\alpha^{*}} = (\hat{\alpha_1},...,\hat{\alpha_K})$ .

Assim, acaso exista uma relação de cointegração entre as variáveis, $z_t$ nada mais é do que o erro em relação ao equilíbrio de longo prazo entre elas. Nesse caso, $z_t$ será necessariamente estacionário. Obs. Pelo fato de $z_t$ ser uma variável estimada, é preciso testar a presença de raiz unitária com outros valores críticos.

Se conseguirmos evidências de que $z_t$ é de fato estacionário, podemos passar adiante. O passo seguinte é especificar um modelo de correção de erros (ECM, no inglês).

Para simplificar, vamos considerar o caso bivariado, onde $y_t$ e $x_t$ são cointegradas, sendo ambas $I(1)$ . O ECM é então especificado, de forma geral, como segue

$\Delta y_t = \psi_0 + \gamma_1 \hat{z_{t-1}} + \sum_{i=1}^{K} \psi_{1,i} \Delta x_{t-i} + \sum_{i=1}^{L} \psi_{2,i} \Delta y_{t-i} + \varepsilon_{1,t}$

$\Delta x_t = \xi_0 + \gamma_2 \hat{z_{t-1}} + \sum_{i=1}^{K} \xi_{1,i} \Delta y_{t-i} + \sum_{i=1}^{L} \xi_{2,i} \Delta x_{t-i} + \varepsilon_{2,t}$

onde $\hat{z_{t}}$ é o erro do modelo estimado e $\varepsilon_{1,t}$ $\varepsilon_{2,t}$ são ruídos brancos. Nesses termos, o ECM implica que mudanças em $y_t$ são explicadas pela sua própria estória, mudanças defasadas em $x_t$ e pelos erros obtidos da relação de equilíbrio na equação de $y_t$ .

O valor do coeficiente $\gamma_1$ determina, a velocidade de ajustamento e deveria ser sempre negativo. De outra forma, o sistema poderia divergir da sua trajetória de equilíbrio de longo prazo.

Existe cointegração entre a PETR4 e PETR3?

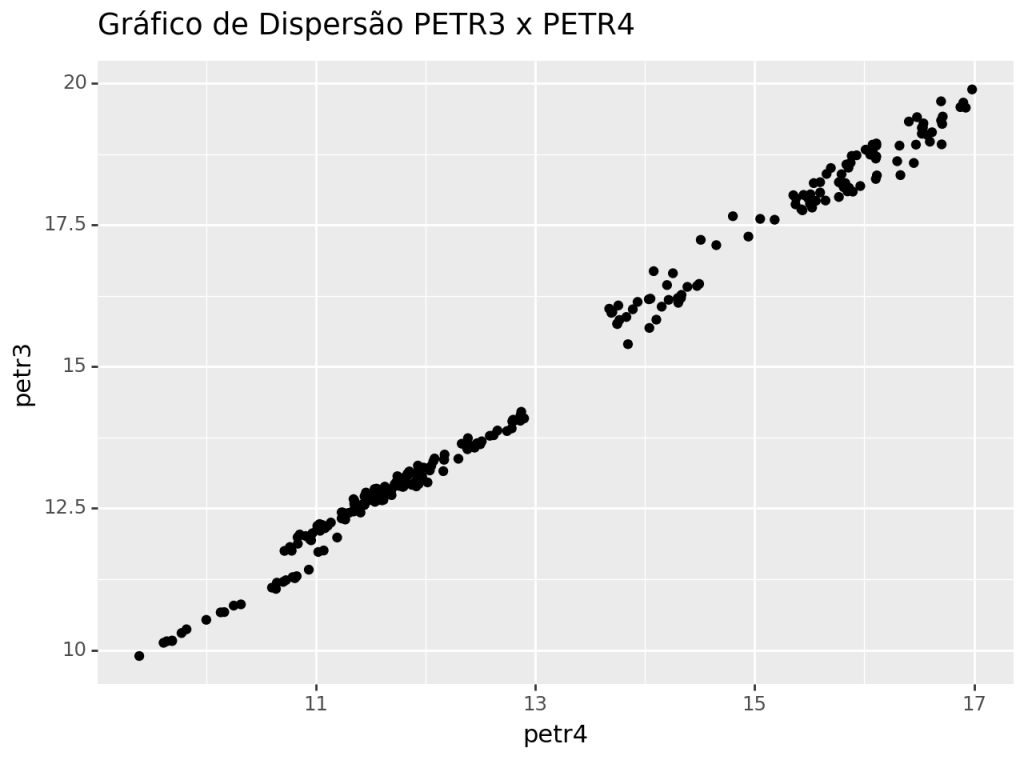
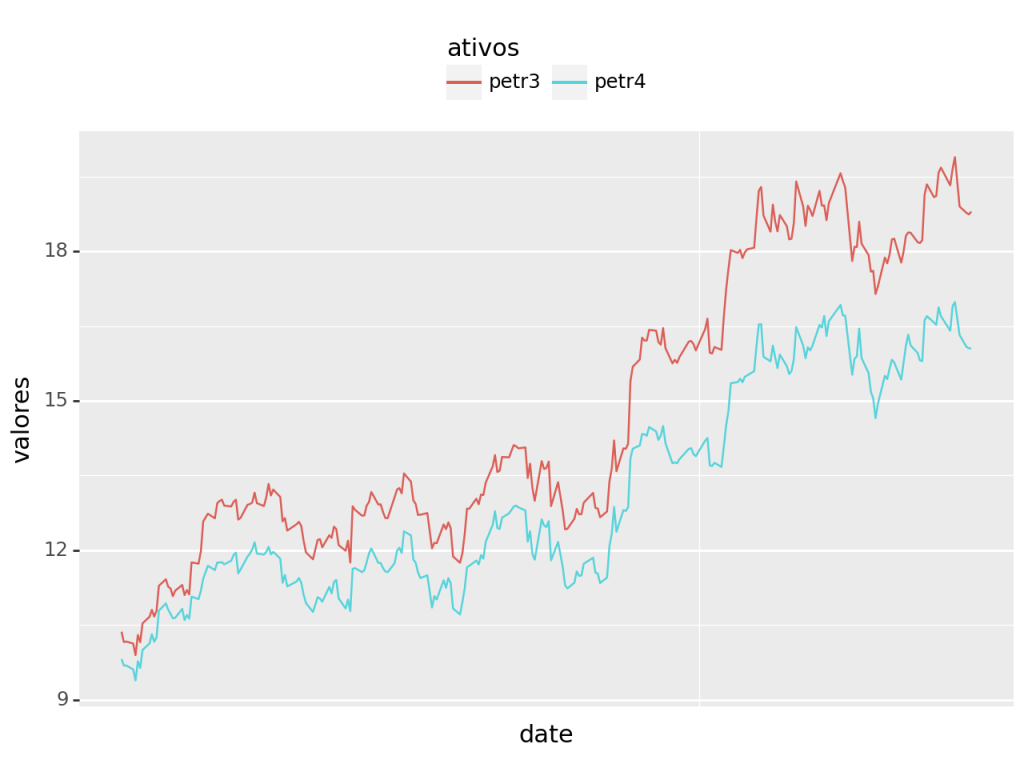
Para ilustrar a metodologia de Engle-Granger, vamos ver se podemos encontrar uma relação de cointegração entre as ações da PETR4 e PETR3 no período de 28 de março de 2021 até 28 de março de 2022. A ideia básica é a de que os preços de ambas as ações seguem uma mesma tendência estocástica, visto que possuem uma trajetória comum.

Código

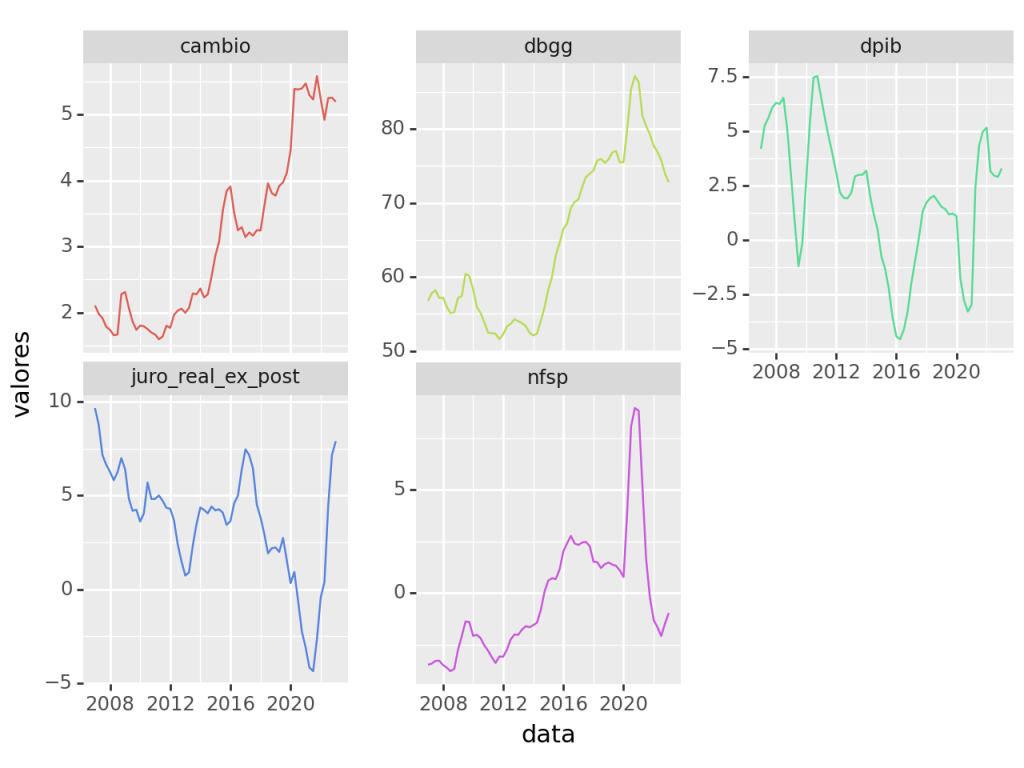
Visualizamos as séries e verificamos claramente que não são estacionárias, o que permite aplicarmos o Teste de Engle-Granger (fica ao leitor a aplicação de algum tipo de teste de estacionariedade).

Há claramente uma trajetória comum entre as séries.

Antes, podemos dar uma olhada na correlação entre as variáveis abaixo.

Podemos perceber a relação entre os preços das duas ações. Agora partimos para a estimação da regressão linear, em que petr3 ~ petr4.

Código

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  petr3   R-squared:                       0.994
Model:                            OLS   Adj. R-squared:                  0.994
Method:                 Least Squares   F-statistic:                 3.874e+04
Date:                Wed, 28 Jun 2023   Prob (F-statistic):          1.70e-273
Time:                        21:45:05   Log-Likelihood:                 20.924
No. Observations:                 249   AIC:                            -37.85
Df Residuals:                     247   BIC:                            -30.81
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -2.6896      0.089    -30.098      0.000      -2.866      -2.514
petr4          1.3278      0.007    196.818      0.000       1.315       1.341
==============================================================================
Omnibus:                        1.350   Durbin-Watson:                   0.271
Prob(Omnibus):                  0.509   Jarque-Bera (JB):                1.052
Skew:                           0.131   Prob(JB):                        0.591
Kurtosis:                       3.180   Cond. No.                         84.1
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Uma vez estimada a regressão, vamos checar se os nossos resíduos são estacionários.

Estatística ADF: -4.1941094433497845
Valor-p: 0.0006741926650856735
Valores críticos: {'1%': -3.4569962781990573, '5%': -2.8732659015936024, '10%': -2.573018897632674}

Ao comparar as estatísticas de teste com os valores da tabela, é possível rejeitar a hipótese nula de presença de raiz unitária. Isto é, nossos resíduos são estacionários e podemos, então, passar ao passo 2 do método de Engle-Granger.

Aqui, vamos estimar o seguinte modelo de correção de erros

(1) $\begin{equation*} \Delta petr3_t = \psi_0 + \psi_1 \hat{u_{t-1}} + \psi_3 \Delta petr4_{t} + \varepsilon_t \end{equation*}$

onde $\hat{u_{t-1}}$ serão os resíduos da regressão que acabamos de estimar.

O código abaixo, por fim, estima o modelo de correção de erros.

Código

                            OLS Regression Results                            
==============================================================================
Dep. Variable:           petr3.diff()   R-squared:                       0.919
Model:                            OLS   Adj. R-squared:                  0.919
Method:                 Least Squares   F-statistic:                     1399.
Date:                Wed, 28 Jun 2023   Prob (F-statistic):          9.47e-135
Time:                        21:45:05   Log-Likelihood:                 236.27
No. Observations:                 248   AIC:                            -466.5
Df Residuals:                     245   BIC:                            -456.0
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==========================================================================================
                             coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------------
Intercept                  0.0061      0.006      1.011      0.313      -0.006       0.018
residuos_petro.shift()    -0.0985      0.027     -3.647      0.000      -0.152      -0.045
petr4.diff()               1.1090      0.021     52.797      0.000       1.068       1.150
==============================================================================
Omnibus:                        3.965   Durbin-Watson:                   2.087
Prob(Omnibus):                  0.138   Jarque-Bera (JB):                4.843
Skew:                           0.056   Prob(JB):                       0.0888
Kurtosis:                       3.675   Cond. No.                         4.58
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Observe que o coeficiente que dá a velocidade do ajustamento é residuos_petro.shift(), isto é, negativo, no valor de -0.0985 conforme vimos acima.

Ademais, mudanças na petr4.diff() têm impacto positivo sobre as mudanças da petr3.diff(), com o coeficiente de 1.1090 sendo estatisticamente significativo.

A metodologia de Johansen e o Vetor de Correção de Erros

O problema da metodologia de Engle-Granger é que ela nos dá no máximo um vetor de cointegração, independente do número de variáveis envolvidas.

Porém, se $n$ variáveis estão envolvidas no processo, então podem existir até $n-1$ vetores cointegrantes. O vetor cointegrante estimado no caso de 3 ou mais variáveis utilizando esta metodologia pode não ser único. Podendo ser uma combinação de diferentes vetores cointegrantes.

A metodologia de Johansen, por outro lado, nos diz quantos vetores cointegrantes existem entre $n$ variáveis. Uma vez determinado esse número, é possível então construir um vetor de correção de erros, que nada mais é do que uma extensão do ECM visto anteriormente.

De modo a especificar o VECM, como em Pfaff (2008), considere primeiro um Vetor Autorregressivo de ordem $p$ como

$y_t = \Pi_1 y_{t-1} + ... + \Pi_{K} y_{t-p} + \mu + \Phi D_t + \varepsilon_t \quad \text{para} \quad t = 1,...,T,$

onde $y_t$ é o vetor $(K \times 1)$ de séries no período $t$ , $\Pi_i(i = 1,...,p)$ é a matriz $(K \times K)$ de coeficientes das variáveis endógenas defasadas, $\mu$ é o vetor $(K \times 1)$ de constantes e $D_t$ é um vetor de variáveis não estocásticas, tal como dummies sazonais e de intervenção. O termo de erro $(K \times 1)$ $\varepsilon_t$ é supostamente i.i.d. tal que $\varepsilon_t \sim \mathcal{N}(0,\Sigma)$ .

Da equação acima, duas versões do VECM pode ser especificadas.

Na primeira forma, onde $y_t$ , um vetor $(Kx1)$ de séries no período $t$ entra com defasagem $t-p$ :

\begin{subequations}

(2) $\begin{align*} \Delta y_t& = \tau_1 \Delta y_{t-1} + ... + \tau_{p-1} \Delta y_{t-p+1} + \Pi y_{t-p} + \mu + \Phi D_t + \varepsilon_t \\ \tau_i& = - (I - \Pi_1 - ... - \Pi_i) \quad \text{para} \quad i = 1,...,p-1 \\ \Pi& = - (I - \Pi_1 - ... - \Pi_p) \end{align*}$

\end{subequations}

onde $\Pi_i(i=1,...,p)$ é uma matriz $(K \times K)$ de coeficientes das variáveis endógenas defasadas, $\mu$ é um vetor $(K \times 1)$ de constantes, $D_t$ é um vetor de variáveis não estocásticas, $I$ é a matriz identidade $(K \times K)$ , $\tau_i(i=1,...,p)$ é a matriz que contém os impactos cumulativos de longo prazo, dando a essa especificação o nome de forma de longo prazo.

Por fim, $\varepsilon_t$ é o vetor $(K \times 1)$ de termos de erros, supostamente i.i.d. tal que $\varepsilon_t \sim \mathcal{N}(0,\Sigma)$ .

Uma outra especificação do VECM pode ser da forma:

\begin{subequations}
\label{vecm}

(3) $\begin{align*} \Delta y_t& = \tau_1 \Delta y_{t-1} + ... + \tau_{p-1} \Delta y_{t-p+1} + \Pi y_{t-1} + \mu + \Phi D_t + \varepsilon_t \\ \tau_i& = - (\Pi_{i-1} - ... - \Pi_p) \quad \text{para} \quad i = 1,...,p-1 \\ \Pi& = - (I - \Pi_1 - ... - \Pi_p) \end{align*}$

\end{subequations}

A matriz $\Pi$ é da mesma forma da primeira especificação. Já as matrizes $\tau_i$ se diferenciam no sentido de que aqui medem efeitos transitórios, o que dá o nome dessa especificação de forma transitória.

Ademais, nessa especificação os níveis de $y_t$ entram defasadas um período apenas.

Estimando um VECM no Python

De modo a ilustrar a aplicação do VECM, vamos construir um modelo com foco na trajetória da Dívida Bruta. Para isso, devemos importar as variáveis relevantes conforme o código abaixo.

Uma vez importadas as séries, precisamos verificar se há cointegração entre elas.

Seleção do Rank de Cointegração

Utilizamos o teste de Johansen, por meio da função select_coint_rank. Em seus parâmetros, definimos as variáveis, o termo determinístico (-1 sem termo; 0 para constante; 1 para linear), o número de diferenças defasadas e o método a ser utilizado pelo teste, trace e maxeig.

O Teste vai determinar o número de vetores de cointegração ou relações de cointegração (r). O modelo VECM é utilizado quando os vetores de cointegração são maiores que 0 e menores que o número de variáveis no modelo (K).

0 < r < K; aplicar VECM

No nosso exemplo (onde K = 5), a aplicação do VECM é apropriada se o r seja o valor de 2,3 e 4, pois isso satisfaz a condição acima 0 < r < K (ou seja, 0 < r < 5).

O teste pode ser realizado usando tanto a estatística de Traço (Trace statistic) quanto a estatística do Autovalor Máximo (Maximum Eigenvalue statistic) para testar as seguintes hipóteses:

Hipótese Nula (H0): Não existe cointegração entre as variáveis (r = 0). Hipótese Alternativa (H1): Existe pelo menos uma relação de cointegração entre as variáveis (r > 0).

O teste de cointegração de Johansen avalia se a estatística de teste excede o valor crítico para rejeitar a hipótese nula e inferir a presença de cointegração entre as variáveis.

Código

Johansen cointegration test using trace test statistic with 5% significance level
=====================================
r_0 r_1 test statistic critical value
-------------------------------------
  0   5          92.10          69.82
  1   5          51.34          47.85
  2   5          22.52          29.80
-------------------------------------
Johansen cointegration test using maximum eigenvalue test statistic with 5% significance level
=====================================
r_0 r_1 test statistic critical value
-------------------------------------
  0   1          40.76          33.88
  1   2          28.82          27.59
  2   3          11.77          21.13
-------------------------------------

Cada linha da tabela resultante mostra um teste com:

Hipótese nula: “O rank de cointegração é r_0”
Hipótese alternativa:“O rank de cointegração é maior que r_0 e ≤ r_1”.

A última linha contém informações sobre o rank de cointegração a ser escolhido. Se a estatística de teste dessa linha for menor que o valor crítico correspondente, utiliza-se r_0 como o rank de cointegração. Caso contrário, utiliza-se r_1.

Essa informação é relevante para determinar o número de vetores de cointegração adequados para o modelo. Se o teste estatístico para r_0 for estatisticamente significativo, indica que o número de vetores de cointegração é pelo menos r_0. Por outro lado, se o teste para r_1 for significativo, indica que o número de vetores de cointegração é maior que r_0 e r_1.

A partir das tabelas acima, chegamos a conclusão que r_0 = 2.

Seleção da ordem de defasagem

Determinado a ordem de cointegração, determinado a ordem de defasagem. Fazemos isso por meio da função select_order. Como parâmetros, temos os dados, o máximo de defasagens e o termo determínistico.

Entre as escolhas do último, temos:

“N” - sem termos determinísticos
“co” - constante fora da relação de cointegração
“ci” - constante dentro da relação de cointegração
“lo” - tendência linear fora da relação de cointegração
“li” - tendência linear dentro da relação de cointegração

Código

{'aic': 5, 'bic': 1, 'hqic': 4, 'fpe': 4}

É sugerido a escolha de diferentes defasagens de acordo com diferentes critérios. Escolhemos o bic = 1

Estimação do VECM

Para ajustar um modelo VECM aos dados, primeiro criamos um objeto VECM no qual definimos:

Os termos determinísticos
A ordem de defasagem (lag order)
O rank de cointegração

Código

  Det. terms outside the coint. relation & lagged endog. parameters for equation dbgg   
========================================================================================
                           coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------------
L1.dbgg                  0.4057      0.199      2.041      0.041       0.016       0.795
L1.juro_real_ex_post    -0.0785      0.158     -0.498      0.619      -0.387       0.230
L1.nfsp                 -0.0113      0.256     -0.044      0.965      -0.513       0.491
L1.cambio                1.2477      0.780      1.599      0.110      -0.281       2.777
L1.dpib                 -0.2020      0.195     -1.035      0.301      -0.585       0.180
Det. terms outside the coint. relation & lagged endog. parameters for equation juro_real_ex_post
========================================================================================
                           coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------------
L1.dbgg                 -0.1318      0.126     -1.043      0.297      -0.380       0.116
L1.juro_real_ex_post     0.4766      0.100      4.756      0.000       0.280       0.673
L1.nfsp                 -0.2818      0.163     -1.729      0.084      -0.601       0.038
L1.cambio               -0.2007      0.496     -0.404      0.686      -1.173       0.772
L1.dpib                 -0.1313      0.124     -1.058      0.290      -0.375       0.112
  Det. terms outside the coint. relation & lagged endog. parameters for equation nfsp   
========================================================================================
                           coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------------
L1.dbgg                  0.1278      0.096      1.329      0.184      -0.061       0.316
L1.juro_real_ex_post     0.0412      0.076      0.540      0.589      -0.108       0.191
L1.nfsp                  0.5798      0.124      4.677      0.000       0.337       0.823
L1.cambio                1.2502      0.378      3.311      0.001       0.510       1.990
L1.dpib                  0.0218      0.094      0.231      0.817      -0.163       0.207
 Det. terms outside the coint. relation & lagged endog. parameters for equation cambio  
========================================================================================
                           coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------------
L1.dbgg                  0.0210      0.033      0.631      0.528      -0.044       0.086
L1.juro_real_ex_post    -0.0381      0.026     -1.444      0.149      -0.090       0.014
L1.nfsp                 -0.0638      0.043     -1.485      0.138      -0.148       0.020
L1.cambio                0.2907      0.131      2.222      0.026       0.034       0.547
L1.dpib                 -0.0078      0.033     -0.238      0.812      -0.072       0.056
  Det. terms outside the coint. relation & lagged endog. parameters for equation dpib   
========================================================================================
                           coef    std err          z      P>|z|      [0.025      0.975]
----------------------------------------------------------------------------------------
L1.dbgg                 -0.3222      0.136     -2.368      0.018      -0.589      -0.055
L1.juro_real_ex_post     0.0632      0.108      0.586      0.558      -0.148       0.275
L1.nfsp                  0.2577      0.175      1.470      0.142      -0.086       0.601
L1.cambio               -0.2228      0.534     -0.417      0.677      -1.270       0.824
L1.dpib                  0.5110      0.134      3.825      0.000       0.249       0.773
                Loading coefficients (alpha) for equation dbgg                
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.0081      0.034      0.239      0.811      -0.058       0.074
ec2           -0.0069      0.036     -0.194      0.846      -0.077       0.063
         Loading coefficients (alpha) for equation juro_real_ex_post          
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.0401      0.021      1.874      0.061      -0.002       0.082
ec2           -0.0414      0.023     -1.824      0.068      -0.086       0.003
                Loading coefficients (alpha) for equation nfsp                
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.0465      0.016      2.856      0.004       0.015       0.078
ec2           -0.0576      0.017     -3.340      0.001      -0.091      -0.024
               Loading coefficients (alpha) for equation cambio               
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.0021      0.006      0.380      0.704      -0.009       0.013
ec2           -0.0024      0.006     -0.400      0.689      -0.014       0.009
                Loading coefficients (alpha) for equation dpib                
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ec1            0.0461      0.023      2.001      0.045       0.001       0.091
ec2           -0.0319      0.024     -1.307      0.191      -0.080       0.016
          Cointegration relations for loading-coefficients-column 1           
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
beta.1         1.0000          0          0      0.000       1.000       1.000
beta.2     -1.128e-16          0          0      0.000   -1.13e-16   -1.13e-16
beta.3         8.3586      3.705      2.256      0.024       1.096      15.621
beta.4       -24.8637      3.500     -7.104      0.000     -31.723     -18.004
beta.5        -9.7386      6.371     -1.529      0.126     -22.225       2.748
const         39.4169      6.017      6.551      0.000      27.624      51.210
          Cointegration relations for loading-coefficients-column 2           
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
beta.1     -1.342e-17          0          0      0.000   -1.34e-17   -1.34e-17
beta.2         1.0000          0          0      0.000       1.000       1.000
beta.3        11.9639      2.365      5.058      0.000       7.328      16.600
beta.4       -18.6400      2.234     -8.344      0.000     -23.019     -14.261
beta.5        -6.7921     20.068     -0.338      0.735     -46.125      32.540
const         76.7391     18.954      4.049      0.000      39.590     113.888
==============================================================================

A representação do valores em VAR podem ser obtidos por meio da propriedade var_rep.

Código

array([[[ 1.41375584, -0.08536146, -0.02659502,  1.17626795,
         -0.23355838],
        [-0.09173148,  1.43521314, -0.44171427, -0.42627947,
         -0.24077763],
        [ 0.17429116, -0.01648485,  1.27862109,  1.16897731,
         -0.039309  ],
        [ 0.02317379, -0.04053679, -0.07447212,  1.28198379,
         -0.01242192],
        [-0.27608078,  0.03127956,  0.26103657, -0.77346052,
          1.27905325]],

       [[-0.40570265,  0.07845381,  0.0112659 , -1.24774092,
          0.20204921],
        [ 0.13182972, -0.4765953 ,  0.28178727,  0.20065519,
          0.13134929],
        [-0.12780611, -0.04116342, -0.57976932, -1.25019979,
         -0.02183696],
        [-0.02103035,  0.03814584,  0.06378313, -0.29071007,
          0.00778746],
        [ 0.32215148, -0.06318908, -0.25771294,  0.22276878,
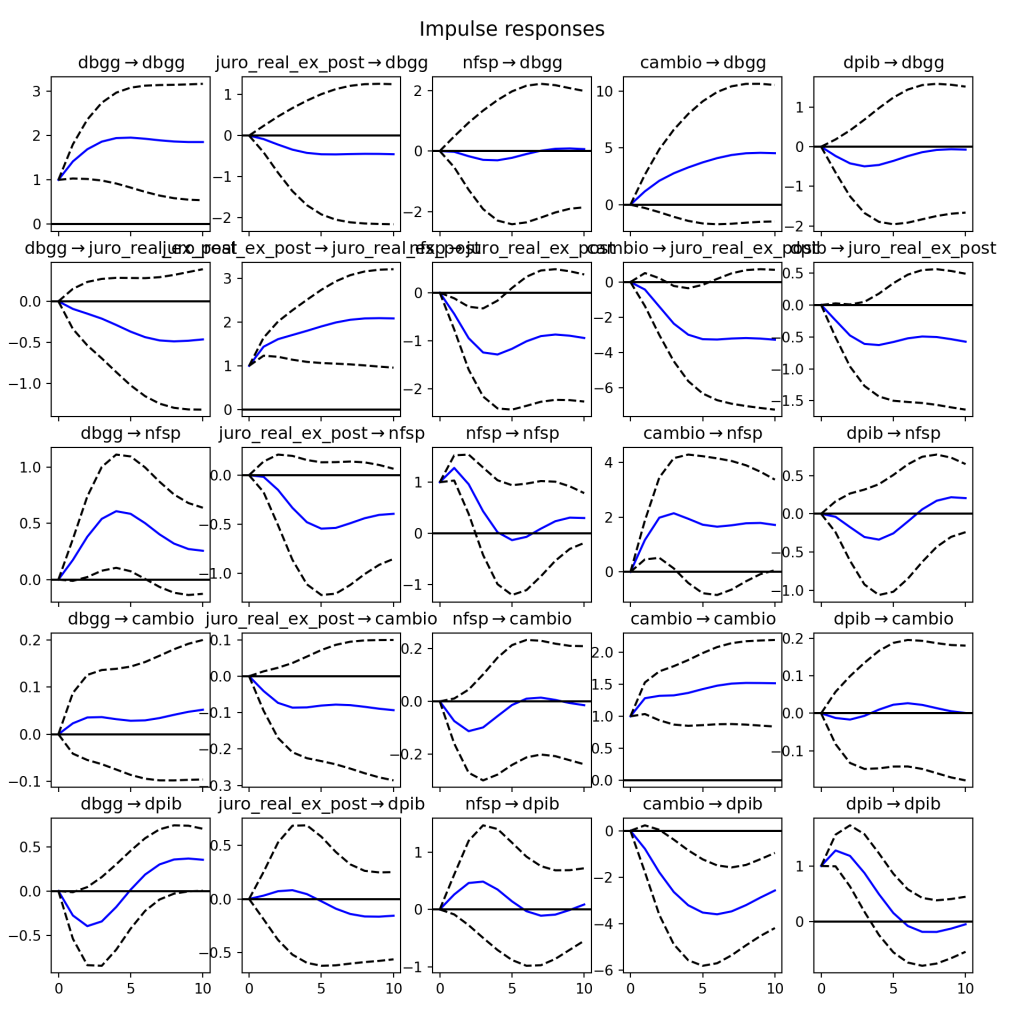
         -0.5109834 ]]])

De forma a gerar as funções de impulso-resposta, podemos aplicar o método irf.

_____________________

Quer saber mais?

Veja nossa trilha de cursos de Finanças Quantitativas

Referências

Enders, W. 2009. Applied Econometric Times Series. Wiley Series em Probability e Statistics. Wiley.

Pfaff, B. 2008. Analysis of integrated and cointegrated time series with R. Second. New York: Springer.

Verbeek, M. 2012. A Guide to Modern Econometrics. Editora Wiley.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Propensity Score com Múltiplas Variáveis no R

Análise regional da inflação com dados do IBGE usando Python

Como coletar dados do Banco Central do Chile usando a API com o Python?

Como analisar a relação de risco-retorno de ações?

Retropolando a série do desemprego no Brasil

Variáveis Instrumentais no R: qual o impacto do gasto de segurança no crime?

Outros artigos relacionados

Propensity Score com Múltiplas Variáveis no R

O escore de propensão é provavelmente a maneira mais comum de agregar múltiplas variáveis de correspondência em um único valor que pode ser correspondido, ou seja, muito útil para a realização de pareamento.

O escore de propensão é a probabilidade estimada de que uma determinada observação teria sido tratada. A correspondência de escore de propensão muitas vezes significa selecionar um conjunto de observações de controle correspondidas com valores semelhantes do escore de propensão.

Análise regional da inflação com dados do IBGE usando Python

Os dados desagregados do IPCA fornecem informações detalhadas sobre o comportamento de preços no Brasil a nível de região metropolitana e município, possibilitando ricas análises regionais de dados. Neste artigo mostramos como acessar, processar e analisar estes dados utilizando o Python.

Como coletar dados do Banco Central do Chile usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal do Banco Central do Chile através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.