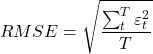Aplicações de Modelos de Volatilidade: Premissas e Previsão

Vamos verificar algumas premissas importantes sobre os modelos de volatilidade ARCH/GARCH, o funcionamento da geração de previsões dos modelos e como avaliar os resultados utilizando o R e o Python.

Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

Premissas

A volatilidade não é diretamente observável e é estimada por meio das flutuações de retorno de preços. Os retornos são iguais aos retornos médios mais os resíduos. Os resíduos são choques de retorno estocásticos dependentes do tamanho da volatilidade.

Portanto, para modelar a volatilidade, os modelos requerem premissas de distribuição dos resíduos e dos retornos médios. Quanto mais representativas dos dados reais as premissas forem, melhor o modelo criado.

Sendo assim, consideramos que

$r_t = \mu_t + a_t$

$a_t = \sigma_t \varepsilon_t \sim N(0, \sigma^2_t)$

onde $\varepsilon_t$ uma sequência de variáveis aleatórias independentes e identicamente distribuídas com média zero e variância igual 1, ou seja, um ruído branco.

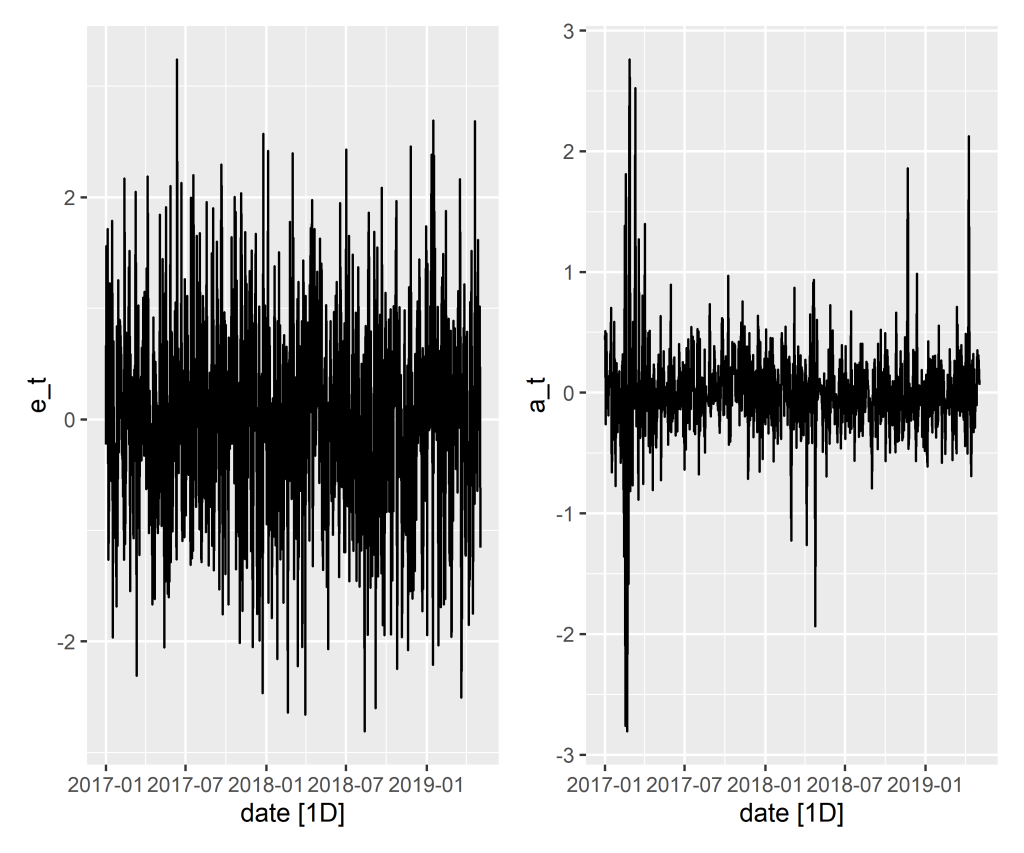
Os dois gráficos abaixo relatam o comportamento de $\varepsilon_t$ e $a_t$ , respectivamente.

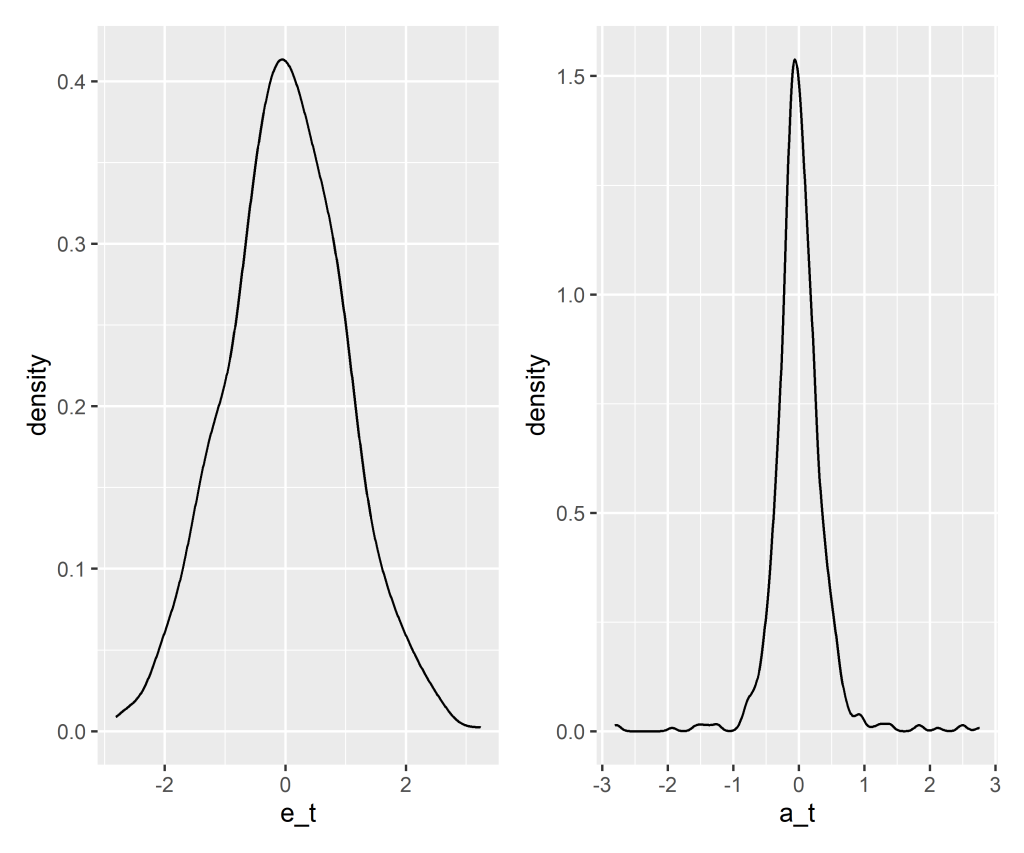
Vamos, portanto, verificar as premissas sobre o valores de $a_t$ normalizados.

$\frac{r_t - \mu_t}{\sigma_t} \sim N(0, \sigma^2_t)$

Os resíduos padronizados seguem uma distribuição, e para tornar mais realístico, devemos ter em mente:

fat tails (caudas gordas): maior probabilidade de observar altos valores de retornos (positivos ou negativos).
Skewness: assimetria da distribuição dos retornos.

Para solucionar podemos usar dois tipos de distribuições:

Distribuição t de student: permite corrigir o problema de caudas gordas, levando em consideração o valor dos graus de liberdade pelo parâmetro $\nu$ (quanto menor $\nu$ , mais gordas as caudas).
Distribuição t de student assimétrica: além de corrigir as caudas gordas, leva em consideração a assimetria (skew). Quando o valor é igual a 1, a distribuição é simétrica, menor 1 que, assimetria negativa, e maior que 1, assimetria positiva.

Quando $\nu = \infty$ e assimetria igual a 1, temos uma distribuição normal.

Quando a assimetria é igual a 1, temos uma distribuição t de student.

Modelo da Média

O valor do retorno médio pode ser considerado por diferentes formas:

Nulo
Média amostral (constante)
ARMA

Se lembrarmos que existe uma relação de risco ( $\sigma^2$ ) e retorno ( $\mu_t$ ), podemos usar o modelo da média para realizar uma leitura do comportamento da série analisada.

Interpretação do retorno médio

Retorno médio constante

$\mu_t = \mu + \lambda\sigma^2_t$

, temos que $\lambda > 0$ representa o parâmetro de risco-retorno. Isto, é o aumento no retorno esperado dado um unidade de aumento da variância (risco). (é necessário que $\lambda$ seja positivo).

AR

$\mu_t = \mu + \rho(r_{t-1} - \mu)$

, se $rho$ for positivo, prevemos que quando o retorno está acima de $\mu$ , o próximo valor também estará acima de $\mu$ e vice-versa.

se $| \rho | < 1$ significa reversão à média, isto é, os desvios de $r_t$ de $\mu$ serão transitórios.

MA

$\mu_t = \mu + \theta(r_{t-1} - \mu_{t-1})$

prevê o retorno considerando o valor o retorno passado de sua média condicional.

Performance

Ao analisar um modelo de volatilidade, devemos manter a parcimoniosidade, isto é, devemos manter o menor número possível de parâmetros estimados e preferir modelos mais simples do que complexos, se possível.

Para isso, verificamos se:

O p-value dos parâmetros são menores que 0,05 para rejeitar a hipótese nula de que o valor do parâmetro não é 0. Se for, retire-o;
Para auxiliar a validação, verificamos se o módulo da t-statistic é maior que 2;
Visualização do gráficos dos resíduos padronizados, que devem ser visualmente iguais a um ruído branco;
Não deve haver Autocorrelação dos resíduos padronizados. Podemos verificar através do gráfico FAC (ACF) ou pelo teste de Ljung-Box, que testa H0 se os dados são distribuidos independemente (o valor deve ser p > 0,05);
Para verificar se o modelo pode explicar muito bem os dados históricos por meio dos valores ajustados, utiliza-se os critérios de informação AIC e BIC, que permitem avaliar o trade-off de um modelo bem ajustado e de complexidade. Quanto menor, melhor;

Previsão

A previsão de modelos ARCH e GARCH segue os mesmos passos do modelo ARIMA. Prevê-se um passos à frente; com o resultado, realiza-se o passo seguinte e assim sucessivamente.

Para ilustrar, vemos o caso de um GARCH (1,1) que comece em $t$ :

$\hat{\sigma}_t(1) = \omega + \alpha_1 a^2_t + \beta_1 \sigma^2_1$

Para $l > 1$

$\hat{\sigma}_t(l) = \omega + (\alpha_1 + \beta_1) \hat{\sigma}_t(l - 1), \quad l > 1$

Backtesting

Backtesting é um método para avaliar a qualidade de uma previsão. Comparamos os resultados previstos pelo modelo com os dados históricos para verificar o quão próximo eles estão.

Separamos os dados históricos em duas partes:

In-sample (dentro da amostra): são usados para o ajuste.
Out-of-sample (fora da amostra): sõa reservados para o backtesting para avaliar o desempenho.

Portanto, para gerar um backtesting eficiente, temos que:

Dividir o data set em uma subamostra de estimação e previsão;
Estimar o modelo utilizando a subamostra de estimação e utilizar o modelo estimado para gerar a previsão ℎ passos à frente, onde ℎ é igual ao tamanho da subamostra de previsão;
Comparar as previsões geradas com as observações da subamostra de previsão.

Desse posse do erro de previsão, é possível calcular algumas métricas de acurácia.

A primeira consiste simplesmente na média da série de erros de previsão, isto é, o erro médio (ME), dado conforme segue:

(1) $\begin{equation*} ME = \frac{\sum_t^T{\varepsilon_t}}{T} \end{equation*}$

A segunda é a raiz quadrada do erro médio (RMSE), dada por

(2) $\begin{equation*} RMSE = \sqrt{\frac{\sum_t^T{\varepsilon_t^2}}{T}} \end{equation*}$

A terceira medida, por sua vez, é dada pela média dos erros em valores absolutos ou simplesmente erro médio absoluto (MAE), expressa conforme

(3) $\begin{equation*} MAE = \frac{\sum_t^T{|\varepsilon_t|}}{T} \end{equation*}$

Essas três medidas fazem parte do grupo de medidas que dependem da escala na qual os dados estão. Logo, elas podem ser utilizadas para efeito de comparação de diferentes modelos aplicados a mesma amostra de dados.

A quarta medida é o erro médio percentual (MPE), isto é,

(4) $\begin{equation*} MPE = \frac{\sum_t^T{p_t}}{T} \end{equation*}$

A quinta medida é o erro médio absoluto percentual (MAPE), dado conforme

(5) $\begin{equation*} MAPE = \frac{\sum_t^T{|p_t|}}{T} \end{equation*}$

Por se tratarem de percentuais, essas medidas não são sensíveis à escala dos dados.

Rolling Window

Podemos estimar e gerar previsões dos modelos de volatilidade em janelas deslizantes, isto é, utilizar janelas da amostra com o objetivo de performar repetidamente o ajuste e a previsão a medida que o tempo avança.

Há dois métodos que podemos utilizar:

Janela não fixa: o tamanho da amostra começa em um valor determinado e aumenta conforme o tempo avança.
Janela fixa: o tamanho da amostra fica fixo conforme o tempo avança, isto é, as observações passadas são removidas em detrimentos das novas.

As janelas deslizantes são muito úteis para quando desejamos avaliar o modelo e para obter os coeficientes estimados conforme o tempo, de acordo com os dados históricos de determinado período.

_____________________

Quer saber mais?

Veja nossa trilha de cursos de Finanças Quantitativas

Referências

Hyndman, R. J., e G. Athanasopoulos. 2013. Forecasting: Principles and Practice. OTexts.

MORETTIN, Pedro Alberto. Econometria financeira: um curso em séries temporais financeiras. . São Paulo: Edgard Blücher.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Resultado IPCA-15 - Novembro/2024

Resultado PNADc Trimestral - 3° Trimestre/2024

Análise exploratória para modelagem preditiva no Python

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Outros artigos relacionados

Resultado IPCA-15 - Novembro/2024

A Análise Macro apresenta os resultados do IPCA-15 de Novembro de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Resultado PNADc Trimestral - 3° Trimestre/2024

A Análise Macro apresenta os resultados da PNADc Trimestral do 3º trimestre de 2024, com gráficos elaborados em Python para coleta, tratamento e visualização de dados. Todo o conteúdo, disponível exclusivamente no Clube AM, foi desenvolvido com base nos métodos ensinados nos cursos da Análise Macro, permitindo aos assinantes acesso aos códigos e replicação das análises.

Análise exploratória para modelagem preditiva no Python

Antes de desenvolver bons modelos preditivos é necessário organizar e conhecer muito bem os dados. Neste artigo, damos algumas dicas de recursos, como gráficos, análises e estatísticas, que podem ser usados para melhorar o entendimento sobre os dados usando Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!