Modelos preditivos podem ser bastante úteis em diferentes áreas e podem ajudar a resolver diversos problemas. Os profissionais que trabalham na área, como cientistas e analistas de dados, costumam ser muito valorizados e demandados no mercado de trabalho, dado a multidisciplinaridade e complexidade das tarefas.
Para desenvolver modelos preditivos são necessários conhecimentos da área de aplicação, habilidades técnicas de programação, conhecimento de estatística, experiência em ciência de dados, dentre outros. Portanto, a operacionalização de um modelo não é nada trivial, pois são diversos os procedimentos que um profissional da área precisa sempre ter no radar. Mas se generalizarmos esses procedimentos em um fluxo de trabalho, a distância entre a idealização do modelo e sua implementação pode ser mais curta e menos árdua.
Nesse artigo apresentaremos um fluxo de trabalho que serve como um guia para desenvolver modelos preditivos, percorrendo as etapas gerais do processo que se aplicam à maioria dos casos. O objetivo desse fluxo é ter uma referência para os momentos de dúvida ou bloqueio ao desenvolver um modelo preditivo, agindo sempre como um farol para o próximo passo. No entanto, existem diversas aplicações para modelos preditivos e nem todas compartilham das mesmas características, havendo particularidades que nenhum fluxo ou guia poderia prever. Dessa forma, adaptações pontuais podem ser necessárias para casos específicos.
A seguir, descrevemos o fluxo de trabalho para modelagem preditiva e mostramos um exemplo de sua aplicação.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
1 Modelagem preditiva em 6 etapas
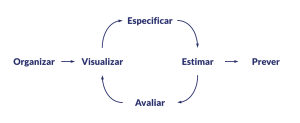
O processo de desenvolver um modelo preditivo pode ser generalizado e dividido em um fluxo composto por 6 etapas: organizar os dados; visualizar e entender os dados; especificar e definir um ou mais modelos; estimar os parâmetros ou treinar os modelos; avaliar a performance preditiva dos modelos; e, por fim, produzir previsões a partir de um modelo escolhido.
A imagem abaixo ilustra o fluxo de modelagem preditiva:
Esse é um fluxo de trabalho generalista, propício para aplicação no dia a dia de ciência de dados e, ao mesmo tempo, é recomendado por especialistas da área e em livros, como o de Hyndman e Athanasopoulos (2021).
Essas etapas formam um ciclo pois, na prática, nem sempre o processo é linear. Em muitas ocasiões é necessário retroceder ou avançar para uma etapa “vizinha”, após encontrar problemas ou fazer novas descobertas conforme a evolução do trabalho. De outra forma, se fosse um processo estritamente linear, a graça de trabalhar com modelagem preditiva seria menor.
É importante notar que esse é um fluxo prático de trabalho em ciência de dados, mas que não retrata o trabalho como um todo do profissional da área. É um guia que deve ser utilizado orientado à solução de problemas e com objetivos definidos, do contrário perde-se o propósito.
A seguir, descrevemos brevemente as etapas do fluxo de modelagem preditiva.
1.1 Organizar os dados
O primeiro passo é preparar os dados no formato correto para utilização em modelos. Esse processo pode envolver a coleta e importação de dados, a identificação de valores ausentes, filtros e outras tarefas de pré-processamento. O objetivo será, em geral, construir uma tabela de variáveis onde cada variável terá sua própria coluna, cada linha formará uma observação e os valores são armazenados nas células. Esse é o princípio de dados “tidy” e é o formato que a maioria das ferramentas para modelagem preditiva utilizam.
Vale dizer que muitos modelos têm pressupostos e requisitos diferentes, sendo que você precisará levar isso em consideração ao preparar os dados. Alguns exigem dados estacionários, outros exigem que não haja valores ausentes. Dessa forma, você precisará conhecer bem os seus dados enquanto os prepara e a análise exploratória é outra etapa que caminhará lado a lado.
1.2 Visualizar os dados
A visualização é uma etapa essencial para a compreensão dos dados. As variáveis apresentam tendência? Possuem sazonalidade? Há quebras ou observações extremas (outliers)? Observar seus dados, através de uma análise exploratória permite identificar estes padrões comuns e, posteriormente, especificar um modelo apropriado. Essa etapa pode andar em conjunto com a etapa de preparação dos dados, de modo que após entender os dados você talvez precise voltar a um passo anterior.
Existem diversas ferramentas para análise exploratória e visualização de dados. A melhor recomendação nessa etapa é: escolha uma ferramenta qualquer e foque no entendimento dos dados. Qualquer que seja a ferramenta utilizada, as perguntas (parágrafo anterior) feitas sobre os dados são as mesmas.
1.3 Especificar o modelo
Existem muitos modelos preditivos diferentes disponíveis para aplicação. Especificar um modelo apropriado para os dados é essencial para produzir previsões acuradas. Nesse sentido, além de conhecer os seus dados você precisará ter conhecimento sobre os modelos que pretende trabalhar. Papers publicados são, em geral, boas fontes para buscar esse conhecimento técnico. Ademais, grande parte dos modelos é apresentada de forma teórica e prática em Hyndman and Athanasopoulos (2021) e James et al. (2021), possuindo implementações em diversas linguagens de programação.
Em geral, a especificação de um modelo se dá por uma fórmula que representa o relacionamento entre as variáveis, por exemplo: y ~ x. As variáveis de resposta são especificadas à esquerda da fórmula e a estrutura do modelo, que pode variar, é escrita à direita. Essa representação tem apenas a finalidade de comunicar de forma clara e universal a definição de um modelo, sendo compreensível para a maioria das pessoas, mas há modelos que podem ser representados de outra forma.
1.4 Estimar o modelo
Uma vez que um modelo apropriado é definido, passamos à estimação ou treinamento do modelo com os dados. Isso significa que algum método estatístico, econométrico ou técnica de aprendizado de máquina será empregado aos dados para obtenção de estimativas que podem ser usadas para prever novos dados. É nessa etapa em que o conhecimento de matemática e a estatística podem fazer diferença, apesar de existirem ferramentas automatizadas ou soluções “caixa preta” para uso.
Em geral, existem implementações para a maioria dos modelos nas principais linguagens de programação, eliminando o trabalho de escrever um extenso código fonte. Em grande parte dos casos, basta importar um pacote e usar uma função que estima o modelo para uma determinada entrada de dados.
1.5 Avaliar a performance
Após termos um modelo estimado, é importante verificar o desempenho dele sobre dados que ele ainda não conhece, se o objetivo for previsão acurada. Existem várias ferramentas de diagnóstico disponíveis para verificar o ajuste do modelo, assim como medidas de acurácia que permitem comparar um modelo com outro: em problemas de regressão, o MSE é a métrica mais comumente utilizada; já em problemas de classificação, a taxa de erro é a métrica mais comumente utilizada.
Conforme a avaliação do modelo, é possível que sejam necessárias readequações para cumprir um objetivo, seja na especificação ou até mesmo nos dados utilizados. Em outras palavras, o fluxo de trabalho não é simplesmente um amontoado de procedimentos a serem implementados sequencialmente, mas sim um processo de descobrimento que envolve, na vida real, sucessivas tentativas e erros.
Além disso, há técnicas como a validação cruzada que auxiliam na tomada de decisão entre mais de um modelo. É sempre preferível ter mais de um modelo “candidato” potencialmente usado para modelagem preditiva, além de modelos básicos para simples comparação.
1.6 Produzir previsões
Com um modelo especificado, estimado e diagnosticado, é hora de produzir as previsões fora da amostra. Para alguns modelos é possível simplesmente chamar uma função especificando o número de novas previsões desejadas (modelos temporais univariados); para outros será necessário prover uma tabela com novos valores das variáveis regressoras utilizadas no modelo (modelos multivariados), que servirá para produzir as previsões da variável de interesse.
2 Exemplo prático com dados macroeconômicos
Agora vamos apresentar um exemplo do fluxo de trabalho para modelagem preditiva, percorrendo cada etapa do processo. Faremos um exercício didático e simples, apenas para introduzir a prática desse processo, mas utilizaremos dados e uma problemática real.
Por conveniência, abordaremos um problema de previsão para séries temporais, usando como variável resposta o PIB do Brasil, cuja previsibilidade é de grande interesse para diversos atores da sociedade. Os dados utilizados estão em frequência trimestral, taxa de crescimento acumulada em quatro trimestres, e a fonte é o IBGE.
2.1 Organizar os dados
Primeiro coletamos os dados online e preparamos a série temporal do PIB em formato propício para o exercício:
R
Código
| data | pib |
|---|---|
| 2021 Q4 | 5.0 |
| 2022 Q1 | 5.2 |
| 2022 Q2 | 3.2 |
| 2022 Q3 | 3.0 |
| 2022 Q4 | 2.9 |
| 2023 Q1 | 3.3 |
Python
Código
pib
data
2022-01-01 00:00:00+00:00 5.2
2022-04-01 00:00:00+00:00 3.2
2022-07-01 00:00:00+00:00 3.0
2022-10-01 00:00:00+00:00 2.9
2023-01-01 00:00:00+00:00 3.32.2 Visualizar os dados
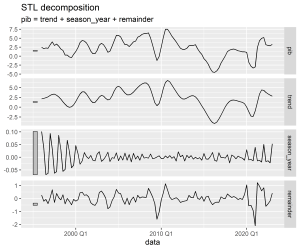
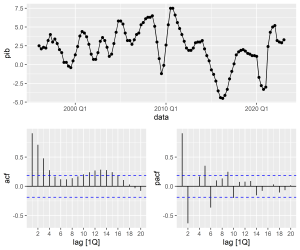
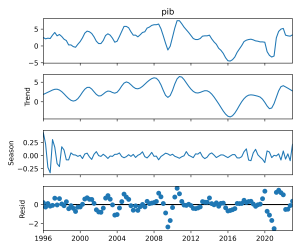
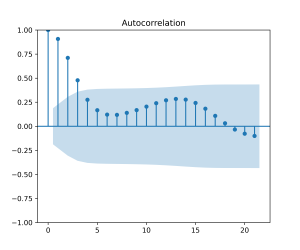
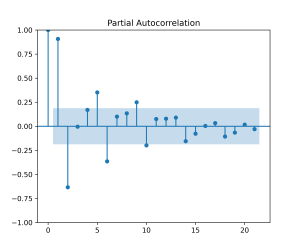
Em seguida, realizamos uma breve análise exploratória de dados, focando na decomposição da série temporal e na análise de autocorrelação:
R
Python
Código
Código
Código
2.3 Especificar o modelo
Neste exercício de modelagem preditiva estamos utilizando somente os dados do PIB, ou seja, uma única série temporal. Por um lado, isso limita bastante o escopo de modelos que poderíamos utilizar, por outro lado, mantemos o exercício simples e compreensível.
Dentro das possibilidades de modelagem preditiva, aplicáveis neste exercício, destacam-se os modelos tradicionais de séries temporais conhecidos como ARIMA, abreviação de Autoregressive integrated moving average, que exploram os valores defasados da própria série para produzir previsões para o futuro. A especificação geral destes modelos pode ser representada como abaixo:
Os gráficos da FAC e da FACP indicam que os modelos MA(4) e AR(2) podem ser candidatos para previsão do PIB. Vamos especificar estes modelos simples e um modelo automatizado, o chamado Auto ARIMA, onde a especificação é feita por algoritmo minimizando critérios de informação.
2.4 Estimar o modelo
Identificado um (ou mais) modelo apropriado, podemos prosseguir com a estimação. Existem diversas ferramentas open source para tal, com diferenças mínimas e performances semelhantes. Abaixo realizamos a estimativa dos modelos e reportamos os principais resultados:
R
Código
| .model | term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| ar2 | ar1 | 1.4799896 | 0.0722740 | 20.477477 | 0.0000000 |
| ar2 | ar2 | -0.6326004 | 0.0720644 | -8.778264 | 0.0000000 |
| ar2 | constant | 0.3456632 | 0.0786924 | 4.392588 | 0.0000261 |
| ma4 | ma1 | 1.6917696 | 0.0792438 | 21.348922 | 0.0000000 |
| ma4 | ma2 | 1.7116763 | 0.1062076 | 16.116329 | 0.0000000 |
| ma4 | ma3 | 1.6859319 | 0.0931244 | 18.104077 | 0.0000000 |
| ma4 | ma4 | 0.6810574 | 0.0772698 | 8.814019 | 0.0000000 |
| ma4 | constant | 2.2559324 | 0.3938682 | 5.727633 | 0.0000001 |
| auto_arima | ar1 | 0.8102240 | 0.0904910 | 8.953641 | 0.0000000 |
| auto_arima | ar2 | 0.6761718 | 0.1273448 | 5.309771 | 0.0000006 |
| auto_arima | ar3 | -0.5487289 | 0.0944244 | -5.811306 | 0.0000001 |
| auto_arima | ma1 | 0.9847107 | 0.0538383 | 18.290139 | 0.0000000 |
| auto_arima | sar1 | -0.8944039 | 0.1000853 | -8.936417 | 0.0000000 |
| auto_arima | sar2 | -0.4560781 | 0.1177493 | -3.873297 | 0.0001836 |
| auto_arima | constant | 0.3372485 | 0.1065431 | 3.165372 | 0.0020083 |
Python
Código
Código
| Dep. Variable: | y | No. Observations: | 109 |
| Model: | SARIMAX(1, 0, 0) | Log Likelihood | -164.504 |
| Date: | sex, 21 jul 2023 | AIC | 335.008 |
| Time: | 12:06:35 | BIC | 343.082 |
| Sample: | 01-01-1996 | HQIC | 338.282 |
| - 01-01-2023 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
| intercept | 0.2293 | 0.128 | 1.797 | 0.072 | -0.021 | 0.479 |
| ar.L1 | 0.9010 | 0.039 | 22.921 | 0.000 | 0.824 | 0.978 |
| sigma2 | 1.1796 | 0.119 | 9.890 | 0.000 | 0.946 | 1.413 |
| Ljung-Box (L1) (Q): | 38.45 | Jarque-Bera (JB): | 55.17 |
| Prob(Q): | 0.00 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 2.27 | Skew: | 0.81 |
| Prob(H) (two-sided): | 0.02 | Kurtosis: | 6.09 |
Código
| Dep. Variable: | y | No. Observations: | 109 |
| Model: | SARIMAX(0, 0, 4) | Log Likelihood | -108.193 |
| Date: | sex, 21 jul 2023 | AIC | 228.385 |
| Time: | 12:06:35 | BIC | 244.534 |
| Sample: | 01-01-1996 | HQIC | 234.934 |
| - 01-01-2023 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
| intercept | 2.2516 | 0.449 | 5.013 | 0.000 | 1.371 | 3.132 |
| ma.L1 | 1.7011 | 6.691 | 0.254 | 0.799 | -11.413 | 14.815 |
| ma.L2 | 1.7137 | 6.038 | 0.284 | 0.777 | -10.121 | 13.549 |
| ma.L3 | 1.6932 | 9.162 | 0.185 | 0.853 | -16.263 | 19.650 |
| ma.L4 | 0.6806 | 5.284 | 0.129 | 0.898 | -9.677 | 11.038 |
| sigma2 | 0.3765 | 2.932 | 0.128 | 0.898 | -5.370 | 6.123 |
| Ljung-Box (L1) (Q): | 2.77 | Jarque-Bera (JB): | 41.19 |
| Prob(Q): | 0.10 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 3.02 | Skew: | -0.30 |
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 5.95 |
Código
| Dep. Variable: | y | No. Observations: | 109 |
| Model: | SARIMAX(2, 0, 0)x(2, 0, [1], 4) | Log Likelihood | -93.443 |
| Date: | sex, 21 jul 2023 | AIC | 200.885 |
| Time: | 12:06:35 | BIC | 219.725 |
| Sample: | 01-01-1996 | HQIC | 208.525 |
| - 01-01-2023 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
| intercept | 0.0175 | 0.040 | 0.435 | 0.664 | -0.061 | 0.096 |
| ar.L1 | 1.8145 | 0.057 | 31.760 | 0.000 | 1.703 | 1.926 |
| ar.L2 | -0.8190 | 0.057 | -14.333 | 0.000 | -0.931 | -0.707 |
| ar.S.L4 | -0.4637 | 0.118 | -3.914 | 0.000 | -0.696 | -0.232 |
| ar.S.L8 | -0.2170 | 0.159 | -1.361 | 0.173 | -0.529 | 0.095 |
| ma.S.L4 | -0.9601 | 0.226 | -4.254 | 0.000 | -1.402 | -0.518 |
| sigma2 | 0.2802 | 0.043 | 6.491 | 0.000 | 0.196 | 0.365 |
| Ljung-Box (L1) (Q): | 0.12 | Jarque-Bera (JB): | 132.62 |
| Prob(Q): | 0.73 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 2.12 | Skew: | -0.92 |
| Prob(H) (two-sided): | 0.03 | Kurtosis: | 8.08 |
Note que decidimos não separar amostras, nem implementar uma validação cruzada, com finalidade de testar os modelos com dados desconhecidos. Esse seria um exercício interessante e recomendável, mas deixamos como sugestão para o leitor.
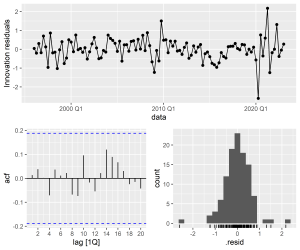
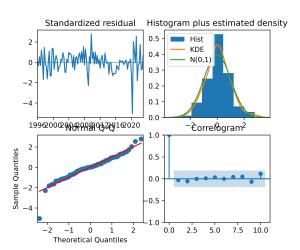
2.5 Avaliar a performance
Para avaliar esses tipos de modelos podemos usar critérios de informação, análise de resíduos, métricas de acurácia, testes de autocorrelação, etc.. Aqui nos limitaremos a reportar as duas primeiras:
R
Código
| .model | sigma2 | log_lik | AIC | AICc | BIC | ar_roots | ma_roots |
|---|---|---|---|---|---|---|---|
| auto_arima | 0.3690189 | -101.1818 | 218.3636 | 219.8036 | 239.8944 | 0.5986465+0.9265426i, -0.9265426+0.5986465i, -0.5986465-0.9265426i, 0.9265426-0.5986465i, 0.9265426+0.5986465i, -1.2156227+0.0000000i, 1.2239369+0.0335031i, -0.5986465+0.9265426i, -0.9265426-0.5986465i, 0.5986465-0.9265426i, 1.2239369-0.0335031i | -1.015527+0i |
| ma4 | 0.3999566 | -108.1208 | 228.2417 | 229.0652 | 244.3898 | -0.0091484+0.9999588i, -1.0258211-0.0000000i, -0.0091484-0.9999588i, -1.4313443+0.0000000i | |
| ar2 | 0.7116138 | -135.9748 | 279.9496 | 280.3342 | 290.7150 | 1.169766+0.460894i, 1.169766-0.460894i |
Código
Python
Código
aic aicc bic
auto_arima 200.885366 201.994276 219.724801
ma4 228.385418 229.208947 244.533505
ar1 335.007581 335.236152 343.081624Código
2.6 Produzir previsões
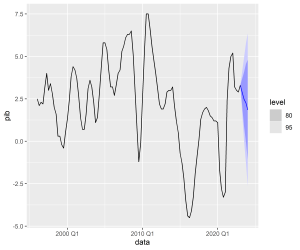
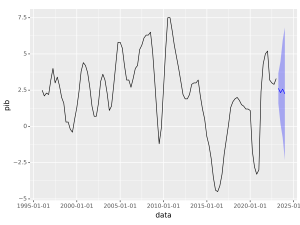
Por fim, produzimos as previsões fora da amostra (para o futuro) a partir do modelo escolhido:
R
Código
| .model | data | pib | .mean |
|---|---|---|---|
| auto_arima | 2023 Q2 | N(2.9, 0.37) | 2.896980 |
| auto_arima | 2023 Q3 | N(2.5, 1.6) | 2.477543 |
| auto_arima | 2023 Q4 | N(2.3, 3.2) | 2.255566 |
| auto_arima | 2024 Q1 | N(1.8, 5.3) | 1.845606 |
Código
Python
Código
(2023-04-01 00:00:00+00:00 2.628136
2023-07-01 00:00:00+00:00 2.326481
2023-10-01 00:00:00+00:00 2.572363
2024-01-01 00:00:00+00:00 2.246746
Freq: QS-JAN, dtype: float64, array([[ 1.58635348, 3.66991844],
[ 0.1701481 , 4.48281431],
[-0.78258681, 5.92731292],
[-2.33142665, 6.82491794]]))Código
3 Conclusão
Neste artigo, apresentamos um guia de trabalho para desenvolver modelos preditivos, percorrendo as principais etapas para se ter uma visão geral do processo. Mostramos um exemplo prático de ponta a ponta, usando as linguagens de programação R e Python.
4 Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
5 Referências
Hyndman, R. J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3. Accessed on 2023-07-13.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2021). An introduction to statistical learning. New York: Springer.