O Banco Central deve reagir a um choque de preços administrados?

Neste exercício, mostramos como identificar um choque dos preços administrados sobre os preços livres utilizando um Vetor Autoregressivo e Função de Impulso Resposta. Realizamos a coleta, tratamento, visualização e criação do modelo usando o Python.

Introdução

Alguns economistas brasileiros costumam fazer uso do termo inflação de custos (em contradição à inflação de demanda) para justificar o fato de que não faria sentido utilizar um instrumento que atua sobre a demanda, os juros, para conter um choque de oferta.

Mostramos nesse exercício que na ocorrência de um choque nos chamados preços administrados, seria um equívoco o Banco Central não reagir aos efeitos secundários do mesmo, isto é, efeitos sobre outros preços. A leniência com choques de oferta tem como efeito o desvio da inflação efetiva em relação à meta e consequente elevação das expectativas dos agentes privados, arranhando assim a credibilidade da autoridade monetária.

Preços livres vs. preços administrados

Para ilustrar o argumento, vamos dividir a inflação medida pelo IPCA da forma que segue

$\pi_t = \alpha_1 \pi_t^{livres} + \alpha_2 \pi_t^{admin}$

isto é, a inflação medida pelo IPCA passa a ser uma combinação linear entre a inflação de preços livres e a inflação de preços administrados (Preços administrados são aqueles estabelecidos por contrato, por órgão público ou agência reguladora e, geralmente, são menos sensíveis às condições de mercado)

Atualmente, são considerados preços administrados, 22 subitens e 1 item do IPCA. Para maiores detalhes sobre esses preços, ver o Texto para Discussão 305 do Banco Central, titulado Preços Administrados: projeção e repasse cambial.

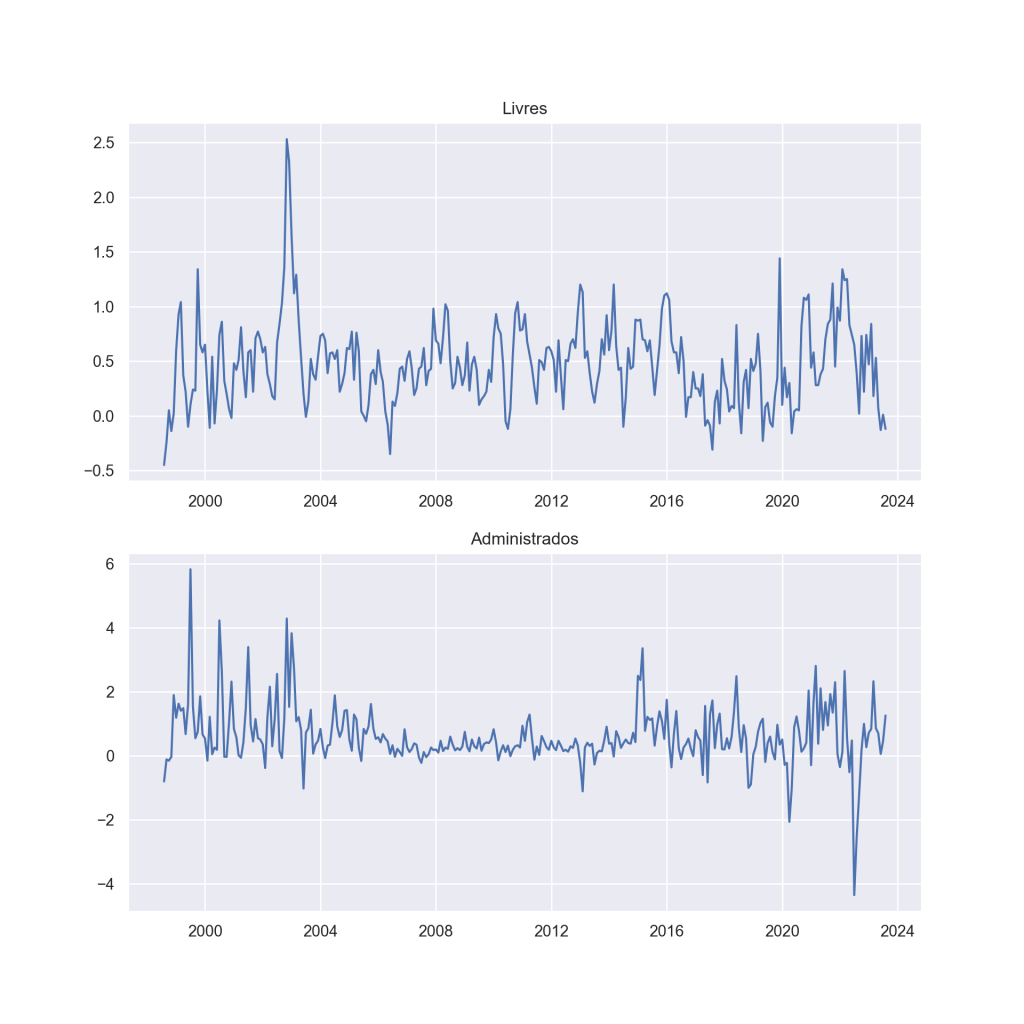
Sabemos, entretanto, que os preços livres e os preços administrados não são independentes, uma vez que muitos dos bens considerados administrados servem de insumo para os bens livres - pense, por exemplo, na energia elétrica. Coletamos, portanto, a inflação mensal geral, dos preços livres e administrados diretamente do Banco Central.

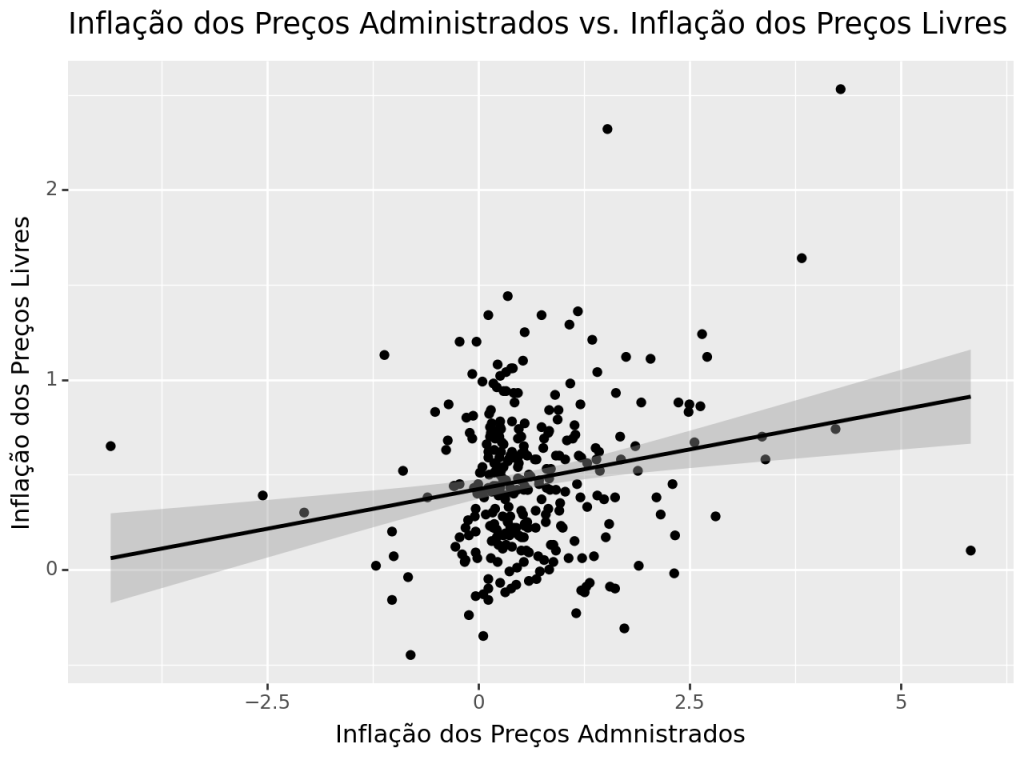
Através de uma regressão linear simples e de um gráfico de dispersão, verificamos a relação entre as duas variáveis, como segue:

Código

OLS Regression Results
Dep. Variable:	ipca	R-squared (uncentered):	0.997
Model:	OLS	Adj. R-squared (uncentered):	0.997
Method:	Least Squares	F-statistic:	5.324e+04
Date:	Fri, 15 Sep 2023	Prob (F-statistic):	0.00
Time:	17:35:06	Log-Likelihood:	587.37
No. Observations:	301	AIC:	-1171.
Df Residuals:	299	BIC:	-1163.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Livres	0.7487	0.004	195.690	0.000	0.741	0.756
Administrados	0.2471	0.002	117.000	0.000	0.243	0.251

Omnibus:	427.098	Durbin-Watson:	1.310
Prob(Omnibus):	0.000	Jarque-Bera (JB):	77286.326
Skew:	-6.685	Prob(JB):	0.00
Kurtosis:	80.354	Cond. No.	2.37

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Estimando um VAR

Um VAR irá descrever a evolução dinâmica de um determinado número de variáveis de acordo com a história comum entre elas. Para ilustrar, considere um vetor autorregressivo de ordem 1, como

$Y_{t} = \delta_{1} + \theta_{11} Y_{t-1} + \theta_{12} X_{t-1} + \epsilon_{1t} \\ X_{t} = \delta_{2} + \theta_{21} Y_{t-1} + \theta_{22} X_{t-1} + \epsilon_{2t}$

onde $\epsilon_{1t}$ e $\epsilon_{2t}$ são ruídos brancos independentes das estórias de $Y$ e $X$ , mas que podem estar correlacionados. Se, por exemplo, $\theta_{12} \neq 0$ , significa dizer que a estória de $X$ ajuda a explicar $Y$ . O sistema acima, a propósito, pode ser representando da seguinte forma, como faz Tsay (2008) :

$z_{t} = \phi_{0} + \phi_{1} z_{t-1} + \alpha_{t}$

Ou, ainda, como

$\begin{bmatrix} z_{1t} \\ z_{2t} \end{bmatrix} = \begin{bmatrix} \phi_{10} \\ \phi_{20} \end{bmatrix} + \begin{bmatrix} \phi_{1,11} & \phi_{1,12} \\ \phi_{1,21} & \phi_{1,22} \end{bmatrix} \begin{bmatrix} z_{1, t-1} \\ z_{2, t-1} \end{bmatrix} + \begin{bmatrix} \alpha_{1t} \\ \alpha_{2t} \end{bmatrix}$

Esse sistema de ordem 1, a propósito, pode ser generalizado para qualquer ordem $p$ como

$z_{t} = \phi_{0} + \sum_{i=1}^{p} \phi_{i} z_{t-i} + \alpha_{t}$

{#eq-varp}

onde $z_{t}$ para $t = 1,...,T$ é uma vetor $M x 1$ contendo observações de $M$ séries temporais, $\phi_{0}$ é um vetor $M x 1$ de interceptos, $\phi_{i}$ é uma matriz $M x M$ de coeficientes e $\alpha_{t}$ é um vetor $M x 1$ de erros, independentes e identicamente distribuídos, com média zero e covariância igual a $\Sigma_{\alpha}$ .

É conveniente representar @varp com a utilização do operador defasagem $\phi (L) = I_{k} - \phi_{1} L - ... - \phi_{p} L^{p}$ como

$\phi (L) z_{t} = \phi_{0} + \alpha_{t}$

Supondo que as séries em destaque sejam estacionárias, podemos estimar um VAR entre elas.

Para isso, devemos primeiro definir a ordem de defasagem. Isso é feito abaixo.

Código

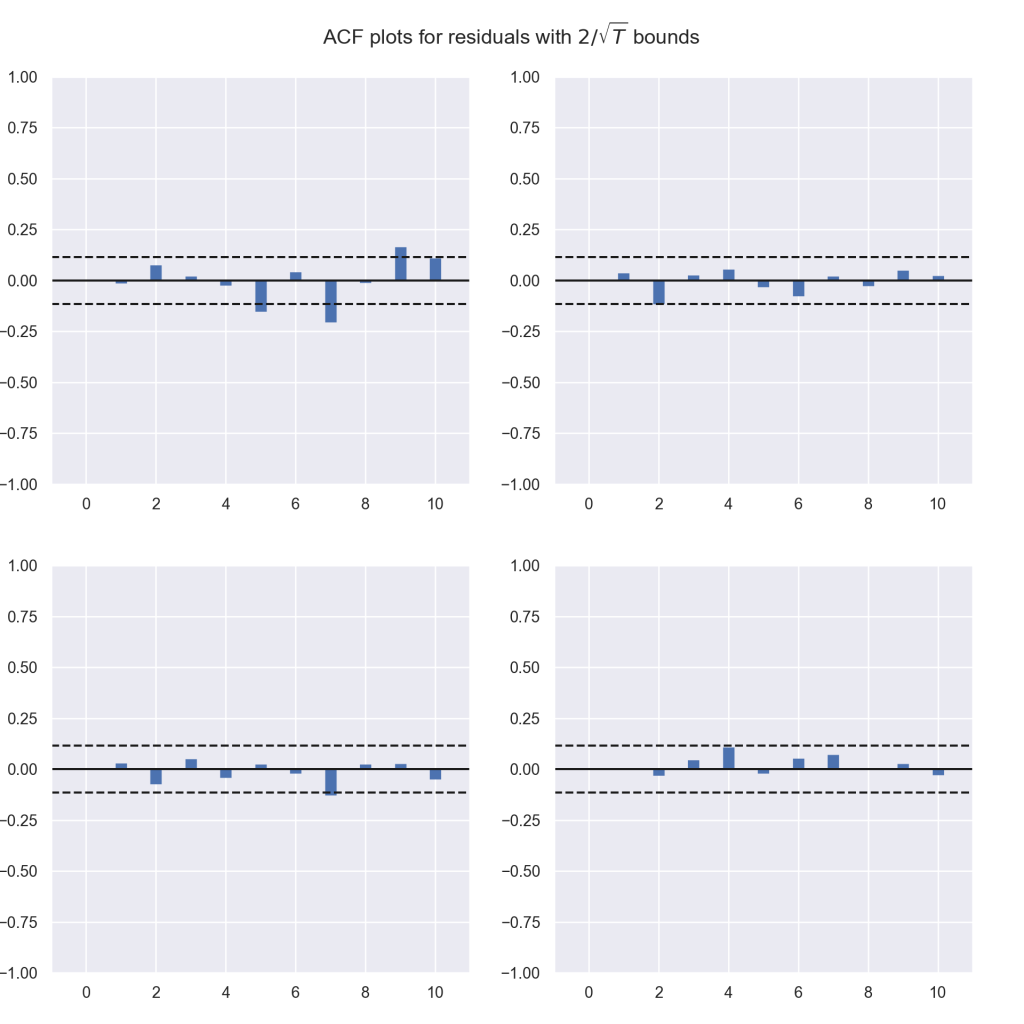
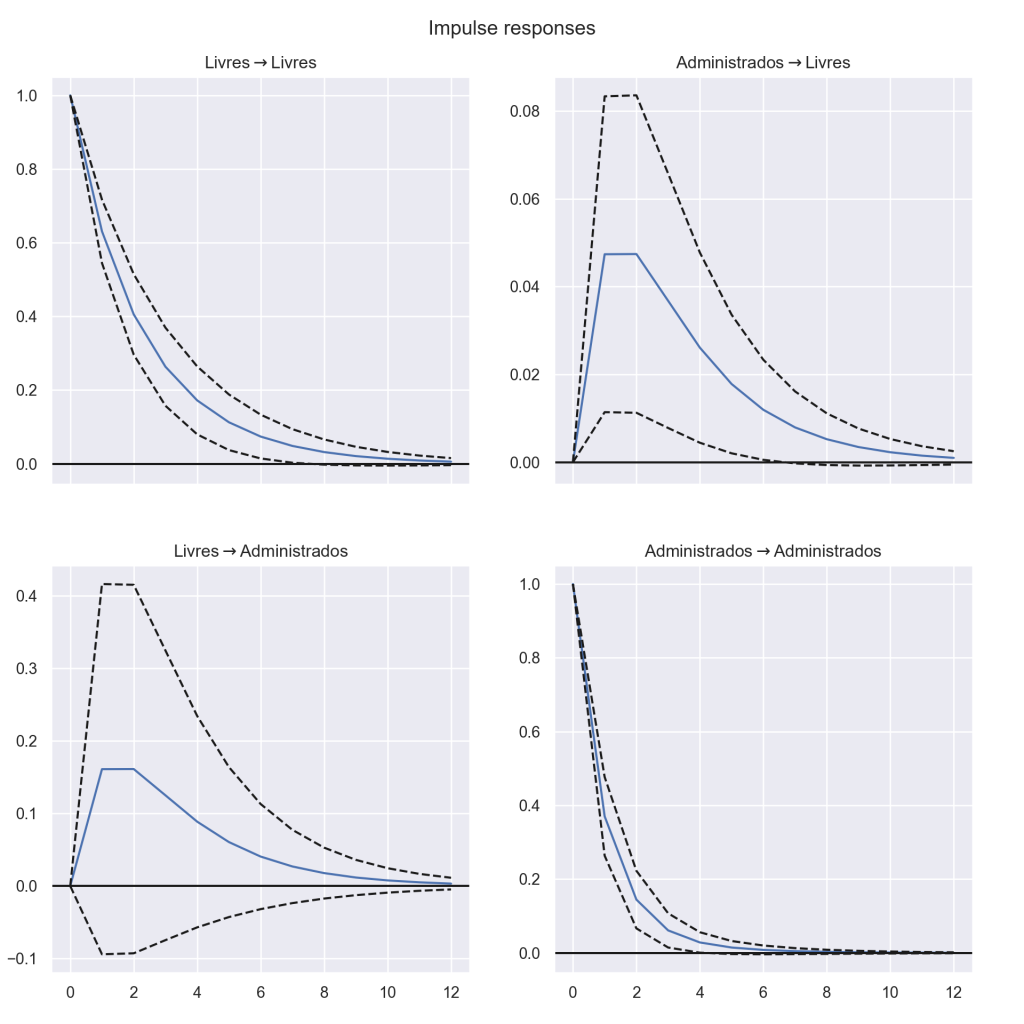
{'aic': 1, 'bic': 1, 'hqic': 1, 'fpe': 1} Pelo resultado, vemos que a melhor seleção será um VAR(1). Após estimar o VAR, verificamos a autocorrelação dos resíduos. Por fim, verificamos o choque das variáveis, conforme uma função impulso resposta. O resultado é visto abaixo:

Pelo gráfico acima, verificamos que há um efeito positivo de um choque do IPCA Administrado sobre o IPCA livres.

Quer aprender mais?

- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;

- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;

- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Como tratar dados no Python? Parte 1: selecionando colunas

Como lidar com erros de coleta de dados? Exemplo prático com dados do Banco Central

Como sumarizar divulgações trimestrais de empresas usando IA no Python

Como usar IA para sumarizar dados de demonstrações de empresas brasileiras no Python

O que é Inteligência Artificial Generativa e como usar para negócios?

Análise de impacto fiscal sobre o dolár com Python

Outros artigos relacionados

Como tratar dados no Python? Parte 1: selecionando colunas

Como extrair somente as colunas que interessam em uma tabela de dados usando Python? Neste tutorial mostramos os métodos de selecionar colunas disponíveis na biblioteca pandas, que tem como vantagem sua sintaxe simples e prática.

Como lidar com erros de coleta de dados? Exemplo prático com dados do Banco Central

A coleta de dados é uma etapa bastante suscetível a erros, presente em toda análise de dados ou modelo preditivo. Devido a isso e sua importância, muitas pessoas ficam “travadas” quando aparece uma mensagem de erro. Neste exercício mostramos como resolver esse problema usando programação.

Como sumarizar divulgações trimestrais de empresas usando IA no Python

Neste exercício, iremos utilizar a inteligência artificial no Python para analisar e sumarizar divulgações trimestrais de empresas. Focaremos no uso de ferramentas como Gemini e técnicas de processamento de linguagem natural para extrair informações de documentos PDF relacionados aos relatórios financeiros das empresas.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!