A ideia básica contida em uma Support Vector Machine (SVM) é a de separar conjuntos de objetos que pertençam a diferentes classes. A figura abaixo ilustra.
A definição do hiperplano que dividirá as diferentes classes passa por um algoritmo de aprendizado supervisionado. Esse plano delimitado dividirá o espaço criando partições homogêneas de cada lado.1
SVMs podem ser adaptados para uso em qualquer tipo de tarefa de aprendizado, incluindo problemas de classificação e também de previsão numérica. A seguir, algumas clássicas aplicações:
- Identificação de doenças genéticas;
- Categorização de textos, como identificação da linguagem utilizada;
- Identificação de falhas em motores à combustão, falhas de segurança ou terremotos.
SVMs são mais facilmente entendidos quando utilizados para classificações binárias, onde o método tem sido tradicionalmente aplicado.
O nome Support Vector Machine, diga-se, é uma generalização de um classificador simples denominado maximal margin classifier, que separa as classes do conjunto com base em uma fronteira linear. Uma primeira extensão desse classificador simples é o support vector classifier, que pode ser aplicado a um leque maior de casos. Nesse contexto, o SVM é uma extensão desse último, de modo a acomodar fronteiras não-lineares.
Para aprender mais e ter acesso a códigos confira o curso de Modelagem e Previsão usando Python ou comece do zero em análise de dados com a formação Do Zero à Análise de Dados com Python.
O que é um hiperplano?
Em um espaço de dimensão , um hiperplano é um subespaço afinado plano de dimensão
.2 Isso dito, em duas dimensões, um hiperplano será uma linha, já em três dimensões será um plano. Em duas dimensões, um hiperplano pode ser definido como:
Para dimensões, basta fazermos
Assim, quando não satisfaz Equação 1, ou
Ou então,
De modo que podemos pensar no hiperplano dividindo o espaço de dimensão em duas metades.
Classificação usando um hiperplano
Suponha agora que nós temos um matriz
de dados que consiste em
observações de treino no espaço
,
de modo que essas observações caem em duas classes, isto é,
, onde
representa uma classe e
representa a outra.
Nós também temos uma observação de teste, um vetor de variáveis observadas
.
Nosso objetivo será o de desenvolver um classificador baseado nos dados de treino que irá classificar corretamente as observações de teste usando as características de medição.
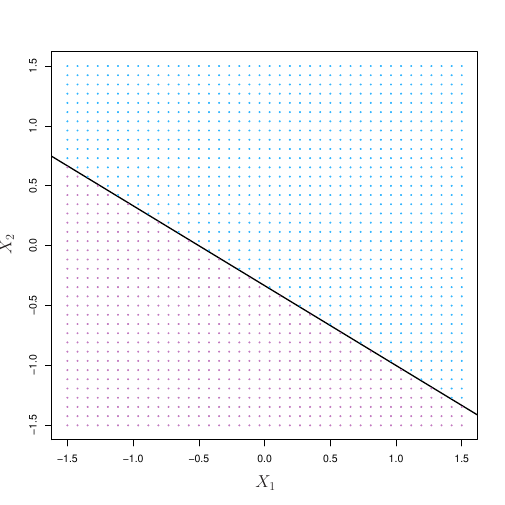
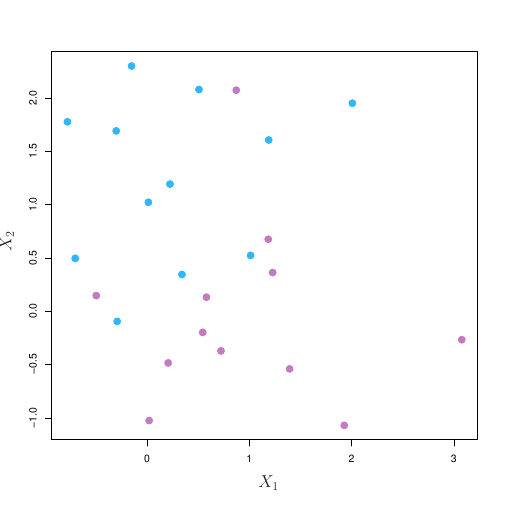
Suponha então que seja possível construir um hiperplano que separe as observações de treino de acordo com os labels de suas classes.
Usando um hiperplano para classificação
Podemos nomear as observações azuis como sendo e as roxas como
. Assim, o hiperplano irá aplicar
se
e
se
.
Assim, a observação de teste é alocada a uma classe a depender de qual lado esteja do hiperplano.3
Maximal Margin Classifier
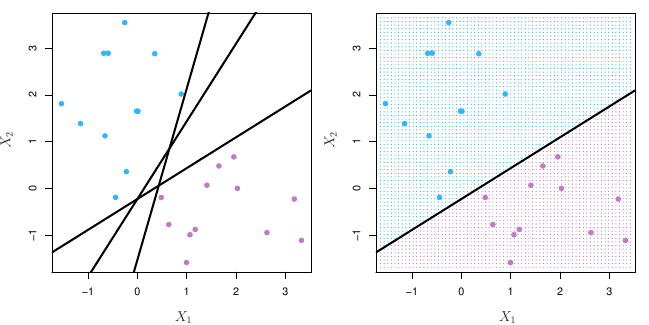
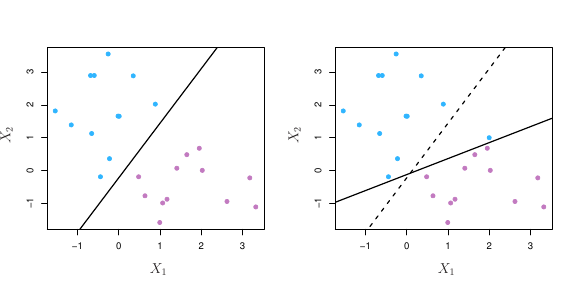
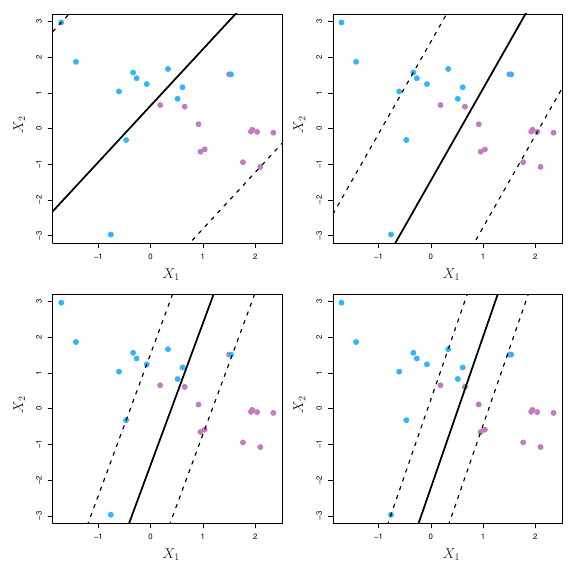
De forma geral, se nossos dados podem ser separados de forma perfeita usando um hiperplano, existirá um número infinito de possibilidades. Na figura 3, por exemplo, vimos três possibilidades de hiperplanos. Precisamos então escolher qual deles iremos utilizar para separar nossas observações.
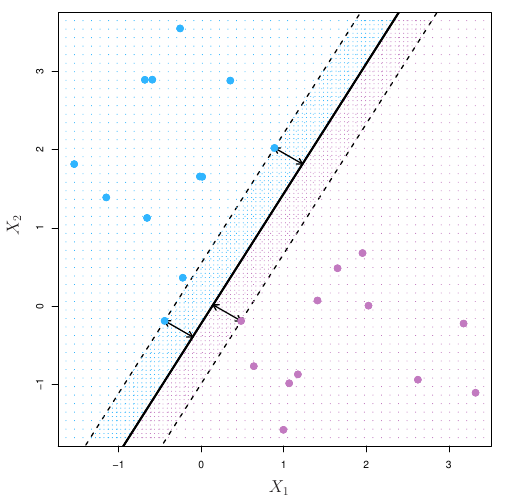
Podemos usar para isso o classificador de margem máxima. Observe, por exemplo, a figura abaixo:
Há novamente duas classes de observações, mostradas em azul e roxo. O hiperplano de margem máxima é mostrado como sendo uma linha sólida. A margem será então a distância da linha sólida até as linhas tracejadas. As linhas azuis e roxas que se encontram nas linhas tracejadas são os vetores de suporte e a distância desses pontos até o hiperplano é indicado pelas flechas. Por fim, as grades roxas e azuis indicam a regra de decisão feita por um classificador baseado no hiperplano de separação.
Em termos mais formais, considere um conjunto de observações de treino e as classes
. O hiperplano de margem máxima será então a solução para o problema de otimização dado por
De modo que as restrições garantem que cada observação estará no lado correto do hiperplano e ao menos à distância M do hiperplano. representa assim a margem do nosso hiperplano e o problema de otimização escolhe
de modo a maximizar
.
Support Vector Classifiers
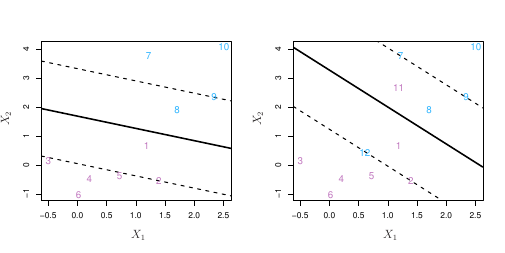
O fato do hiperplano de margem máxima ser extremamente sensível a mudanças em uma única observação sugere que estamos incorrendo em problema de overfit.
Nesse caso, nós podemos considerar um classificador baseado em hiperplano que não separe de forma perfeita as duas classes, de modo a
- Aumentar a robustez a observações individuais
- Melhor classificar da maioria das observações de treino
Assim, nós permitimos que algumas observações estejam colocadas no lado errado do hiperplano.
O problema passa a ser colocado nos seguintes termos
onde é um parâmetro de sintonia não-negativo.
A solução do problema nos dará o nosso classificador. Ele irá classificar uma observação de teste a depender de qual lado do hiperplano ela estará. O hiperplano é escolhido de modo a separar a maioria das observações de treino em duas classes, mas pode classificar de forma errada algumas das observações.
As variáveis de folga é que irão permitir que as observações individuais estejam do lado errado da margem ou do hiperplano. Se
, a observação
estará no lado correto da margem. Se
, ela estará no lado errado da margem. Por fim, se
, ela estará do lado errado do hiperplano.
O parâmetro , nesse contexto, é quem dará o controle sobre o quanto nós toleramos que as observações violem a margem e o hiperplano. Se
, nós não toleramos violação. Maiores valores para
implicam em maior tolerância na violação.
Support Vector Machine
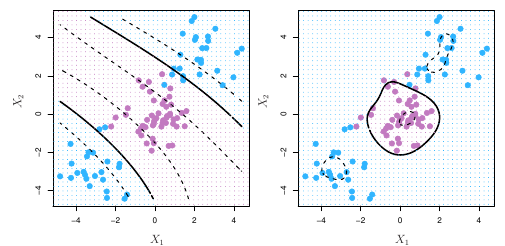
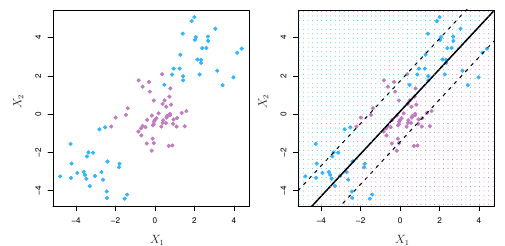
O support vector classifier é uma abordagem natural para classificação se a fronteira entre as duas classes for linear. O problema é quando enfrentamos limites não-lineares.
O support vector machine, nesse contexto, será uma extensão do support vector classifier no sentido de ampliar o espaço utilizando para isso kernels.
Para explicar como os SVMs funcionam, vamos voltar ao problema de otimização que dá origem ao support vector classifier. A solução para aquele problema envolve apenas o produto interno das observações. De modo a relembrar, o produto interno entre dois vetores e
é definido como
. Assim, o produto interno de duas observações
será dado por
De modo que o support vector classifier pode ser representado por
onde há parâmetros
, um por observação de treino. De modo a estimar os parâmetros
e
, tudo o que precisamos será do
produtos internos
entre todos os pares de observações de treino.
Isso dito, suponha que sempre o produto interno aparecer na representação do nosso support vector classifier ou no cálculo da solução para o classificador, nós o substituímos com uma generalização do produto interno na forma
onde é uma função referida como kernel.4
Feito isso, nós podemos pegar
O que nos dá de volta o nosso classificador. A equação Equação 3 é denominada linear porque o classificador será linear nas variáveis.5
Podemos, contudo, substituir a forma de Equação 2 por
conhecido como kernel polinomial de grau . Com
, temos fronteiras de decisão mais flexíveis do que aquelas impostas pelo nosso classificador anterior. Quando nosso support vector classifier é combinado com Equação 4, nós temos como resultado o support vector machine.
Conclusão
Neste artigo mostramos como funciona o algoritmo SVM para problemas de classificação. Desenvolvemos a intuição com exemplos gráficos e mostramos aplicações para dados econômicos usando R e Python.
Quer aprender mais?
- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;
- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;
- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.
Referências
B. E. Boser, I. M. Guyon, and V. N. Vapnik. A Training Algorithm for Optimal Margin Classifiers. Annual Workshop on computacional learning, 5:144–152, July 1992.
Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
G. James, D. Witten, T. Hastie, and R. Tibshirani. An Introduction to Statistical Learning with applications in R. Springer, 2017.



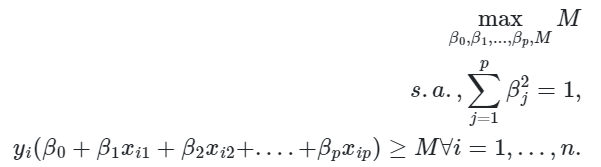
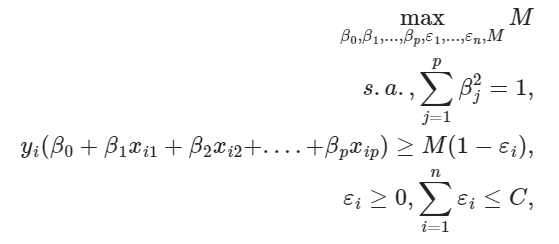
![Rendered by QuickLaTeX.com \[\left \langle x_i, x_i^{´} \right \rangle = \sum_{j=1}^{p} x_{ij} x_{ij}^{´} \label{inner}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-5306268ea6161a315e4a61353f450f54_l3.png)
![Rendered by QuickLaTeX.com \[K(x_i, x_i^{´}) = \sum_{j=1}^{p} x_{ij} x_{ij}^{´} \label{svc}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-b04928f31691e9a53811c6885cf41570_l3.png)
![Rendered by QuickLaTeX.com \[K(x_i, x_i^{´}) = (1 + \sum_{j=1}^{p} x_i, x_i^{´})^{d}, \label{kernel2}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-f681b100a10d87b73e05872c4e162d1d_l3.png)
