O Modelo de Precificação de Ativos, conhecido como CAPM (do inglês, Capital Asset Pricing Model), é uma das teorias mais fundamentais no campo da finança, essencial para a avaliação e precificação de ativos financeiros. Neste artigo, iremos mostrar como é possível analisar o CAPM para o Mercado Brasileiro usando o Python.
Desenvolvido por William Sharpe em 1964 e aprimorado por John Lintner e Jan Mossin, o CAPM desempenha um papel crucial na tomada de decisões de investimento, fornecendo uma estrutura para estimar o retorno exigido de um ativo com base em seu risco sistêmico.
Pressupostos
Para aplicar o CAPM de forma eficaz, é essencial entender seus pressupostos fundamentais:
1. Mercados Eficientes
O CAPM parte do pressuposto de que os mercados financeiros são eficientes, o que significa que todas as informações relevantes estão prontamente disponíveis e refletidas nos preços dos ativos. Portanto, os investidores não podem obter lucros anormais explorando informações privilegiadas.
2. Investidores Racionais
O modelo presume que todos os investidores são racionais e tomam decisões de investimento com base na maximização de seus retornos esperados e minimização de seus riscos.
3. Ativos Negociáveis
O CAPM se aplica apenas a ativos financeiros negociáveis, como ações e títulos, em vez de ativos reais, como imóveis ou arte.
4. Impostos e Taxas
Não há impostos, taxas ou quaisquer outras restrições para os investimentos no mercado;
Linha de Mercado de Capital e a Escolha da Carteira Eficiente
O CAPM define a relação entre o risco e o retorno esperado de um ativo em um contexto de mercado diversificado. A "Linha de Mercado de Capital" (LMC) desempenha um papel crucial no modelo. A LMC representa todas as combinações possíveis de ativos de risco (ações) e ativos sem risco (geralmente títulos do governo). Essa linha é uma representação gráfica das oportunidades de investimento disponíveis para os investidores.
A LMC define a carteira de ativos que oferece o maior retorno esperado para um nível de risco dado, ou o menor risco para um retorno esperado específico. Essa carteira é conhecida como a "Carteira Eficiente" e é o ponto de tangência entre a LMC e a curva de preferência do investidor, considerando seu nível de aversão ao risco.
CAPM
O Modelo de Precificação de Ativos (CAPM) estabelece a relação entre o retorno esperado de um ativo financeiro e seu risco sistêmico, medido pelo famoso coeficiente beta (β). O CAPM é formulado pela seguinte equação:
- : Retorno esperado do ativo.
- : Taxa livre de risco (geralmente baseada em títulos do governo).
- : Coeficiente beta do ativo, que mede seu risco sistemático em relação ao mercado.
- : Retorno esperado do mercado.
- : Prêmio de risco de mercado.
O CAPM é uma ferramenta valiosa para avaliar o desempenho de ativos, determinar seu custo de capital e tomar decisões de alocação de ativos. Ele também é usado para avaliar a eficácia de um ativo na criação de valor para os investidores, uma vez que o retorno esperado deve superar o CAPM para justificar o risco assumido.
Construindo o CAPM
Para construir o CAPM estabelecemos os seguintes dados:
- CDI mensal acumulado para a taxa livre de risco
- Retorno mensal do Ibovespa para o Retorno de Mercado
- O Retorno do ativo será de um portfólio igualmente ponderado entre as ações BBDC4, ITSA4, GGDR4 e WEGE3.
- Criamos o prêmio pelo risco, definido como excesso de retorno.
Alunos inscritos no curso de Mercado Financeiro e Gestão de Portfólio com o Python têm a oportunidade de adquirir conhecimento em todas as etapas a seguir, além de obter uma compreensão teórica abrangente das principais ferramentas utilizadas no Mercado Financeiro.
Abaixo, os retornos dos ativos utilizado.
Código
| BBDC4.SA | ITSA4.SA | VALE3.SA | WEGE3.SA | |
|---|---|---|---|---|
| Date | ||||
| 2014-02-01 | 0.043960 | 0.009941 | -0.001513 | 0.116424 |
| 2014-03-01 | 0.152414 | 0.092090 | -0.047879 | 0.045728 |
| 2014-04-01 | 0.065902 | 0.059173 | -0.059516 | 0.106488 |
| 2014-05-01 | -0.059887 | -0.038344 | -0.009714 | -0.033445 |
| 2014-06-01 | 0.027544 | 0.016374 | 0.027407 | 0.087659 |
Na tabela abaixo, os retornos construídos para os demais dados.
Código
| portfolio_ewp | retornos_ibov | cdi | excesso_retorno | excesso_ibovespa | |
|---|---|---|---|---|---|
| Date | |||||
| 2014-02-01 | 0.042203 | -0.011440 | 0.0078 | 0.034403 | -0.019240 |
| 2014-03-01 | 0.060588 | 0.070519 | 0.0076 | 0.052988 | 0.062919 |
| 2014-04-01 | 0.043012 | 0.024021 | 0.0082 | 0.034812 | 0.015821 |
| 2014-05-01 | -0.035348 | -0.007496 | 0.0086 | -0.043948 | -0.016096 |
| 2014-06-01 | 0.039746 | 0.037647 | 0.0082 | 0.031546 | 0.029447 |
Beta
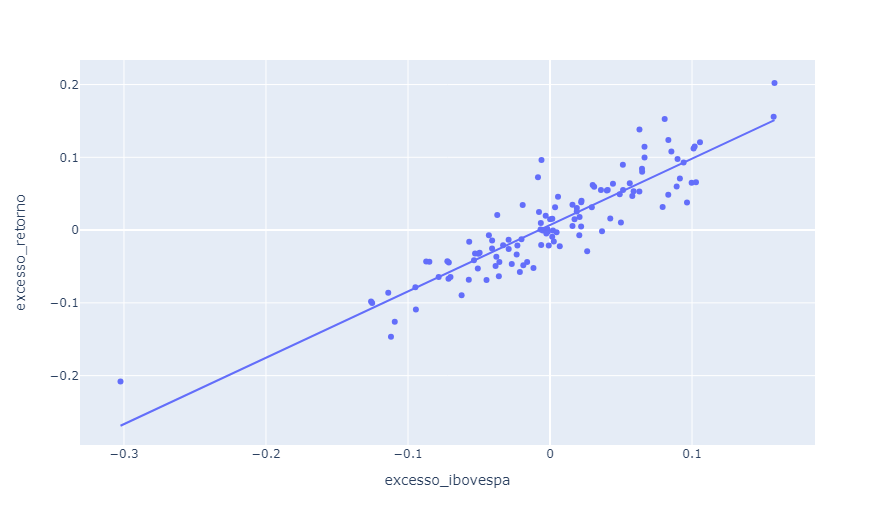
Por meio de uma regressão linear simples podemos obter o Beta de Mercado:
Código
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
Intercept 0.0070 0.003 2.573 0.011 0.002 0.012
excesso_ibovespa 0.9120 0.041 22.253 0.000 0.831 0.993
====================================================================================Gráfico de Dispersão
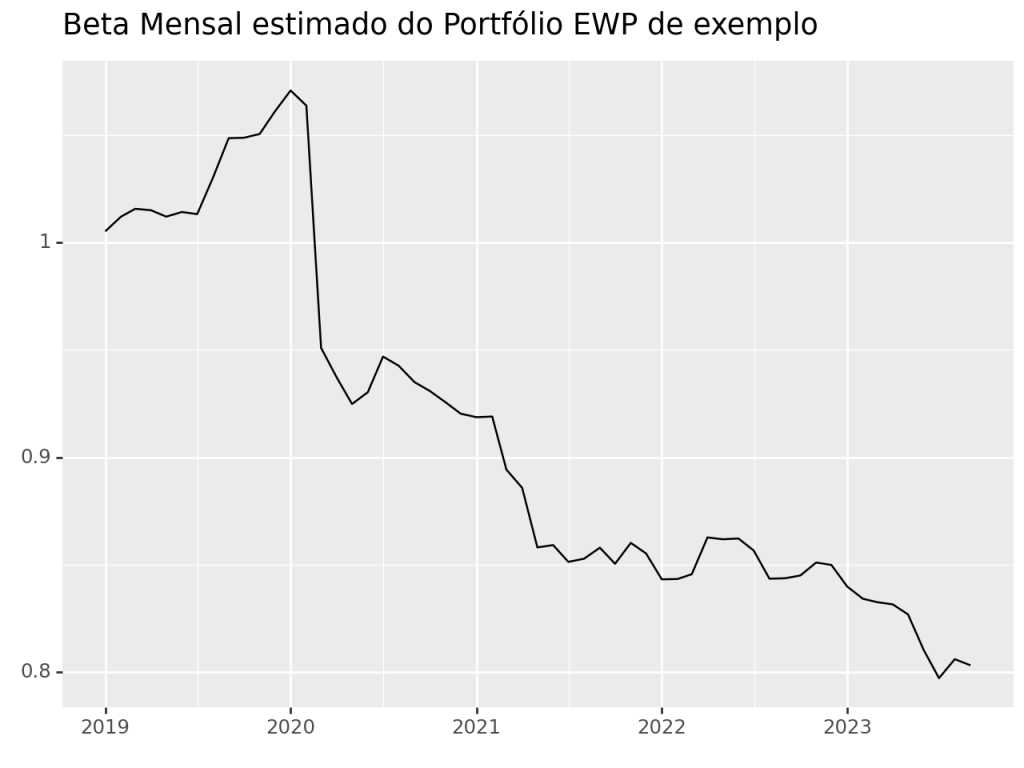
 Beta Móvel
Beta Móvel
Por fim, podemos construindo o coeficiente Beta em janelas deslizantes, isto é, construir um regressão linear para cada ponto no tempo e obter diferentes valores do Beta conforme a amostra "desliza".
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.