A maioria das pesquisas em finanças está dedicada a investigar o efeito de um anúncio da companhia ou de um evento, sistêmico ou não, sobre o preço de uma ação. Esses estudos são conhecidos como “estudos de eventos”. Neste contexto, apresentaremos uma breve introdução à metodologia e demonstraremos como aplicá-la por meio de exemplos reais utilizando a linguagem de programação Python.
A ideia inicial desses tipos de estudos tinham o intuito de verificar se os mercados eram eficientes, especificadamente a forma semiforte. A hipótese do mercado eficiente refere-se a hipotese de que os preços das ações refletem plenamente toda a informação disponível.
Como a hipótese é bem forte, foi subdividida em três categorias:
- Forma fraca: toda a informação contida nos preços históricos se reflete plenamente nos preços correntes;
- Forma semiforte: a informação disponível ao público está plenamente refletida nos preços correntes das ações;
- Forma forte: toda a informação, pública e privada, se reflete plenamente nos preços dos ativos.
Portanto, com intuito de testa a forma semiforte, o estudo de eventos busca verificar o quão rapidamente a informação divulgada é incorporada ao preço da ação.
Por exemplo, quando uma emrpesa anuncia que os dividendos serão muito maiores que o esperado, essa novidade refletirá no preço da ação no mesmo dia ou durante a próxima semana? Muitos autores utilizam o Estudo de Eventos para determinar o quão rápido a ação reage, a direção de mudança de preço e o impacto provável ocorrido.
Causalidade de um Evento
Determinar o efeito de um evento sobre uma variável pode ser algo díficil, afinal, não sabemos se de fato foi o evento que provocou a mudança. Imagine, o galo canta de manhã, e logo o sol nasce. Seria o efeito do canto que provocou o nascer do sol? Esse caso parece ser óbvio, mas muito vezes a dificuldade está nessa questão. Pense bem no caso de anúncio de dividendos, e se em um momento próximo a esse evento ter ocorrido outro evento significativo? Como podemos lidar com essa situação?
Estudos que envolvem verificar a causalidade são rigorosos, e usualmente fazem a separação de dois grupos: controle e tratamento, com o intuito de comparar os efeitos. O grupo de controle refere-se aquele conjunto que não é submetido a um experimento, enquanto o de tratamento recebe a intervenção.
Mas vejam bem, como podemos fazer o controle de uma variável que é difícil de se realizar em um experimento controlado? (afinal, não é possível provocar um evento de propósito no mercado financeiro para fins de pesquisa), e principalmente, uma variável que se move ao longo do tempo, e está sujeita a n diferentes eventos.
Todo o design de um estudo de eventos é baseado na ideia de que algo muda ao longo do tempo - o evento ocorre, o tratamento entra em vigor. Então, podemos comparar o antes do evento com o depois do evento e obter o efeito do tratamento. No entanto, precisamos que o tratamento seja a única coisa que está mudando. Se o resultado fosse mudar de qualquer maneira por algum outro motivo e não o considerarmos, o estudo de eventos não será bem-sucedido.
Aqui está a parte complicada. Afinal, as coisas estão sempre mudando ao longo do tempo. Então, como podemos ter certeza de que removemos todas as maneiras pelas quais o tempo afeta o resultado, exceto por aquela parte extremamente importante que queremos manter, o momento em que passamos do antes do evento para o depois do evento?
Em resumo, temos que ter alguma maneira de prever o contrafactual. Temos muitas informações sobre a variável e seus dados antes do evento. Se pudermos fazer uma suposição de que o que estava acontecendo antes teria continuado se não fosse pelo tratamento, então podemos usar esses dados do antes do evento para prever o que esperaríamos ver sem o tratamento e, em seguida, ver como o resultado real se desvia dessa previsão. A extensão da discrepância é o efeito do tratamento.
Temos 3 formas de realizar esse procedimento:
- Comparar os antes e depois do evento, sem qualquer controle;
- Prever os valores de depois do evento usando dados antes do evento;
- Comparar os depois do evento com algum “benchmark”.
Veremos como construir o Estudo de Eventos.
Metodologia dos Estudos de Eventos
Como criar o contrafactual?
Podemos estimar através de alguns procedimentos:
- Retorno esperado pela média amostral
- Retorno esperado igual ao retorno de mercado
- Retorno esperado por meio de um modelo: Modelo de Mercado, CAPM, 3 e 5 fatores de fama-french.
Exemplo: Ações do Google
Em 10 de agosto de 2015, o Google anunciou que estaria reorganizando sua estrutura corporativa. Não mais seria “Google” proprietário de várias outras empresas, como FitBit e Nest, mas em vez disso haveria uma nova empresa-mãe chamada “Alphabet” que seria a proprietária do Google, juntamente com todas as outras subsidiárias.
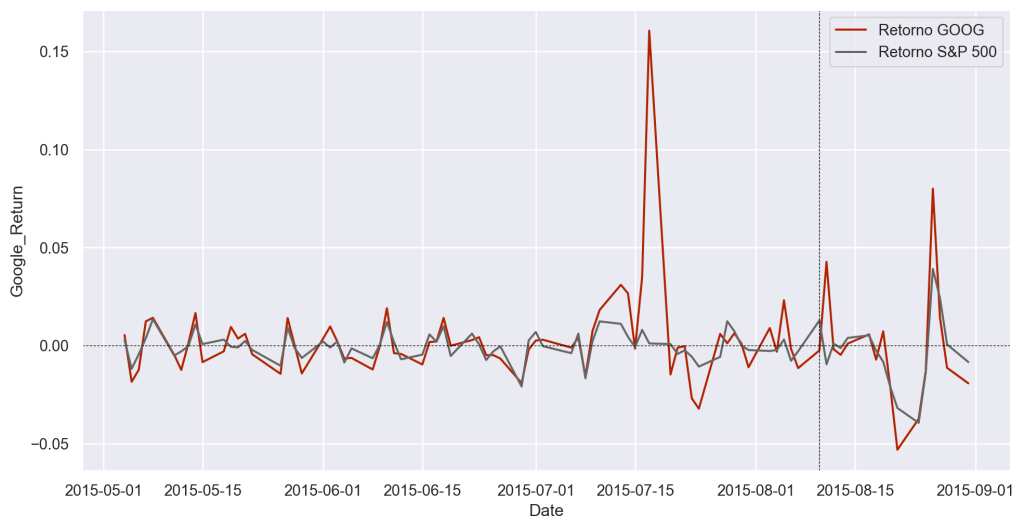
Como o mercado de ações reagiu a isso? Para descobrir, usamos dados sobre o preço das ações da GOOG de maio de 2015 até o final de agosto de 2015. Também pegamos os dados do preço do índice S&P 500 para usá-lo como medida de índice de mercado.
Em seguida, calculamos o retorno diário para a GOOG e para o S&P 500. Por que usar retornos em vez do preço? Porque estamos interessados em ver como a nova informação afeta o preço, então é melhor isolar essas mudanças para que possamos examiná-las. Olhar para os retornos também facilita a comparação de ações com preços muito diferentes.
Vamos pegar os dados e verificar visualmente o gráfico de ambos os retornos no período.
Vamos agora criar o Estudo de Eventos. Tomando como base 3 formas de ajustar os retornos anormais, verificamos os resultados no gráfico abaixo:
Conforme a metodologia, podemos considerar que houve uma mudança positiva no preço da ação da GOOG devido o evento.
Exemplo: Event Study
A biblioteca EventStudy do Python oferece suporte essencial no desenvolvimento de Estudos de Eventos, disponibilizando funções que facilitam a previsão de retornos e retornos anormais.
A título de exemplo, analisaremos o impacto do anúncio do primeiro iPhone, realizado por Steve Jobs em 7 de janeiro de 2007. Para calcular os retornos anormais, compararemos os retornos efetivos da Apple com os retornos estimados através do modelo de três fatores de Fama-French.
Abaixo os dados de retornos de empresas de tecnologia, e o um benchmark apropriado para o set (SPY).
Código
| date | AAPL | AMZN | FB | GOOG | MSFT | SPY | |
|---|---|---|---|---|---|---|---|
| 0 | 2000-01-03 | 0.088754 | 0.174056 | NaN | NaN | -0.001606 | -0.009787 |
| 1 | 2000-01-04 | -0.084310 | -0.083217 | NaN | NaN | -0.033780 | -0.039106 |
| 2 | 2000-01-05 | 0.014634 | -0.148741 | NaN | NaN | 0.010544 | 0.001789 |
| 3 | 2000-01-06 | -0.086538 | -0.060036 | NaN | NaN | -0.033498 | -0.016071 |
| 4 | 2000-01-07 | 0.047368 | 0.061010 | NaN | NaN | 0.013068 | 0.058076 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 5025 | 2019-12-23 | 0.016318 | 0.003638 | -0.000582 | -0.000556 | 0.000000 | 0.001528 |
| 5026 | 2019-12-24 | 0.000951 | -0.002114 | -0.005141 | -0.003914 | -0.000191 | 0.000031 |
| 5027 | 2019-12-26 | 0.019840 | 0.044467 | 0.013017 | 0.012534 | 0.008197 | 0.005323 |
| 5028 | 2019-12-27 | -0.000379 | 0.000551 | 0.001492 | -0.006256 | 0.001828 | -0.000248 |
| 5029 | 2019-12-30 | 0.005935 | -0.012253 | -0.017732 | -0.011650 | -0.008619 | -0.005513 |
5030 rows × 7 columns
Para computar o Retorno Anormal, estimaremos a previsão dos retornos conforme o Modelo de 3 fatores de fama-french, conforme os dados abaixo.
Código
| date | Mkt-RF | SMB | HML | RF | |
|---|---|---|---|---|---|
| 0 | 1926-07-01 | 0.10 | -0.24 | -0.28 | 0.009 |
| 1 | 1926-07-02 | 0.45 | -0.32 | -0.08 | 0.009 |
| 2 | 1926-07-06 | 0.17 | 0.27 | -0.35 | 0.009 |
| 3 | 1926-07-07 | 0.09 | -0.59 | 0.03 | 0.009 |
| 4 | 1926-07-08 | 0.21 | -0.36 | 0.15 | 0.009 |
| ... | ... | ... | ... | ... | ... |
| 24574 | 2019-09-24 | -1.01 | -0.73 | -0.02 | 0.009 |
| 24575 | 2019-09-25 | 0.69 | 0.36 | 0.56 | 0.009 |
| 24576 | 2019-09-26 | -0.41 | -0.96 | 0.11 | 0.009 |
| 24577 | 2019-09-27 | -0.62 | -0.35 | 0.88 | 0.009 |
| 24578 | 2019-09-30 | 0.50 | -0.14 | -0.49 | 0.009 |
24579 rows × 5 columns
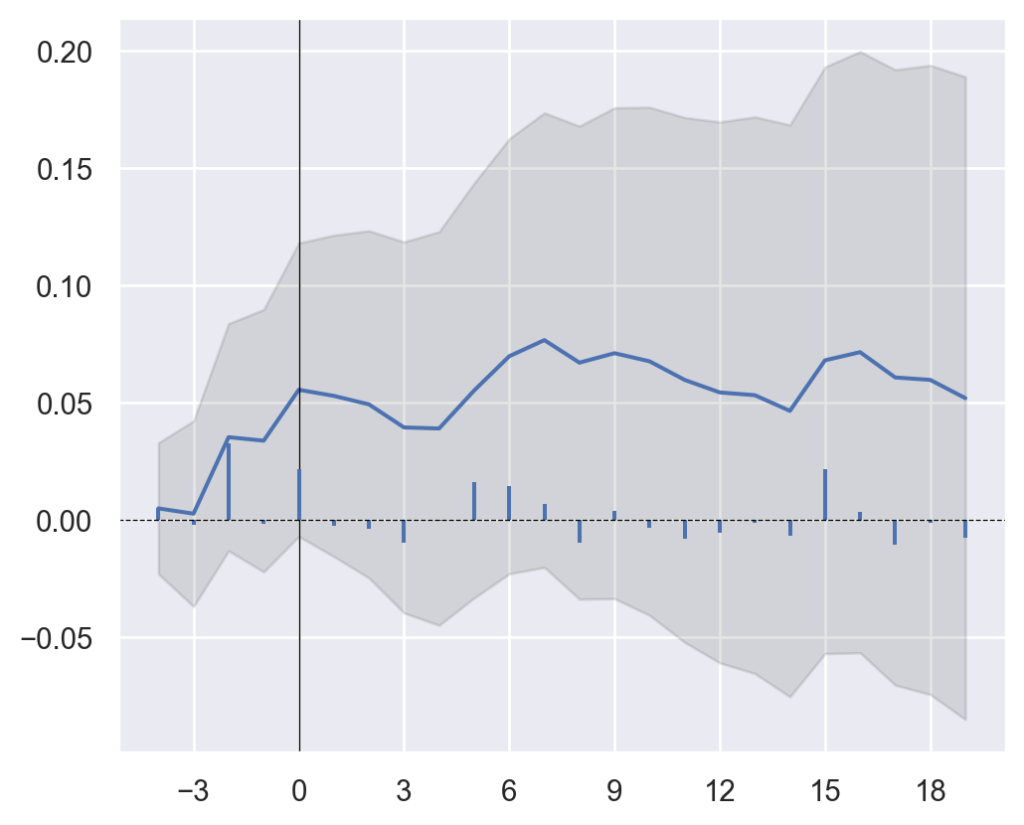
Abaixo temos o resultado do Retorno Anormal Acumulado (linha azul) e o Retorno Anormal (barras azuis). A parte cinza refere-se ao intervalo de confiança do Retorno Anormal Acumulado.
Código
| AR | Std. E. AR | CAR | Std. E. CAR | T-stat | P-value | |
|---|---|---|---|---|---|---|
| -4 | 0.005 | 0.02179 | 0.005 | 0.02179 | 0.23 | 0.82 |
| -3 | -0.002 | 0.02179 | 0.003 | 0.03081 | 0.09 | 0.93 |
| -2 | 0.033 | 0.02179 | 0.035 | 0.03774 | 0.94 | 0.35 |
| -1 | -0.001 | 0.02179 | 0.034 | 0.04357 | 0.78 | 0.44 |
| 0 | 0.022 | 0.02179 | 0.056 | 0.04872 | 1.14 | 0.26 |
| 1 | -0.003 | 0.02179 | 0.053 | 0.05337 | 0.99 | 0.32 |
| 2 | -0.004 | 0.02179 | 0.049 | 0.05764 | 0.86 | 0.39 |
| 3 | -0.010 | 0.02179 | 0.039 | 0.06162 | 0.64 | 0.52 |
| 4 | -0.000 | 0.02179 | 0.039 | 0.06536 | 0.60 | 0.55 |
| 5 | 0.016 | 0.02179 | 0.055 | 0.06890 | 0.80 | 0.42 |
| 6 | 0.015 | 0.02179 | 0.07 | 0.07226 | 0.97 | 0.33 |
| 7 | 0.007 | 0.02179 | 0.077 | 0.07547 | 1.02 | 0.31 |
| 8 | -0.010 | 0.02179 | 0.067 | 0.07855 | 0.85 | 0.39 |
| 9 | 0.004 | 0.02179 | 0.071 | 0.08152 | 0.87 | 0.38 |
| 10 | -0.003 | 0.02179 | 0.068 | 0.08438 | 0.80 | 0.42 |
| 11 | -0.008 | 0.02179 | 0.06 | 0.08715 | 0.69 | 0.49 |
| 12 | -0.005 | 0.02179 | 0.054 | 0.08983 | 0.61 | 0.55 |
| 13 | -0.001 | 0.02179 | 0.053 | 0.09244 | 0.58 | 0.57 |
| 14 | -0.007 | 0.02179 | 0.047 | 0.09497 | 0.49 | 0.62 |
| 15 | 0.022 | 0.02179 | 0.068 | 0.09744 | 0.70 | 0.49 |
| 16 | 0.003 | 0.02179 | 0.072 | 0.09984 | 0.72 | 0.47 |
| 17 | -0.011 | 0.02179 | 0.061 | 0.10219 | 0.59 | 0.55 |
| 18 | -0.001 | 0.02179 | 0.06 | 0.10449 | 0.57 | 0.57 |
| 19 | -0.008 | 0.02179 | 0.052 | 0.10673 | 0.49 | 0.63 |
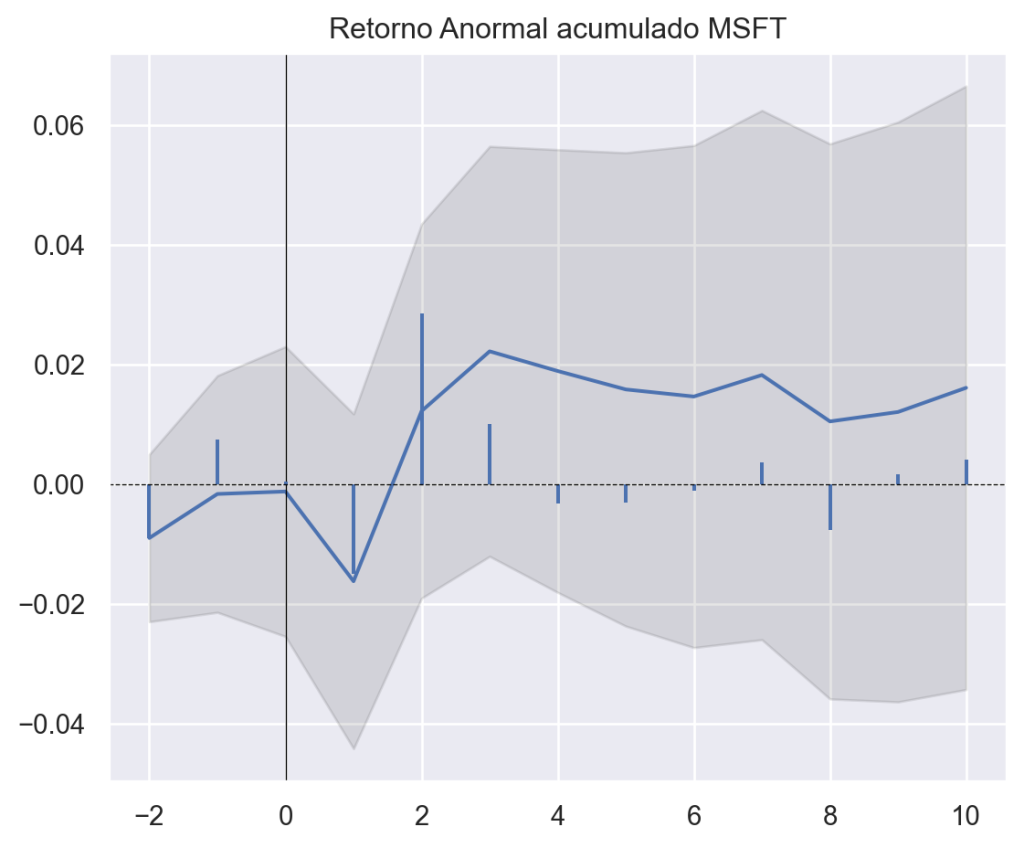
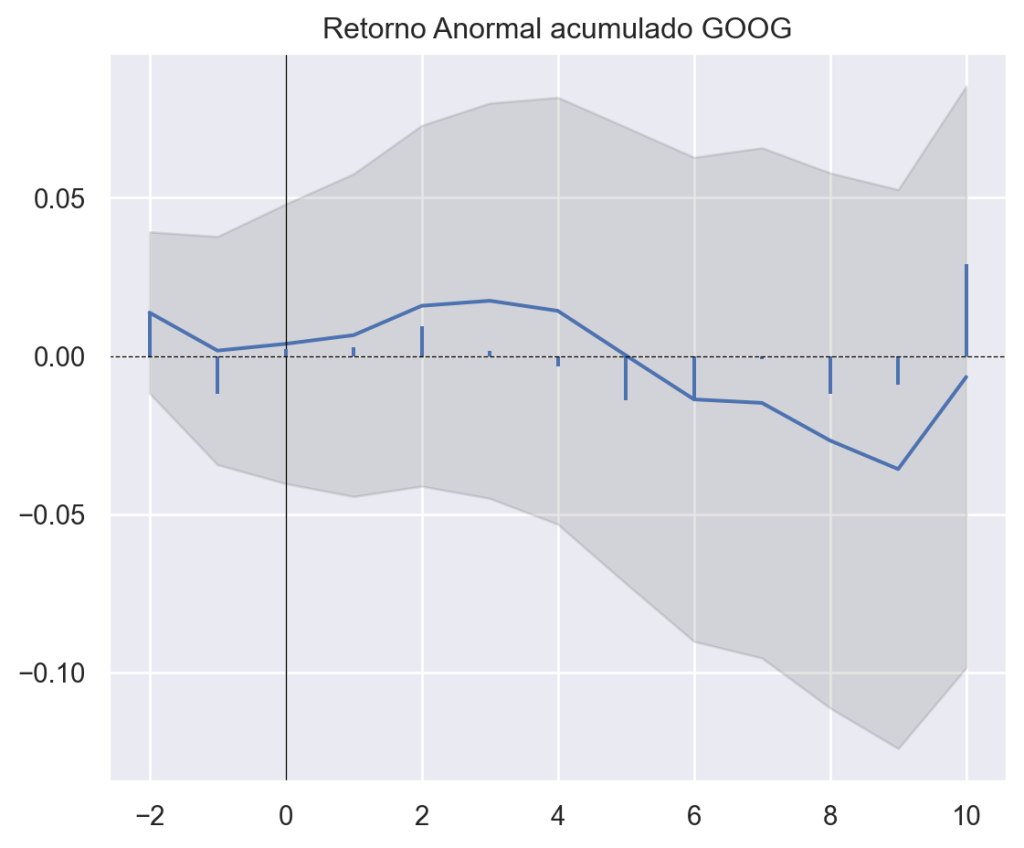
Por fim, podemos criar diversos diversos Eventos, seja para diferentes empresas, seja para diferentes datas de evento. Abaixo, comparamos os efeito do evento sobre o Retornos da AAPL, MSFT e GOOG.
Referências
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.