Qual é a importância de choques na inflação na origem dos erros de previsão da Selic? Analisando a decomposição da variância no VAR

Uma nova guerra estoura no outro lado do Atlântico em uma área produtora global de energia, o preço do barril de petróleo dispara e, eventualmente, o preço da gasolina, do arroz, do feijão e de outros produtos e serviços na cesta de inflação brasileira também sobem. Com surpresas inflacionárias e um cenário de riscos maior, o Banco Central tem mais trabalho na condução da política monetária e na decisão sobre a taxa básica de juros da economia. Consequentemente, os economistas podem errar mais sobre a trajetória futura da taxa de juros.

Se essa linha de raciocínio é válida, como mensurar a importância de choques na inflação — como o descrito acima — sobre o erro de previsão da taxa de juros? Para responder esta questão, neste exercício quantificamos esta relação sob a ótica de um modelo VAR, usando dados recentes da macroeconomia brasileira. Especificamente, estimamos a decomposição da variância dos erros de previsão do modelo, analisando choques na inflação da gasolina e sua importância sobre a variância dos erros de previsão da taxa Selic.

Modelo

Com o propósito de quantificar a decomposição da variância dos erros de previsão entre choques no preço da gasolina e a relação na taxa Selic, estimamos um modelo VAR, como abaixo:

$y_t = \sum_{i\ge0}^p A_p y_{t-p} + z_t + \varepsilon_t$

onde:

$y_t = (\pi_t^G, \Delta P_t, \Delta e_t, \Delta \gamma_t, \Delta i_t)$
$\pi_t^G$ é a inflação do preço da gasolina do IPCA
$\Delta P_t$ é a variação do preço internacional do barril de petróleo em dólares¹
$\Delta e_t$ é a variação da taxa de câmbio nominal (R$/US$)¹
$\Delta\gamma_t$ é a variação do indicador de incerteza da economia brasileira¹
$\Delta i_t$ é a variação da taxa de juros Selic¹
$z_t$ é uma variável de controle que pode incluir constante, tendência e/ou dummies sazonais

¹Sobre estas variáveis foram aplicadas primeiro esta transformação: $f(x)=\frac{x^{0.2}-1}{0.2}$ .

Decomposição da variância dos erros de previsão

A decomposição da variância dos erros de previsão (DV) responde a seguinte pergunta:

Quais parcelas da variância do erro de previsão de um modelo VAR, em um dado horizonte de tempo $h$ , são decorrentes de quais choques estruturais (erros)?

Dessa forma, a DV permite analisar a importância relativa de cada choque individual sobre variância do erro de previsão de uma variável endógena em um modelo VAR. Para uma formalização sobre como calcular a DV veja, por exemplo, Wikipedia (2022).

Dados

Para obter o código deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

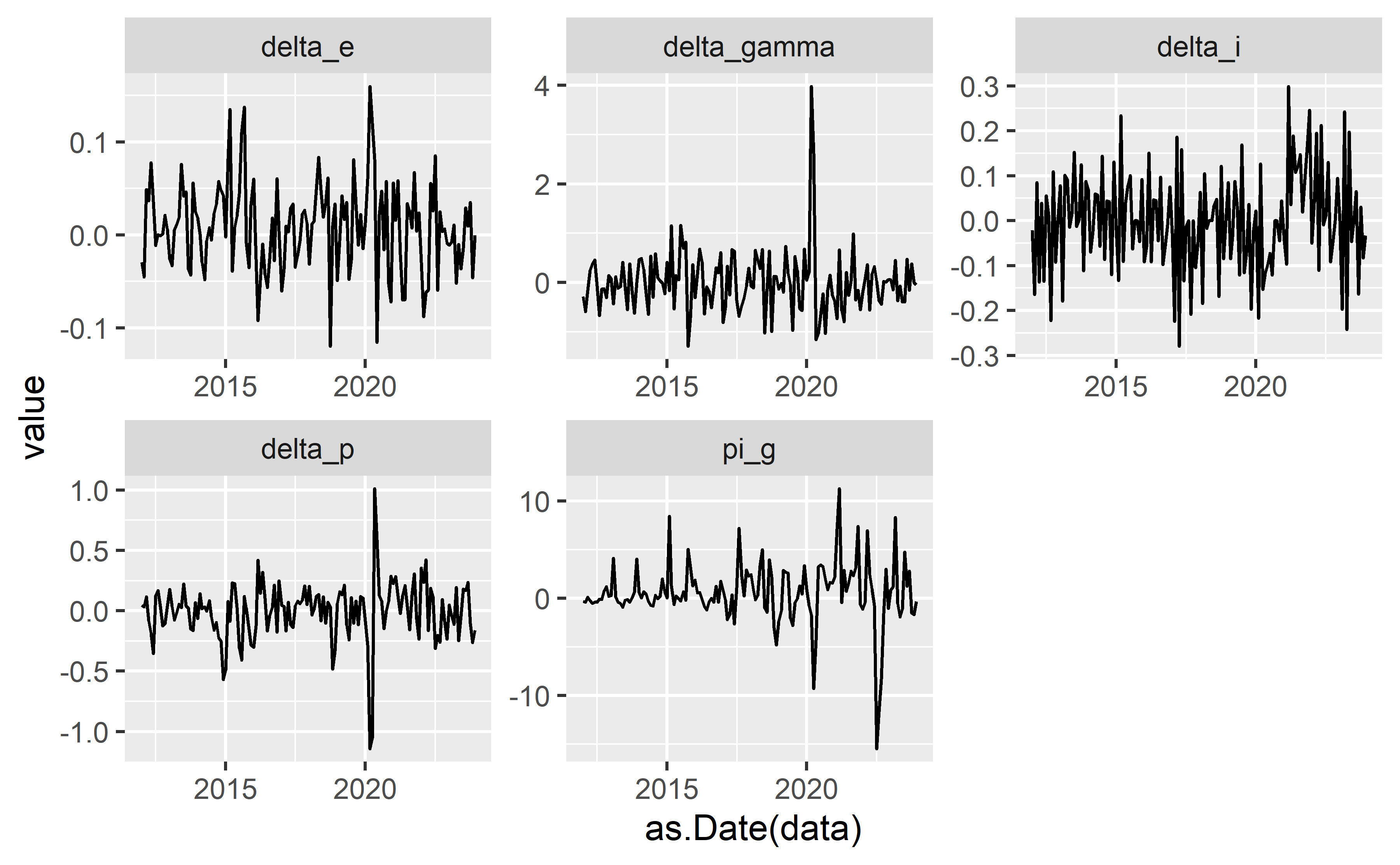
Utilizamos uma amostra de dados de janeiro de de 2012 até dezembro de 2023. Os dados em frequência mensal são expostos no gráfico abaixo:

Exploração

Confirmamos a ordem de integração das séries através de testes de estacionariedade ADF, PP e KPSS com constante e com tendência. Como são 3 testes e 2 especificações possíveis, foram aplicados 6 testes individualmente para cada variável. Abaixo reportamos a ordem de integração mais frequentemente reportada entre os testes para cada variável:

# A tibble: 5 × 3
  variavel    ordem_integracao     n
  <chr>                  <dbl> <int>
1 delta_e                    0     6
2 delta_gamma                0     6
3 delta_i                    0     5
4 delta_p                    0     6
5 pi_g                       0     6

Encontramos que todas as variáveis são integradas de ordem 0.

Modelagem

Neste cenário, prosseguimos com a estimação de um modelo VAR(p), sendo a ordem de defasagens p definida por critérios de informação, com um mínimo de 3 defasagens para eliminar autocorrelações seriais. Abaixo exibimos os resultados da equação da taxa de juros Selic no sistema VAR:

Call:
lm(formula = y ~ -1 + ., data = datamat)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.171541 -0.039560  0.001745  0.033824  0.131572 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
pi_g.l1         0.002458   0.002275   1.080 0.282268    
delta_p.l1      0.015881   0.029873   0.532 0.596033    
delta_e.l1      0.091710   0.147950   0.620 0.536582    
delta_gamma.l1 -0.018294   0.012388  -1.477 0.142493    
delta_i.l1     -0.245969   0.068141  -3.610 0.000457 ***
pi_g.l2         0.003403   0.002542   1.339 0.183363    
delta_p.l2     -0.004561   0.031359  -0.145 0.884627    
delta_e.l2      0.413867   0.152255   2.718 0.007588 ** 
delta_gamma.l2 -0.017728   0.012255  -1.447 0.150734    
delta_i.l2      0.264962   0.066613   3.978 0.000123 ***
pi_g.l3        -0.002008   0.002243  -0.895 0.372550    
delta_p.l3      0.052523   0.030622   1.715 0.089022 .  
delta_e.l3     -0.175910   0.147230  -1.195 0.234648    
delta_gamma.l3 -0.003035   0.012643  -0.240 0.810705    
delta_i.l3      0.650159   0.067296   9.661  < 2e-16 ***
const          -0.004584   0.005888  -0.778 0.437920    
sd1            -0.071706   0.029750  -2.410 0.017539 *  
sd2            -0.172088   0.028483  -6.042 1.96e-08 ***
sd3            -0.003205   0.029538  -0.109 0.913787    
sd4            -0.078236   0.032491  -2.408 0.017646 *  
sd5             0.028086   0.030778   0.913 0.363423    
sd6            -0.143580   0.033094  -4.339 3.12e-05 ***
sd7            -0.006158   0.028559  -0.216 0.829671    
sd8            -0.087352   0.030684  -2.847 0.005239 ** 
sd9            -0.154329   0.027615  -5.589 1.58e-07 ***
sd10           -0.106734   0.029068  -3.672 0.000368 ***
sd11           -0.116732   0.028842  -4.047 9.47e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.06387 on 114 degrees of freedom
Multiple R-squared:  0.7397,    Adjusted R-squared:  0.6803 
F-statistic: 12.46 on 26 and 114 DF,  p-value: < 2.2e-16

De modo a avançar, diagnosticamos a especificação do modelo VAR com os testes de autocorreção, normalidade e heterocedasticidade, conforme resultados abaixo:

# Autovalores

 [1] 0.8878060 0.8693959 0.8693959 0.6666014 0.6666014 0.5686225 0.5686225
 [8] 0.5295016 0.5295016 0.4494450 0.4149401 0.4149401 0.3072341 0.1841566
[15] 0.1841566

# Teste de autocorrelação

    Portmanteau Test (asymptotic)

data:  Residuals of VAR object modelo_var
Chi-squared = 352.88, df = 325, p-value = 0.1379

# Teste de normalidade
vars::normality.test(modelo_var)

Skewness

    Skewness only (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 15.337, df = 5, p-value = 0.009015


$Kurtosis

    Kurtosis only (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 312.49, df = 5, p-value < 2.2e-16

# Teste para heterocedasticidade

    ARCH (multivariate)

data:  Residuals of VAR object modelo_var
Chi-squared = 1198.9, df = 1125, p-value = 0.06188

Os resíduos do modelo são homocedásticos e não autocorrelacionados, porém não são normalmente distribuídos a 5% de significância. As séries temporais apresentam outliers, característico de dados econômicos. Dessa forma, mesmo com transformações e/ou dummies é um desafio atingir a normalidade destas variáveis. Ignoraremos este problema aqui, enfatizando que intervalos de confiança calculados a partir deste modelo podem ser imprecisos.

Análise de decomposição da variância

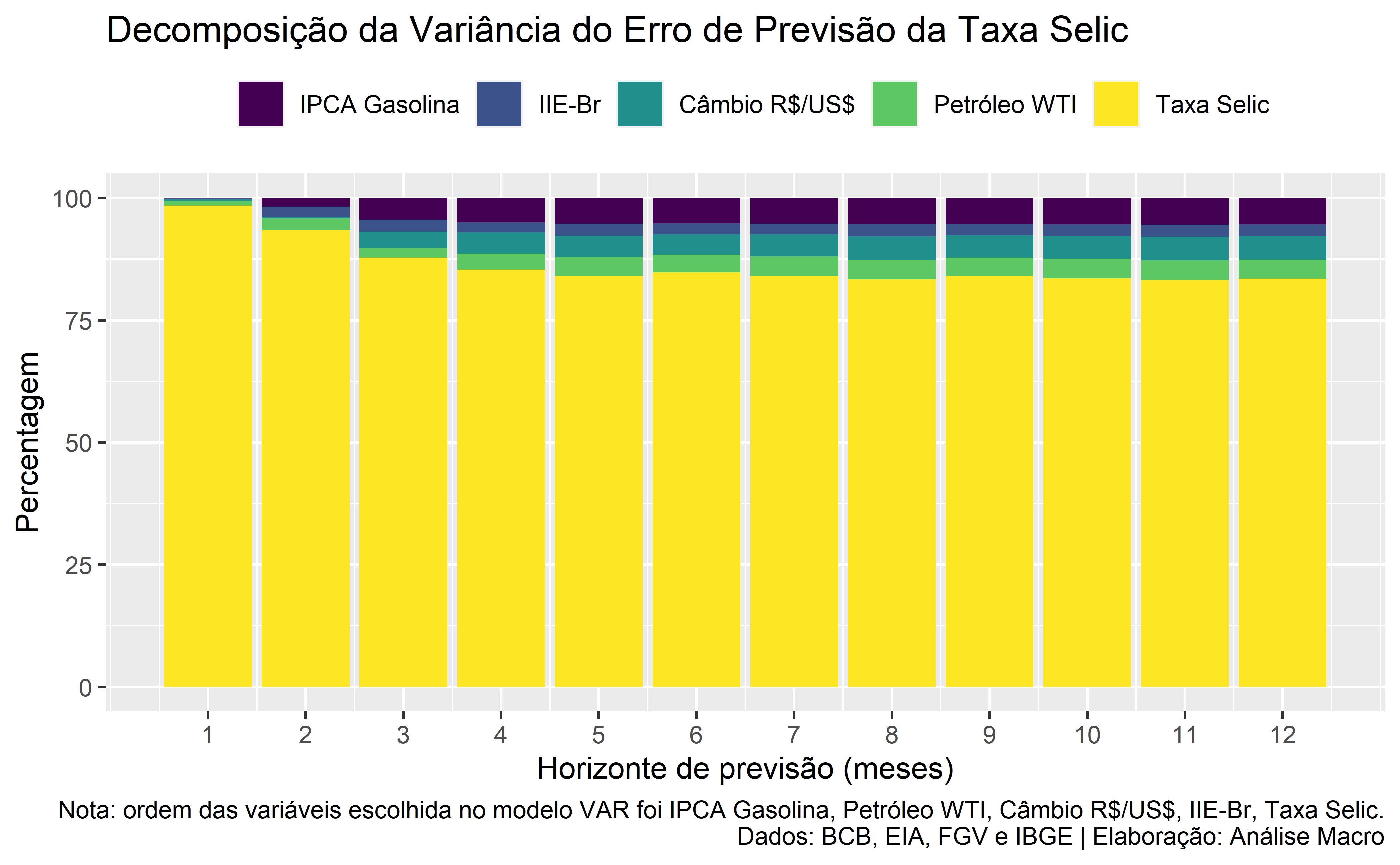
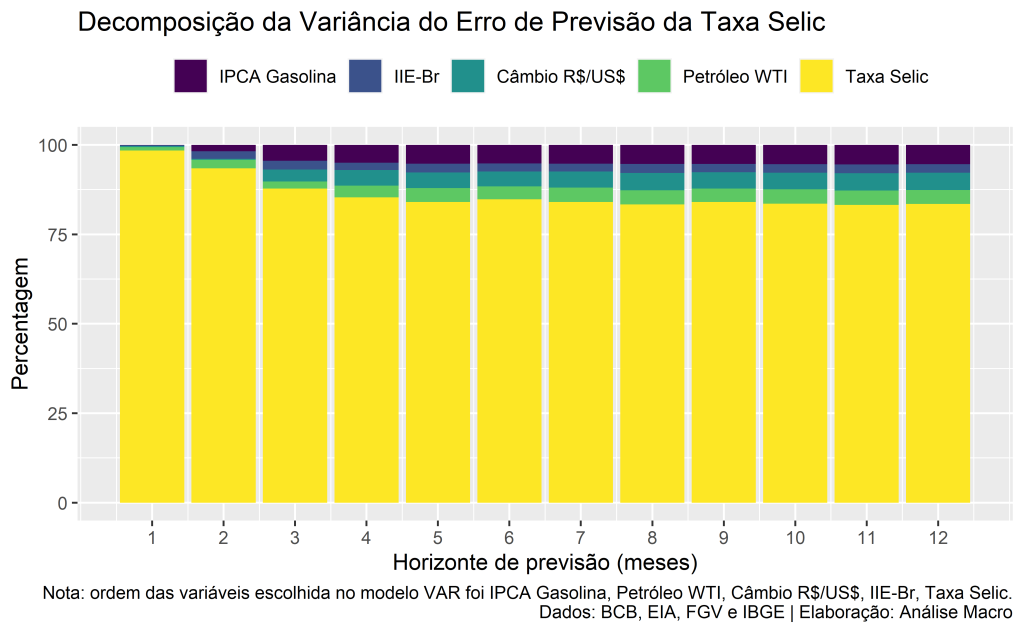
Com este modelo, estimamos a decomposição da variância, focando na análise da importância dos choques na inflação da gasolina para explicar os erros de previsão da taxa Selic . O gráfico de resultado é exposto abaixo:

Decompondo a variância do erro de previsão da taxa Selic em contribuições individuais de choques nas variáveis do sistema VAR, podemos destacar os principais resultados:

Percebe-se que a a própria Selic é a variável mais importante em explicar seus erros de previsão (suavização da política monetária?);
No primeiro período, 98% da variância do erro de previsão da Selic se deve a choques na própria Selic;
A importância da Selic na DV é persistente ao longo do tempo, seja no curto ou no longo prazo, decaindo suavemente no horizonte considerado;
A partir do segundo período, choques em outras variáveis começam a ganhar importância, com destaque para o IPCA Gasolina e Petróleo que explicam, juntos 9% da variância do erro de previsão da Selic no 12º período;
O sistema torna-se estável após o 4º ou 5º período.

Conclusão

Como mensurar a importância de choques na inflação sobre o erro de previsão da taxa de juros? Neste exercício quantificamos esta pergunta sob a ótica de um modelo VAR, usando dados recentes da macroeconomia brasileira. Especificamente, estimamos a decomposição da variância dos erros de previsão do modelo, analisando choques na inflação da gasolina e sua importância sobre a variância dos erros de previsão da taxa Selic.

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Referências

Wikipedia contributors. (2022, June 7). Variance decomposition of forecast errors. In Wikipedia, The Free Encyclopedia. Retrieved 15:54, January 11, 2024, from https://en.wikipedia.org/w/index.php?title=Variance_decomposition_of_forecast_errors&oldid=1091939135

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Propensity Score com Múltiplas Variáveis no R

Análise regional da inflação com dados do IBGE usando Python

Como coletar dados do Banco Central do Chile usando a API com o Python?

Como analisar a relação de risco-retorno de ações?

Retropolando a série do desemprego no Brasil

Variáveis Instrumentais no R: qual o impacto do gasto de segurança no crime?

Outros artigos relacionados

Propensity Score com Múltiplas Variáveis no R

O escore de propensão é provavelmente a maneira mais comum de agregar múltiplas variáveis de correspondência em um único valor que pode ser correspondido, ou seja, muito útil para a realização de pareamento.

O escore de propensão é a probabilidade estimada de que uma determinada observação teria sido tratada. A correspondência de escore de propensão muitas vezes significa selecionar um conjunto de observações de controle correspondidas com valores semelhantes do escore de propensão.

Análise regional da inflação com dados do IBGE usando Python

Os dados desagregados do IPCA fornecem informações detalhadas sobre o comportamento de preços no Brasil a nível de região metropolitana e município, possibilitando ricas análises regionais de dados. Neste artigo mostramos como acessar, processar e analisar estes dados utilizando o Python.

Como coletar dados do Banco Central do Chile usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal do Banco Central do Chile através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.