O que é e como estimar o Beta de uma ação usando o Python

O beta, também conhecido como coeficiente beta (β), é uma medida que quantifica a sensibilidade de um ativo financeiro em relação às variações do mercado como um todo. Em outras palavras, o beta indica o grau de volatilidade de um ativo em relação ao movimento de um índice de referência. Neste artigo, vamos explorar em detalhes o funcionamento do coeficiente beta e demonstrar como obtê-lo utilizando um conjunto de dados do mercado acionário brasileiro. Utilizaremos a linguagem de programação Python como ferramenta para construção e análise.

O beta, também conhecido como coeficiente beta (β), é uma medida que quantifica a sensibilidade de um ativo financeiro em relação às variações do mercado como um todo. Em outras palavras, o beta indica o grau de volatilidade de um ativo em relação ao movimento de um índice de referência.

Neste artigo, vamos explorar em detalhes o funcionamento do coeficiente beta e demonstrar como obtê-lo utilizando um conjunto de dados do mercado acionário brasileiro. Utilizaremos a linguagem de programação Python como ferramenta para construção e análise.

Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Aprenda a coletar, processar e analisar dados do mercado financeiro no curso de Mercado Financeiro e Gestão de Portfólio usando o Python.

Modelo de Índice Único

Empiricamente foi observado no mercado acionário que, quando o mercado sobe (mensurado por um índice de bolsa de valores), a maioria das ações tende a aumentar o preço e, quando o mercado cai, a maioria das ações vê seu preço diminuir. Isso sugere o motivo da correlação entre as ações, que deriva do fato que há uma resposta comum a mudanças de mercado.

O retorno de uma ação pode ser escrito como:

$R_i = \alpha_i + \beta_i R_m + e_i$

- $R_i$ : Retorno do ativo

- $\alpha_i$ : Representa o valor esperado do retorno não oriundo do mercado

- $R_m$ : Retorno do índice de mercado

- $\beta_i$ : Mede a mudança esperada em $R_i$ dada uma mudança em $R_m$

- $e_i$ : É o componente aleatório que afeta os retornos.

CAPM

O Modelo de Precificação de Ativos (CAPM) estabelece uma relação sistemática de precificação de ações, a partir da concepção da arbitragem de risco entre o retorno esperado de um ativo financeiro e seu risco sistêmico, medido pelo famoso coeficiente beta (β). A formulação do CAPM foi independente da resolução do modelo de índice única, apesar da semelhança. O CAPM é formulado pela seguinte equação:

$E(R_i) = R_f + \beta_i (E(R_m) - R_f)$

- $E(R_i)$ : Retorno esperado do ativo.
- $R_f$ : Taxa livre de risco (geralmente baseada em títulos do governo).
- $\beta_i$ : Coeficiente beta do ativo, que mede seu risco sistemático em relação ao mercado.
- $E(R_m)$ : Retorno esperado do mercado.
- $E(R_m) - R_f$ : Prêmio de risco de mercado.

Beta

- Um ativo com $\beta = 1$ é considerado tão volátil quanto o mercado. Isso significa que, em média, ele se move na mesma direção e na mesma proporção que o mercado.

- Um ativo com $\beta > 1$ é considerado mais volátil que o mercado. Isso significa que, em média, ele tende a ter movimentos maiores do que o mercado.

- Um ativo com $\beta < 1$ é considerado menos volátil que o mercado. Isso significa que, em média, ele tende a ter movimentos menores do que o mercado.

- Um ativo com $\beta = 0$ é considerado não relacionado ao mercado. Isso significa que seus retornos são independentes dos movimentos do mercado.

Podemos estimar o Beta a partir da seguinte fórmula:

$\beta = \frac{{\text{Covariância}(R_i, R_m)}}{{\text{Variância}(R_m)}}$

Assim, podemos obter a estimativa pela forma manual, calculando a covariância e a variância, ou usando funções para o cálculo do MQO.

Estimando o Beta no Python

Para obter a estimativa do Beta necessitamos de retornos dos ativos, do retorno de mercado e um taxa representa a taxa livre de risco. Aqui usaremos quatro ações para definir um portfólio teórico com pesos iguais ('BBDC4.SA', 'ITSA4.SA', 'VALE3.SA', 'WEGE3.SA'). Usaremos o retorno do Ibovespa como retorno de mercado e o CDI como taxa livre de risco. Os dados compreendem o período de jan/2014 até dez/2023 em periodicidade mensal.

Os valores iniciais do conjunto dados utilizados para o modelo estão dispostos na tabela abaixo:

Código

	portfolio_ewp	retornos_ibov	cdi	excesso_retorno	excesso_ibovespa
Date
2014-02-01	0.042203	-0.011440	0.0078	0.034403	-0.019240
2014-03-01	0.060588	0.070519	0.0076	0.052988	0.062919
2014-04-01	0.043038	0.024021	0.0082	0.034838	0.015821
2014-05-01	-0.035348	-0.007496	0.0086	-0.043948	-0.016096
2014-06-01	0.039746	0.037647	0.0082	0.031546	0.029447

Regressão Linear

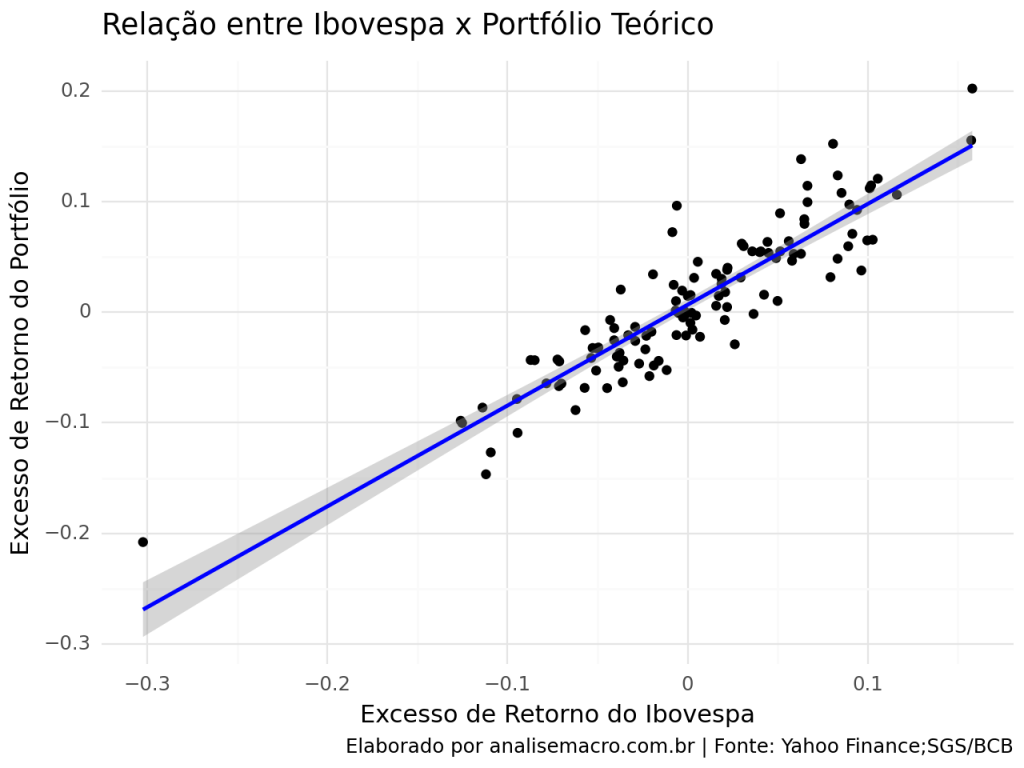
Por meio de uma regressão linear simples via MQO chegamos ao resultado de um alpha no valor de 0.0069 e um Beta de 0.9124.

Código

====================================================================================
                       coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------
Intercept            0.0069      0.003      2.596      0.011       0.002       0.012
excesso_ibovespa     0.9124      0.040     22.867      0.000       0.833       0.991
====================================================================================

Gráfico de Dispersão

O gráfico de dispersão permite estabelecer a relação entre os excessos de retornos.

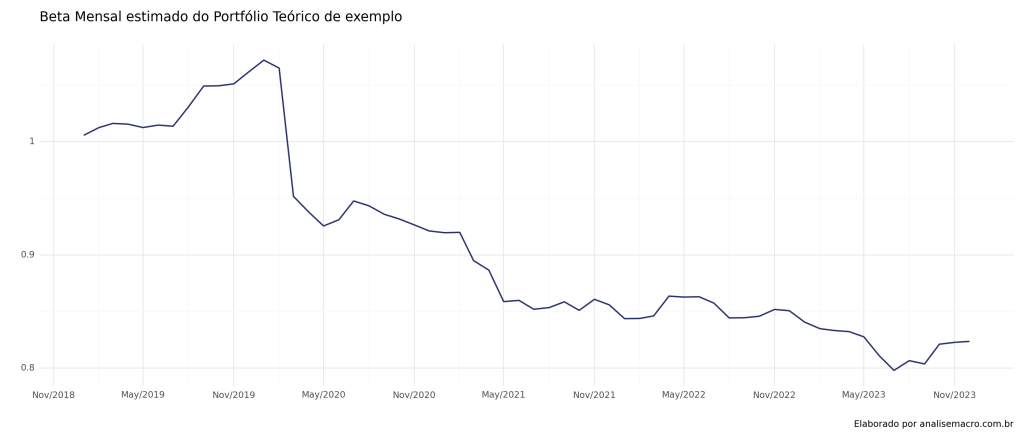
Beta Móvel

O Beta Móvel é criado a partir da estimação do MQO em janelas deslizantes em períodos de 60 meses. Isso significa que podemos construir o beta a cada periodo de tempo, buscando compreender a dinâmica da relação entre o portfólio e o risco sistêmico.

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Como otimizar um portfólio de investimentos no Python?

O que são SLMs?

Como calcular retornos históricos de ações no Python?

Como avaliar a relação de risco-retorno de ações no Python

O que são LLMs?

O que são Agentes de IA?

Outros artigos relacionados

Como otimizar um portfólio de investimentos no Python?

Este post apresenta, de forma prática e didática, como aplicar o modelo de otimização de carteiras de Markowitz utilizando Python. A partir de dados reais de ações brasileiras, mostramos como calcular retornos, medir riscos e encontrar a combinação ótima de ativos com base nas preferências de risco do investidor. Utilizamos a biblioteca Riskfolio-Lib para estruturar a análise e gerar gráficos como o conjunto de oportunidades e a fronteira eficiente.

O que são SLMs?

Assim como os LLMs, os Small Language Models (SLMs) são Modelos de Linguagem baseados em IA em versões mais compactas, projetados para funcionar com menos recursos computacionais, menor latência e maior privacidade. Neste exercício mostramos como usar estes modelos usando API's ou localmente através do Python.

Como calcular retornos históricos de ações no Python?

Este artigo tem como objetivo fornecer uma visão abrangente sobre como calcular medidas de retorno histórico e risco no contexto de investimentos e ações, utilizando a linguagem de programação Python como ferramenta.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!