Neste post mostramos como podemos construir um modelo que descreve a Curva IS a partir da linguagem Python. Passamos por todo o processo de construção de um exercício de dados, realizando a coleta, o tratamento, a modelagem e a demonstração dos resultados encontrados.
O objetivo do exercício será estimar uma versão da Curva IS do Modelo Semiestrutural de Pequeno Porte do BCB semelhante a descrita nesse Relatório
(1)
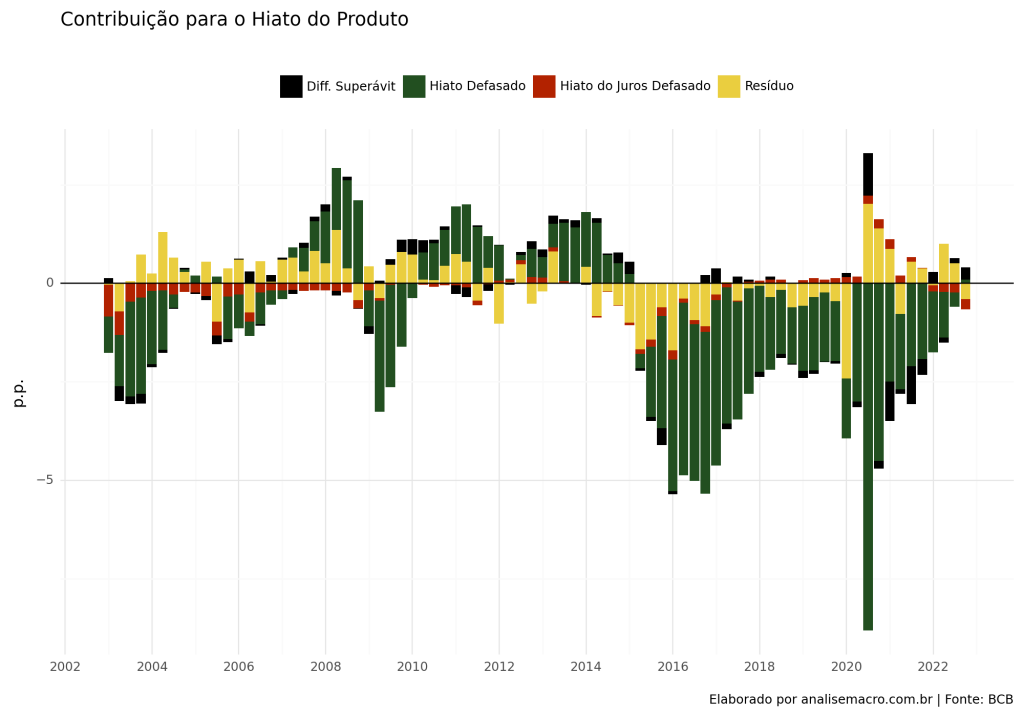
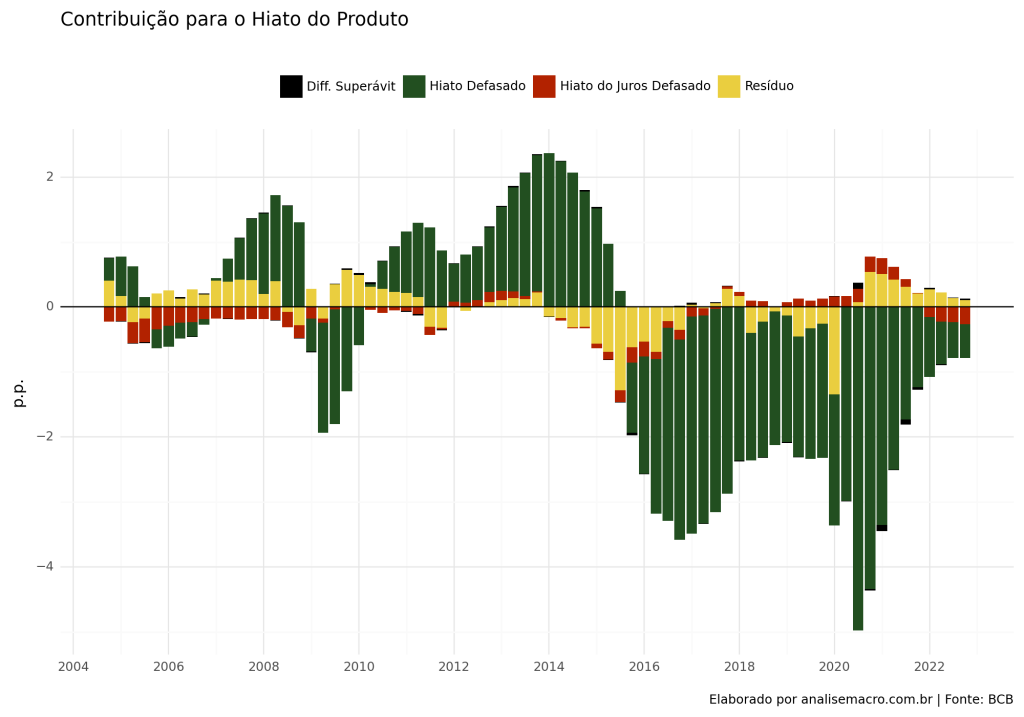
Basicamente, a Curva IS estimada irá descrever a dinâmica do hiato do produto com base em suas próprias defasagens, do hiato do juros real e da variação do superávit primário.
Para construir exercícios Macroeconométricos é necessário aprender as principais ferramentas da linguagem, juntamente com uma série de conhecimentos da área em que se está trabalhando. É para isso que você precisa ser aluno do nosso curso de Macroeconometria usando o Python, que permitirá que você aprenda a realizar análises de diferentes variáveis macroeconômicas.
Dados
O Hiato do produto é aquele construído pelo Banco Central, disponibilizado nos anexos estatísticos do Relatório de Inflação.
O hiato do juros é criado pela diferença entre o juros real ex-ante e o juro neutro, a taxa de juros real obtida pela taxa de juros nominal swap pré-DI de 360 dias deflacionada pela expectativa de inflação relativa ao período de vigência do contrato, o juro de equilíbrio segue uma proxy definida no Relatório de Inflação de dezembro de 2019, dada pela Selic esperada para t+3 deflacionada pela inflação espera para t+3.
A variação do superávit primário utilizada é aquela proveniente do resultado fiscal estrutural construído pela SPE.
Como estimamos a curva IS?
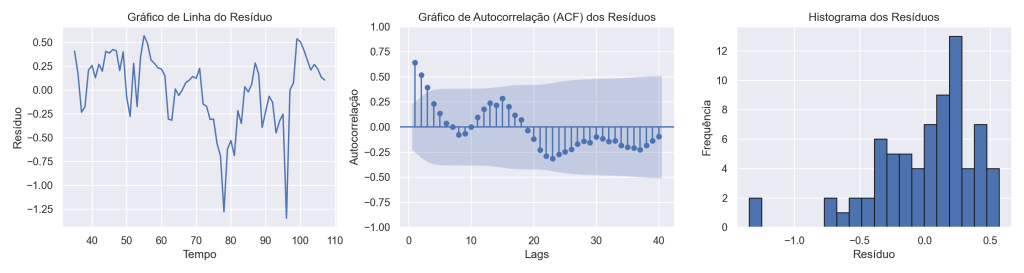
A Curva IS é estimada com base na equação descrita no início usando 2SLS com matriz de covariância robusta para evitar problemas na inferência dos parâmetros causados por autocorrelação e heterocedasticidade nos resíduos. Há também a adição de duas dummies para levar em consideração a crise de 2008 e a pandemia de Covid.
Resultados
A tabela abaixo apresenta os resultados
Código
IV-2SLS Estimation Summary
==============================================================================
Dep. Variable: hiato_bcb R-squared: 0.9563
Estimator: IV-2SLS Adj. R-squared: 0.9531
No. Observations: 73 F-statistic: 7520.8
Date: Wed, Feb 28 2024 P-value (F-stat) 0.0000
Time: 15:08:46 Distribution: chi2(5)
Cov. Estimator: kernel
Parameter Estimates
====================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------------
Intercept 0.1008 0.0776 1.2987 0.1941 -0.0513 0.2530
d_covid -2.4332 0.1623 -14.995 0.0000 -2.7513 -2.1152
d_subprime -1.4406 0.1492 -9.6533 0.0000 -1.7331 -1.1481
hiato_juros_lag1 -0.0770 0.0349 -2.2089 0.0272 -0.1453 -0.0087
hiato_lag1 0.9646 0.0306 31.538 0.0000 0.9047 1.0246
sup_diff_lag1 -0.1822 0.4197 -0.4342 0.6642 -1.0048 0.6404
====================================================================================
Endogenous: hiato_juros_lag1, hiato_lag1, sup_diff_lag1
Instruments: hiato_lag1, juro_real_ex_ante_lag1, neutro_lag2, sup_diff_lag1
Kernel Covariance (HAC)
Debiased: False
Kernel: bartlett
Automatic Bandwidth: True
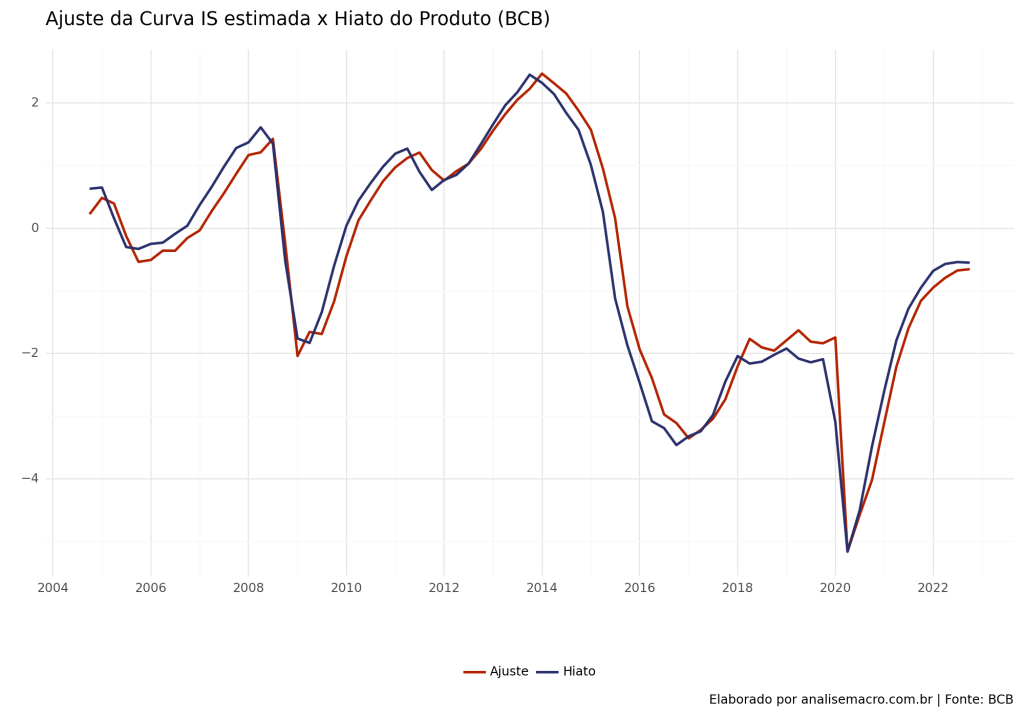
Bandwidth: 3Vemos que houve um bom ajuste na curva estimada conforme o modelo utilizado.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.