Neste exercício, vamos explorar os regimes de volatilidade do mercado acionário brasileiro utilizando o Ibovespa como proxy no Python. Para isso, vamos utilizar a biblioteca yfinance para baixar os dados históricos do índice e a biblioteca statsmodels para ajustar um modelo de regressão dinâmica com mudança de regime (Markov switching).
Markov switching dynamic regression models
Os modelos de regressão dinâmica com mudança de regime (Markov switching) são úteis para analisar séries temporais que apresentam mudanças abruptas no comportamento. Esses modelos assumem que a série temporal é gerada por um processo estocástico que pode mudar de regime ao longo do tempo. A probabilidade de transição entre os regimes é governada por uma cadeia de Markov.
Switching Variance
Uma extensão importante dos modelos de Markov switching é a inclusão de variância de comutação. Isso permite que a variância do processo estocástico seja diferente em cada regime. Essa característica é particularmente útil para analisar séries temporais financeiras, onde a volatilidade pode variar significativamente ao longo do tempo (variância heterocedastica).
Dados
Para este exercício, vamos utilizar os dados semanais do Ibovespa (código ‘^BVSP’) do Yahoo Finance, desde 01/01/2015 até 31/07/2024. Vamos calcular os retornos semanais e utilizar o quadrado dos retornos como variável dependente no modelo de Markov switching.
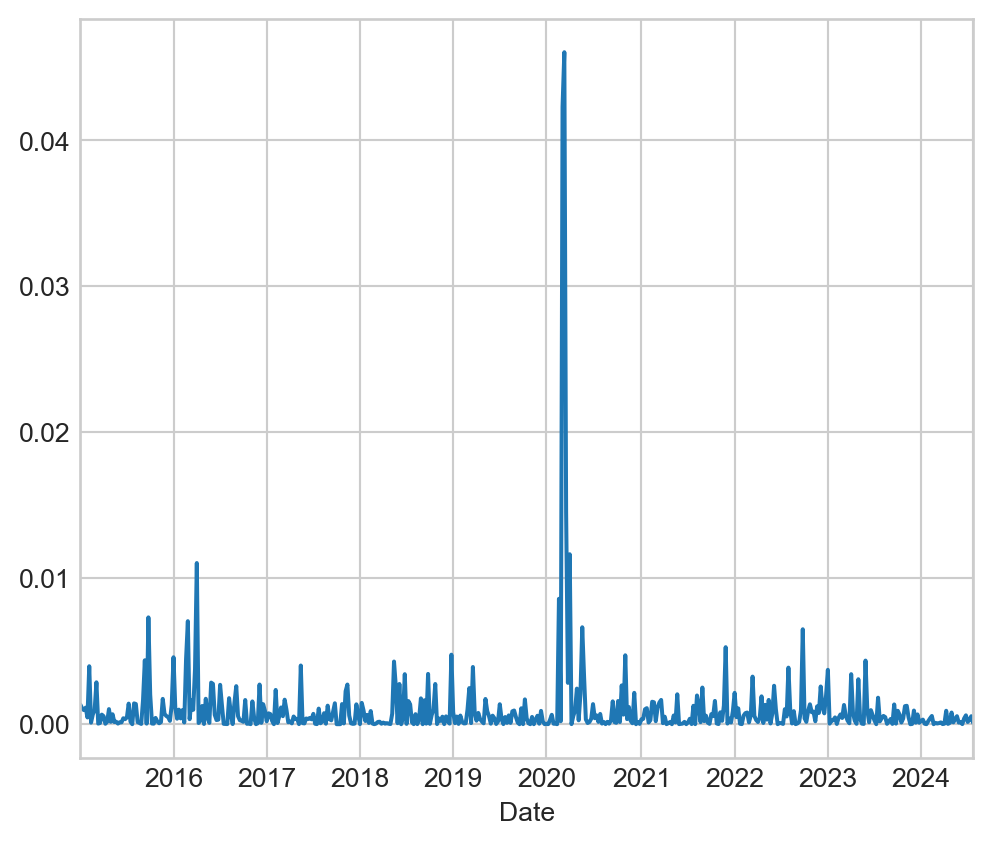
O Gráfico abaixo exibe o comportamento do quadrado dos retornos do Ibovespa ao longo do período amostral.
Na tabela abaixo temos o resultado do MSDR para a variância do índice bovespa. Temos a seguinte leitura:
- Regime 0 (Baixa Variância):
- Constante: 0.0005, estatisticamente significativa (p < 0.001), indicando uma média baixa dos retornos ao quadrado neste regime.
- Coeficiente x1: -0.0202, não estatisticamente significativo (p = 0.129), sugerindo que o impacto desta variável é desprezível neste regime.
- Sigma2 (Variância): 2.219e-07, valor não reportado corretamente.
- Regime 1 (Alta Variância):
- Constante: 0.0034, estatisticamente significativa (p < 0.001), indicando uma média mais alta dos retornos ao quadrado neste regime.
- Coeficiente x1: 0.5448, estatisticamente significativo (p < 0.001), sugerindo um impacto positivo relevante desta variável neste regime.
- Sigma2 (Variância): 3.74e-05, estatisticamente significativa (p < 0.001), indicando uma variância significativamente maior comparada ao Regime 0.
- Parâmetros de Transição de Regime:
- p[0->0]: 0.8833, alta probabilidade de permanecer no Regime 0 (baixa variância).
- p[1->0]: 0.7598, indicando uma probabilidade razoável de transição do Regime 1 para o Regime 0.
O modelo indica que os retornos ao quadrado do índice Bovespa alternam entre dois regimes: um com baixa variância (Regime 0) e outro com alta variância (Regime 1). O regime de alta variância apresenta um impacto positivo significativo da variável x1 e uma maior instabilidade nos retornos. A probabilidade de permanecer no Regime 0 é alta, sugerindo períodos de baixa volatilidade são mais persistentes.
Código
Markov Switching Model Results
==============================================================================
Dep. Variable: returns_sqr No. Observations: 498
Model: MarkovRegression Log Likelihood 2794.155
Date: Thu, 12 Sep 2024 AIC -5572.310
Time: 12:29:32 BIC -5538.625
Sample: 01-15-2015 HQIC -5559.089
- 07-25-2024
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0005 2.68e-05 17.109 0.000 0.000 0.001
x1 -0.0202 0.013 -1.519 0.129 -0.046 0.006
sigma2 2.219e-07 nan nan nan nan nan
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0034 0.001 4.220 0.000 0.002 0.005
x1 0.5448 0.073 7.421 0.000 0.401 0.689
sigma2 3.74e-05 6.77e-06 5.522 0.000 2.41e-05 5.07e-05
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.8833 0.018 48.861 0.000 0.848 0.919
p[1->0] 0.7598 0.058 13.190 0.000 0.647 0.873
==============================================================================
Warnings:
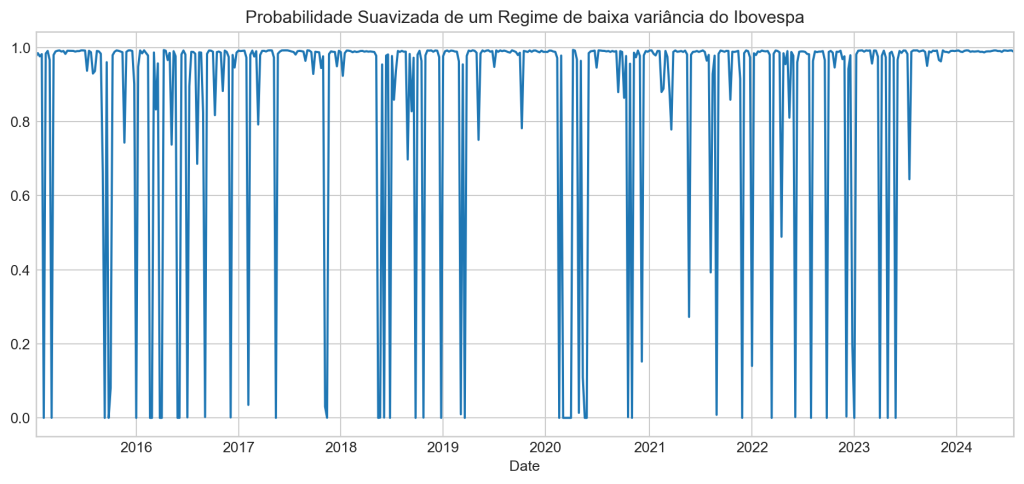
[1] Covariance matrix calculated using numerical (complex-step) differentiation.Por fim, avaliamos a probabilidade de cada regime ao longo do tempo.
Conclusão
O modelo de Markov switching ajustado indica a presença de dois regimes distintos no Ibovespa: um regime de baixa variância e um regime de alta variância. O regime de alta variância apresenta um impacto positivo significativo da variável exógena (retornos defasados) e uma maior instabilidade nos retornos. A probabilidade de permanecer no regime de baixa variância é alta, sugerindo que períodos de baixa volatilidade são mais persistentes.
A análise da probabilidade suavizada de cada regime ao longo do tempo mostra que o Ibovespa passou por períodos de alta e baixa volatilidade durante o período analisado.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, fale com a gente no Whatsapp e veja como fazer parte do Clube AM, clicando aqui.