Introdução
Os Modelos de Componentes Não Observados (UC) permitem decompor uma série temporal em diferentes componentes, como tendência, ciclo, sazonalidade e ruído. Esses modelos são flexíveis e permitem que os componentes evoluam estocasticamente, o que os torna adequados para capturar dinâmicas econômicas. Neste exercício, utilizamos a Taxa de Desocupação Brasileira e comparamos os resultados do UC com o Filtro HP, um método mais tradicional.
O procedimento de coleta, tratamento, modelagem e avaliação dos modelos são todos realizados usando Python, por meio das bibliotecas pandas, matplotlib e statsmodels.
Dados
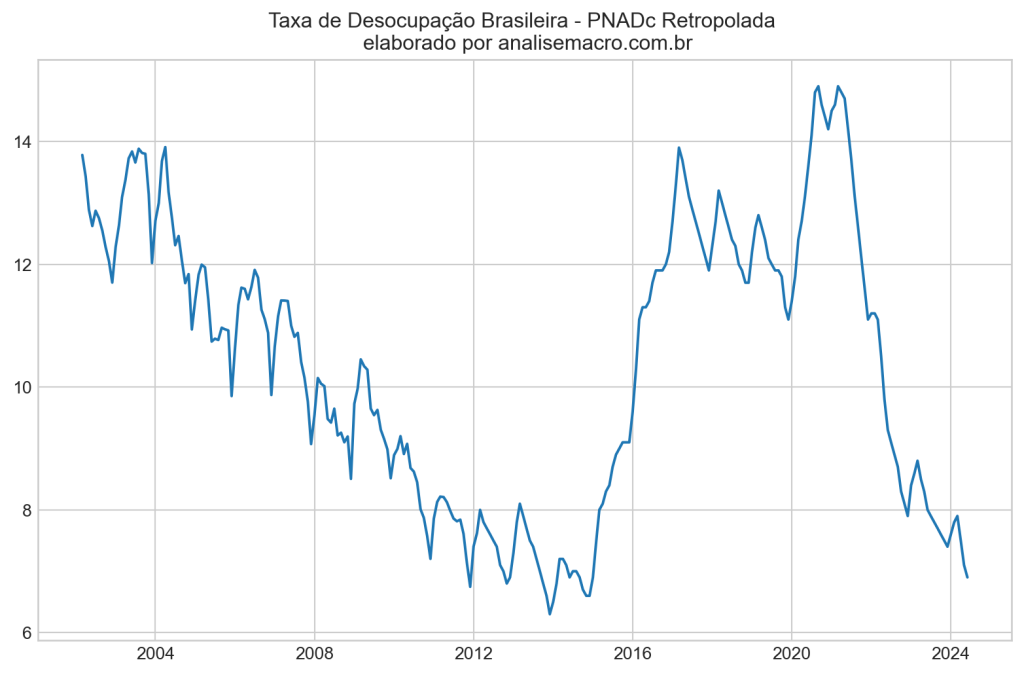
Usamos a Taxa de Desocupação Brasileira Retropolada, com dados de março de 2002 a junho de 2024. Esses dados foram obtidos através da retropolação da série de desemprego, permitindo uma análise mais longa e detalhada da série histórica. Para saber mais sobre como foi obtido a série, veja o exercício Retropolando a série do desemprego no Brasil, disponível no Clube AM e no curso Macroeconometria usando Python.
Modelagem
Filtro HP
O Filtro de Hodrick-Prescott (HP) é utilizado para suavizar séries temporais e separar os componentes de ciclo e tendência. Ele aplica uma penalização à variabilidade da tendência, produzindo uma série suavizada. Nesta análise, o HP foi utilizado para extrair a tendência da Taxa de Desocupação Brasileira, e os resultados serão comparados com os obtidos pelo MCNO.
Modelo de Componentes Não Observados (UC)
O Modelo de Componentes Não Observados (UC) utilizado neste exercício inclui uma tendência aleatória, um componente cíclico estocástico amortecido e um componente sazonal com periodicidade de 12 meses. A especificação do modelo captura:
- Uma tendência estocástica que evolui ao longo do tempo, sem um padrão fixo.
- Um ciclo estocástico amortecido, que reflete flutuações cíclicas na economia e diminui sua intensidade ao longo do tempo.
- Um componente sazonal que reflete variações anuais recorrentes, comuns em séries temporais como a taxa de desemprego.
Esses componentes permitem que o modelo MCNO capture de maneira mais flexível as variações na série de desemprego. A comparação com o Filtro HP revela diferenças na forma como cada método aborda a decomposição dos componentes, destacando as vantagens do modelo UC em capturar dinâmicas econômicas complexas.
Coleta de dados
O código em Python completo deste exercício está disponível para os membros do Clube AM.
Unobserved components with stochastic cycle (UC)
Realizamos o ajuste do modelo UC. Os resultados, bem como a especificação pode ser conferida na tabela abaixo.
Para aqueles que desejam saber como foi criado o resultado abaixo usando o Python, o código está disponível para os membros do Clube AM .
Unobserved Components Results
=====================================================================================
Dep. Variable: pnad No. Observations: 268
Model: random trend Log Likelihood 5.351
+ stochastic seasonal(12) AIC -0.702
+ damped stochastic cycle BIC 16.965
Date: Fri, 20 Sep 2024 HQIC 6.406
Time: 10:51:25
Sample: 03-01-2002
- 06-01-2024
Covariance Type: opg
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
sigma2.trend 0.0004 0.000 1.387 0.166 -0.000 0.001
sigma2.seasonal 0.0003 0.000 2.084 0.037 2.08e-05 0.001
sigma2.cycle 0.0320 0.003 9.622 0.000 0.025 0.039
frequency.cycle 0.1478 0.017 8.623 0.000 0.114 0.181
damping.cycle 0.9725 0.011 88.082 0.000 0.951 0.994
===================================================================================
Ljung-Box (L1) (Q): 2.90 Jarque-Bera (JB): 5.34
Prob(Q): 0.09 Prob(JB): 0.07
Heteroskedasticity (H): 0.47 Skew: 0.31
Prob(H) (two-sided): 0.00 Kurtosis: 3.35
===================================================================================Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Temos a seguinte leitura da tabela acima: Componente de Tendência Aleatória (Random Trend): O modelo captura a tendência de longo prazo da série de desocupação. O parâmetro σ²trend está relacionado à variabilidade da tendência:
- σ²trend=0.0004: A variância da tendência é baixa, indicando que a tendência da taxa de desemprego varia de forma suave e estável ao longo do tempo.
- P-valor = 0.165: Como o p-valor está acima de 0.05, a variação estocástica na tendência não é significativa, sugerindo que a tendência de longo prazo da desocupação é relativamente estável.
Componente Sazonal Estocástico (Stochastic Seasonal):
A sazonalidade reflete flutuações recorrentes na série de desemprego, comuns em dados econômicos.
- σ²seasonal=0.0003: A variância sazonal é baixa, o que indica que as variações sazonais são pequenas, mas ainda presentes.
- P-valor = 0.037: O componente sazonal é significativo (p-valor < 0.05), o que sugere que as variações sazonais, como a demanda sazonal por emprego, afetam a taxa de desocupação de maneira importante.
Componente Cíclico Estocástico Atenuado (Damped Stochastic Cycle):
Este componente captura ciclos econômicos, como períodos de recessão ou crescimento.
- σ²cycle=0.0320: A variância do componente cíclico é relativamente alta, o que sugere que os ciclos econômicos têm um impacto substancial na série de desemprego.
- Frequência do ciclo (frequency.cycle) = 0.1478: Esse valor indica ciclos de aproximadamente 3.5 anos (42.5 períodos). Isso é consistente com ciclos econômicos de médio prazo, que afetam a taxa de desocupação.
- Damping (damping.cycle) = 0.9725: O ciclo é atenuado lentamente (coeficiente próximo de 1), sugerindo que os ciclos econômicos têm impactos persistentes na taxa de desemprego ao longo do tempo.
- P-valor < 0.001: Tanto a variância, a frequência e o amortecimento do ciclo são altamente significativos, mostrando que o componente cíclico desempenha um papel crucial na série.
Diagnósticos do Modelo:
- Ljung-Box (L1) (Q) = 2.91, Prob(Q) = 0.09: O teste Ljung-Box sugere que não há autocorrelação significativa nos resíduos, indicando que o modelo captura bem a estrutura da série temporal.
- Jarque-Bera (JB) = 5.34, Prob(JB) = 0.07: O teste Jarque-Bera mostra que os resíduos estão próximos de uma distribuição normal (p-valor próximo de 0.07), com pouca assimetria ou curtose.
- Heterocedasticidade (H) = 0.47, Prob(H) = 0.00: O teste indica a presença de heterocedasticidade (p-valor < 0.05), sugerindo que a variância dos resíduos varia ao longo do tempo, o que pode exigir ajustes adicionais no modelo para lidar com essa volatilidade variável.
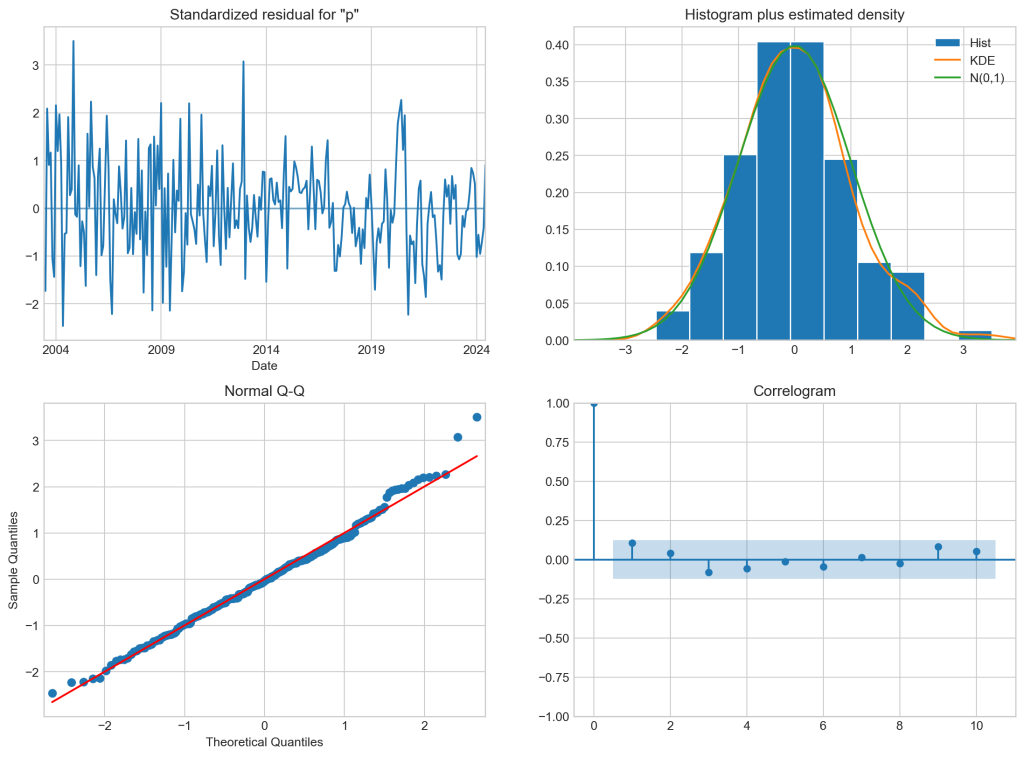
A figura abaixo exibe os gráficos de diagnóstico do modelo, reiterando os resultados dos testes estatísticos: resíduos heterocedásticos, normalmente distribuídos e com ausência de autocorrelação.
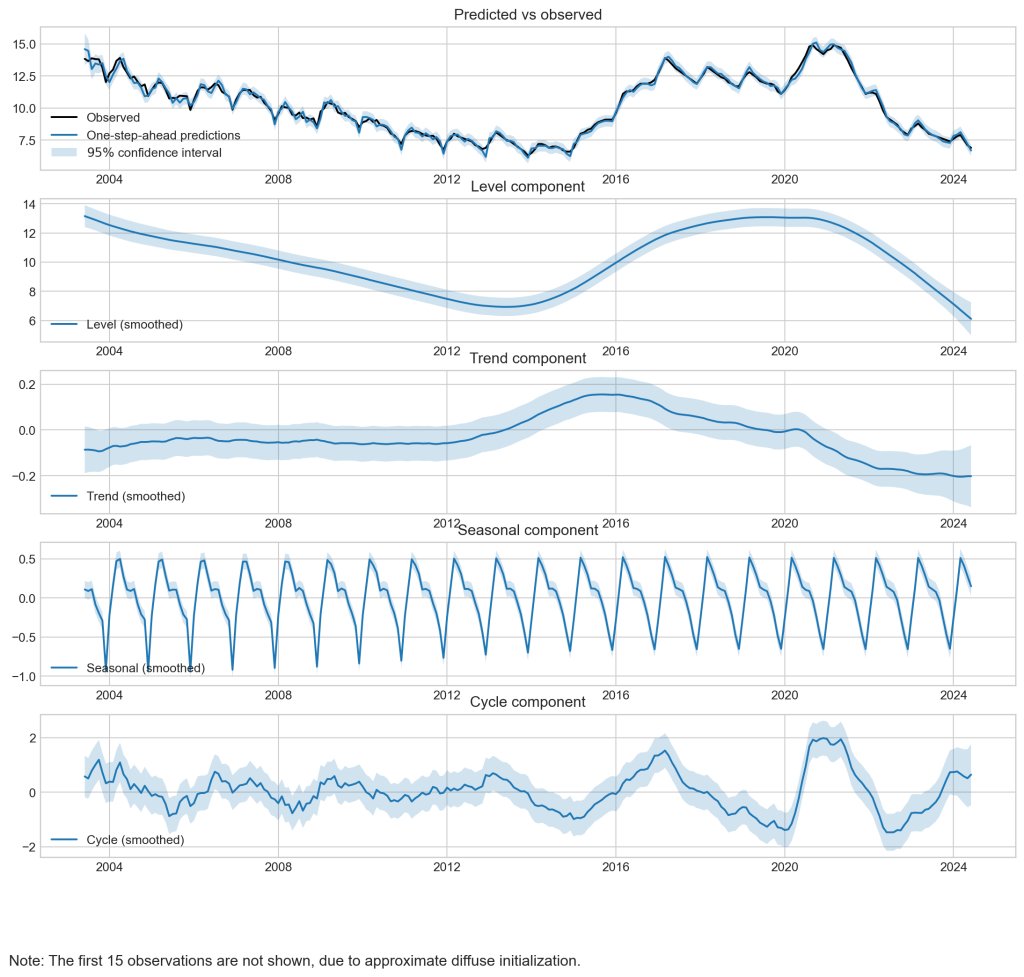
O gráfico abaixo apresenta os componentes do modelo de componentes não observados (UC) aplicados à taxa de desocupação brasileira. Aqui está uma análise resumida:
- Predicted vs Observed: As previsões do modelo seguem de perto a série observada, com uma margem de confiança de 95%, mostrando uma boa aderência do modelo.
- Level Component: A tendência de longo prazo indica uma queda suave na taxa de desocupação até 2014, com um aumento até 2020, seguido de nova queda.
- Trend Component: O componente de tendência exibe um padrão suave e crescente até 2020, com posterior declínio, capturando a dinâmica de longo prazo.
- Seasonal Component: A sazonalidade é constante ao longo do tempo, refletindo flutuações anuais regulares, comuns em dados de emprego.
- Cycle Component: O componente cíclico mostra variações econômicas de médio prazo, com intensificação em períodos de crise econômica (2008 e 2020).
Em resumo, o modelo UC captura bem a estrutura temporal da série, identificando uma tendência suave, sazonalidade estável e ciclos econômicos.
Comparação: Filtro HP e UC
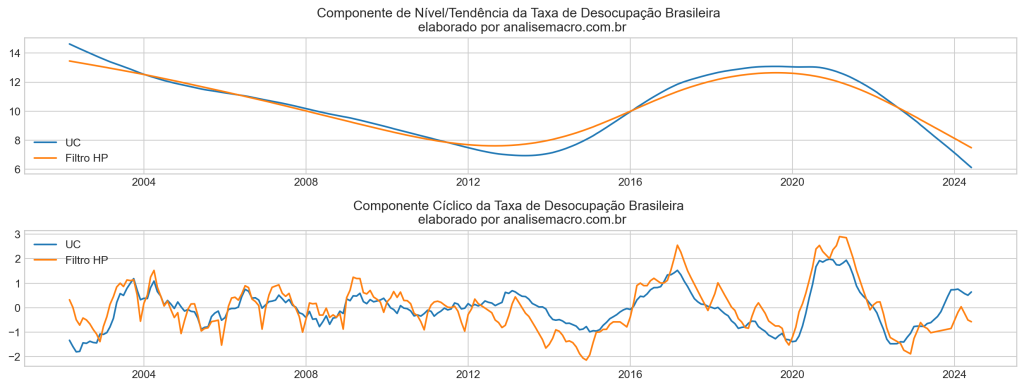
A análise dos gráficos revela a comparação entre os componentes extraídos pelo Modelo de Componentes Não Observados (UC) e pelo Filtro HP para a Taxa de Desocupação Brasileira.
Componente de Nível/Tendência:
No gráfico superior, a tendência de longo prazo é capturada tanto pelo UC quanto pelo Filtro HP. Observamos que:
- UC mostra uma tendência mais suave e prolongada, capturando melhor as flutuações de longo prazo, com uma leve desaceleração a partir de 2015 e uma queda acentuada em 2024, chegando ao valor de 6,1% em jun/2024.
- Filtro HP segue um padrão semelhante, mas parece mais linear e menos sensível a mudanças de médio prazo, especialmente no final do período, chegando ao valor de 7,4% em jun/2024.
Componente Cíclico:
No gráfico inferior, o componente cíclico captura as variações de curto e médio prazo:
- UC apresenta flutuações cíclicas mais suaves e regulares ao longo do tempo, com variações menos acentuadas.
- Filtro HP tem oscilações mais intensas e voláteis, capturando ciclos de forma mais abrupta, especialmente durante a crise de 2015-2016 e o período pós-2020. Um ponto importante é que o Ciclo do Filtro HP captura a sazonalidade, diferente do UC.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, fale com a gente no Whatsapp e veja como fazer parte do Clube AM, clicando aqui.