Na terça-feira recebi um e-mail da jornalista Gabriela David, da revista Bons Negócios, me fazendo algumas perguntas sobre as perspectivas para o setor de alimentação fora de casa. A Gabriela estava interessada em food trucks, aqueles pequenos caminhões que servem comida nas ruas de Nova York e que viraram moda na cidade de São Paulo. Será que é uma febre passageira ou deve virar tendência nas principais cidades do país, questiona Gabriela. Ademais, quais são as perspectivas para esse negócio, diante dos problemas na economia brasileira, pergunta a jornalista. Para ajudar Gabriela, devemos saber, em primeiro lugar, que alimentação fora de casa é um negócio que depende diretamente do comportamento da renda das famílias. Isto porque, ainda que as pessoas usem cartão de crédito para pagar restaurantes, pensões e food trucks, não faz muito sentido pensar que as pessoas se endividam para comer fora de casa, não é mesmo? No máximo, paga-se o cartão no próximo mês, logo é preciso que a renda esteja crescendo ao longo do tempo para que negócios como esse sejam objeto de expansão. Dito isto, vamos aos dados?
Bom, dado que renda das famílias é fundamental para negócios como food trucks, devemos nos perguntar como ela deve se comportar nos próximos meses e anos, não é mesmo? Para isso, precisamos saber do que depende a renda. Uma primeira pista é identificar o comportamento do crescimento da economia. Isto porque, se o PIB cresce ao longo do tempo, é razoável supor que a renda das famílias também tende a crescer. Isto porque, maior crescimento da economia implica em maior absorção de mão de obra ou menor desemprego. Este, por sua vez, faz aumentar o poder de barganha dos indivíduos, o que leva a maior crescimento dos salários e, portanto, da renda das famílias.
Tudo bem intuitivo, não é mesmo? Pois é, vamos melhorar isso, então? Vamos fazer um exercício simples no R que consiste basicamente em ver se o desemprego ajuda a prever o que irá ocorrer com a renda. Isso pode ser feito via o famoso teste de causalidade de granger, que no R pode ser acessado via o carregamento do pacote vars. Desse modo, se chegarmos à conclusão que, de fato, o desemprego ajuda a prever a renda das famílias [auferida, principalmente, por meio de salários], podemos ter alguma noção do que ocorrerá no futuro.
Para começar o exercício, precisamos, claro, de dados. Montei meu excel com quatro séries, com observações de março de 2003 a março de 2015: crescimento interanual da renda nominal, crescimento interanual da renda real, desemprego como % da PEA e desemprego dessazonalizado também como % da PEA. As três primeiras foram retiradas da Pesquisa Mensal de Emprego (PME), do SIDRA, o banco de dados on-line do IBGE, enquanto a última é derivada da série original de desemprego com a aplicação do X12-Arima, no Gretl. Podemos, assim, começar dando uma olhada nos gráficos das séries com a função gtsplot, do pacote BMR. Essa função tem sido recorrentemente utilizada aqui, mas como diria Machado de Assis, é preciso incutir conceitos na mente do leitor por meio de repetição, não é mesmo? Abaixo o código e os gráficos.
############### GRÁFICOS DAS SERIES #######################
data.part <- window(data, start=c(2011,1))
dates <- seq(as.Date('2011-01-01'), as.Date('2015-03-01'), by='1 month')
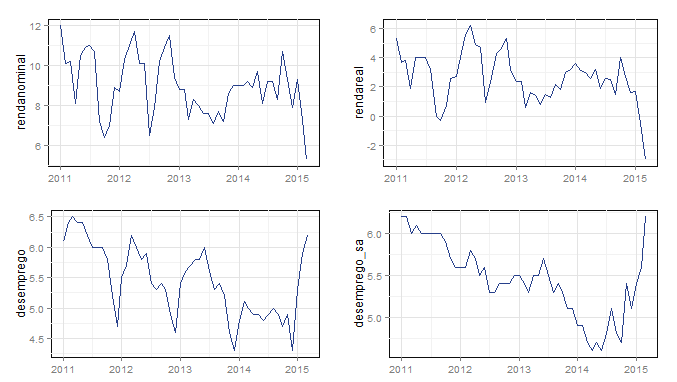
gtsplot(data.part, dates=dates)
Observe que apenas com esses quatro gráficos já é possível verificar o que está acontecendo na economia brasileira. Veja que o desemprego está aumentando nos últimos meses, enquanto o crescimento da renda [real e nominal] interanual tem caído. Isso já é um bom início de conversa para o que a Gabriela quer, não é mesmo? Mas, vamos em frente.
Antes de chegarmos ao teste de granger, vamos dar uma olhada em algumas correlações. Com a função cor aplicada sobre o seu objeto no R, você pode obter uma tabela com as correlações entre todas as séries, como abaixo, usando o pacote stargazer.
| rendanominal | rendareal | desemprego | desemprego_sa | |
| rendanominal | 1 | 0,82 | -0,63 | -0,64 |
| rendareal | 0,82 | 1 | -0,56 | -0,56 |
| desemprego | -0,63 | -0,56 | 1 | 0,98 |
| desemprego_sa | -0,64 | -0,56 | 0,98 | 1 |
Como esperado, renda e desemprego apresentam uma relação bastante razoável. Como dissemos acima, entretanto, a relação entre eles envolve alguma defasagem. Desse modo, podemos ver a correlação cruzada para nos decidirmos sobre quais variáveis específicas vamos fazer o teste de granger. Mostro abaixo, apenas, os gráficos entre renda nominal e desemprego sem ajustes sazonais. Foi usada a função lag2.plot do pacote astsa.
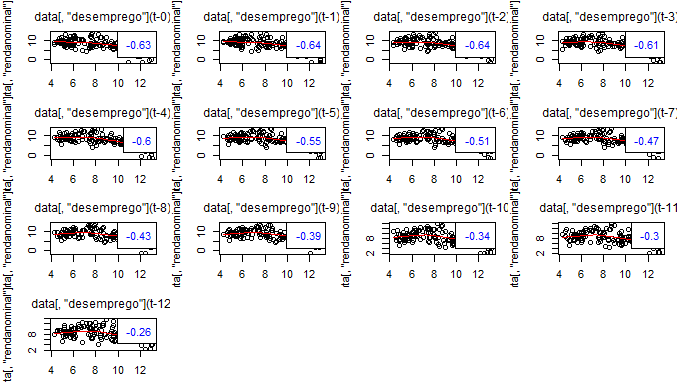
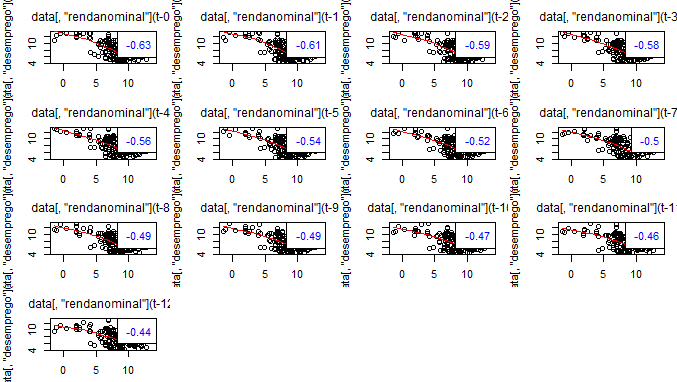
Bom, com esses gráficos é possível ver que a correlação [negativa] se torna mais forte quando a renda nominal é confrontada com a primeira e segunda defasagens do desemprego sem ajustes sazonais. Temos, assim, nossos candidatos para o granger. Isto é, vamos verificar se a correlação entre renda nominal e desemprego sem ajustes implica em causalidade, no sentido dado pelo teste. Antes, claro, temos que verificar se essas séries são estacionárias, não é mesmo? Para isso, vamos aplicar o protocolo de Pfaff (2008) e utilizar o pacote urca para o teste ADF Sequencial ilustrado pelo autor.
Um detalhe chato [para alguns] é que na hora de rodar o teste ADF é preciso escolher o número de defasagens, de modo a não incorrer em autocorrelação serial. Em geral, se faz essa escolha através de critérios de informação. Aqui, entretanto, vamos aplicar o teste Ljung-Box aos resíduos do teste ADF para verificar se o lag utilizado incorre em autocorrelação. Isso, claro, seria muito chato se tivéssemos de fazer um por um. O Ricardo Lima, entretanto, me passou uma função e um loop utilizados no curso de mestrado dele, no curso de séries temporais, lá na Universidade de Estocolmo. A ideia da função e do loop é aplicar o teste Ljung-Box sobre os resíduos do teste ADF e gerar uma sequência de gráficos no ambiente do RStudio de forma a verificar sobre qual lag não há autocorrelação [caso tenha interesse na função e no loop, entre em contato]. No nosso caso, os gráficos do desemprego e da renda nominal com os lags adequados são postos abaixo.
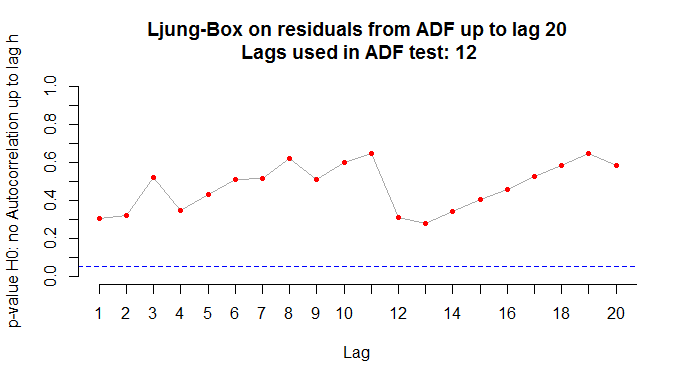
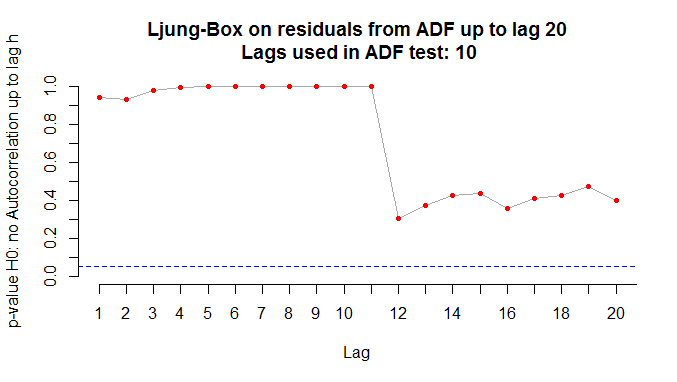
Com 12 e 10 lags, respectivamente, para o desemprego e renda, podemos garantir que não há autocorrelação na hora de rodar a equação do teste ADF. Com isto, podemos agora rodar a função ur.df do pacote urca para definir o processo gerador das séries. De modo a comparar a estatística de teste com os valores críticos, vamos rodar o código abaixo, pegando apenas esses dados. A partir disso, montamos uma tabela com a função stargazer do pacote de mesmo nome.
######### Teste Pfaff (2008) para Desemprego ########### lags.adf <- 12 ### Lag escolhido com o Ljung-Box data.ct <- ur.df(data[,'desemprego'], type='trend' , lags=lags.adf)@teststat data.ct.cval <- t(ur.df(data[,'desemprego'], type='trend' , lags=lags.adf)@cval) ur.ct <- round(rbind(data.ct, data.ct.cval), digits=2) table.data.ct <- stargazer(ur.ct, title='Teste ADF com tendência e drift', type='html', out='adf1.html', decimal.mark=',', digits=2, align=T)
| tau3 | phi2 | phi3 | |
| statistic | -3,24 | 5,87 | 7,60 |
| 1pct | -3,99 | 6,22 | 8,43 |
| 5pct | -3,43 | 4,75 | 6,49 |
| 10pct | -3,13 | 4,07 | 5,47 |
A tabela nos indica que a 5% não é possível rejeitar a hipótese nula [que a série tem raiz unitária]. Essa informação é obtida ao compararmos a estatística de teste [-3,24] com o valor crítico da estatística tau3 [-3,43]: se for maior em módulo, rejeita-se. O protocolo que estamos usando, Pfaff (2008), nos indica que devemos consultar a estatística phi3, cuja hipótese nula é que o coeficiente da tendência é igual a zero, dado que é igual a zero. Ao fazer isso, nós rejeitamos H0, a 5%. O protocolo manda, então, ver se
é igual a zero pela tabela normal. É possível ver os coeficientes com o mesmo comando acima, apenas modificando a parte final por @testreg$coefficients ou rodar a função ur.df sem especificar parâmetros e visualizar todos os dados com a função summary. Abaixo, coloco os coeficientes, com os respectivos p-valores.
| Estimate | Std. Error | t value | Pr(> | t| ) | |
| (Intercept) | 2,87 | 0,96 | 3,00 | 0,003 |
| z.lag.1 | -0,25 | 0,08 | -3,24 | 0,002 |
| tt | -0,01 | 0,004 | -2,80 | 0,01 |
| z.diff.lag1 | 0,12 | 0,10 | 1,23 | 0,22 |
| z.diff.lag2 | 0,09 | 0,10 | 0,96 | 0,34 |
| z.diff.lag3 | 0,08 | 0,09 | 0,83 | 0,41 |
| z.diff.lag4 | 0,05 | 0,09 | 0,53 | 0,59 |
| z.diff.lag5 | 0,02 | 0,09 | 0,19 | 0,85 |
| z.diff.lag6 | 0,08 | 0,08 | 0,98 | 0,33 |
| z.diff.lag7 | 0,04 | 0,08 | 0,46 | 0,64 |
| z.diff.lag8 | -0,02 | 0,08 | -0,21 | 0,83 |
| z.diff.lag9 | -0,03 | 0,08 | -0,40 | 0,69 |
| z.diff.lag10 | 0,01 | 0,07 | 0,09 | 0,93 |
| z.diff.lag11 | 0,01 | 0,07 | 0,12 | 0,90 |
| z.diff.lag12 | 0,58 | 0,07 | 8,22 | 0 |
Estamos interessados no z.lag.1, que é estatisticamente significativo pela tabela normal. Logo, podemos dizer que o desemprego é estacionário ao redor de uma tendência e tratá-lo dessa forma na hora de rodar o teste de granger. Simples, não? Não, eu sei. Mas, aos poucos, você se acostuma e as coisas passam a ser mais naturais.
Fiz o mesmo procedimento para a renda e cheguei à conclusão que ela é estacionária. Assim, com ambas as séries estacionárias, podemos, enfim, rodar o teste de granger. Isso é feito com o código abaixo, a partir do carregamento do pacote vars.
####################### GRANGER CAUSALITY ###########################
granger <- cbind(data[,'rendanominal'],data[,'desemprego'])
colnames(granger) <- c('renda', 'desemprego')
VARselect(granger,lag.max=12, type=c("const"),season=NULL)
grangertest(granger[,'renda']~granger[,'desemprego'],
order=1, data=granger)
grangertest(granger[,'desemprego']~granger[,'renda'],
order=1, data=granger)
E abaixo os resultados...
> grangertest(granger[,'renda']~granger[,'desemprego'], + order=1, data=granger) Granger causality test Model 1: granger[, "renda"] ~ Lags(granger[, "renda"], 1:1) + Lags(granger[, "desemprego"], 1:1) Model 2: granger[, "renda"] ~ Lags(granger[, "renda"], 1:1) Res.Df Df F Pr(>F) 1 141 2 142 -1 10.179 0.001751 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 > grangertest(granger[,'desemprego']~granger[,'renda'], + order=1, data=granger) Granger causality test Model 1: granger[, "desemprego"] ~ Lags(granger[, "desemprego"], 1:1) + Lags(granger[, "renda"], 1:1) Model 2: granger[, "desemprego"] ~ Lags(granger[, "desemprego"], 1:1) Res.Df Df F Pr(>F) 1 141 2 142 -1 0.1978 0.6572
Então, leitor, chegamos onde queríamos. Recapitulando, queríamos verificar se o desemprego ajuda a prever o comportamento da renda nominal. De fato, o teste de granger não nos impede de fazermos essa afirmação. O resultado do teste mostra que o desemprego granger causa a renda, dada a rejeição da hipótese nula. Para o caso contrário, entretanto, não podemos rejeitar a hipótese nula de que a renda não granger causa o desemprego. Desse modo, podemos nos concentrar no argumento de que o comportamento do desemprego é um bom indicador para prevermos a renda.
Se é assim, o aumento do desemprego em 2015, como escrevi em post recente, deve contaminar a renda nominal. Dada a elevada inflação, a renda real deve, portanto, sofrer pelos dois lados, o que compromete negócios que têm nela um de seus determinantes de expansão. Em outras palavras, como disse para a Gabriela, os empreendedores devem ter cautela. É uma boa oportunidade de negócio, sem dúvida, mas no curto prazo, creio que é um tanto quanto arriscado fazer pesados investimentos, dado que o cenário prospectivo não é dos melhores.
Um outro aspecto que ela me perguntou foi sobre o impacto regional desse tipo de empreendimento. Minha resposta foi que depende muito de como as prefeituras e os empreendedores encaram o negócio. Observo que há grandes possibilidades de geração de uma rede de trucks, com feiras ou algo do tipo, o que exige infraestrutura (praças, recolhimento de lixo, segurança, etc.), bem como coordenação dos empreendedores. Se assim for feito, sim, acho que pode ter impacto, dado que gera externalidades positivas, com a geração de outros negócios ao redor (parques de diversão, artesanato, festivais de música, etc.).
No mais, leitor, espero que esse exercício tenha dado uma pequena amostra de como os economistas trabalham e como uma análise de conjuntura pode ser feita, com algum rigor, além de apenas chutes e pontapéis... 🙂