Modelos de previsão macroeconômica podem facilmente alcançar um número elevado de variáveis. Mesmo modelos simplificados, como o Modelo de Pequeno Porte (MPP) do Banco Central, usam cerca de 30 variáveis. Isso impõe um grande desafio ao nosso dia a dia: como fazer a gestão destes dados para uso em modelos, desde a coleta até o tratamento?
Neste artigo mostramos como é possível automatizar, usando linguagem de programação, todo o processo de preparação de dados para uso em modelos preditivos macroeconômicos. Tomando como exemplo as variáveis do MPP, mostramos como coletar e tratar os dados de diferentes fontes e, no fim, montamos uma tabela que serve de base para a estimação do modelo.
Etapa 1: identificar as variáveis
Partindo de um modelo macroeconômico a ser estimado, o primeiro passo é identificar quais são as variáveis necessárias para o mesmo. No caso do MPP, as variáveis estão descritas no relatório de inflação publicado pelo Banco Central.
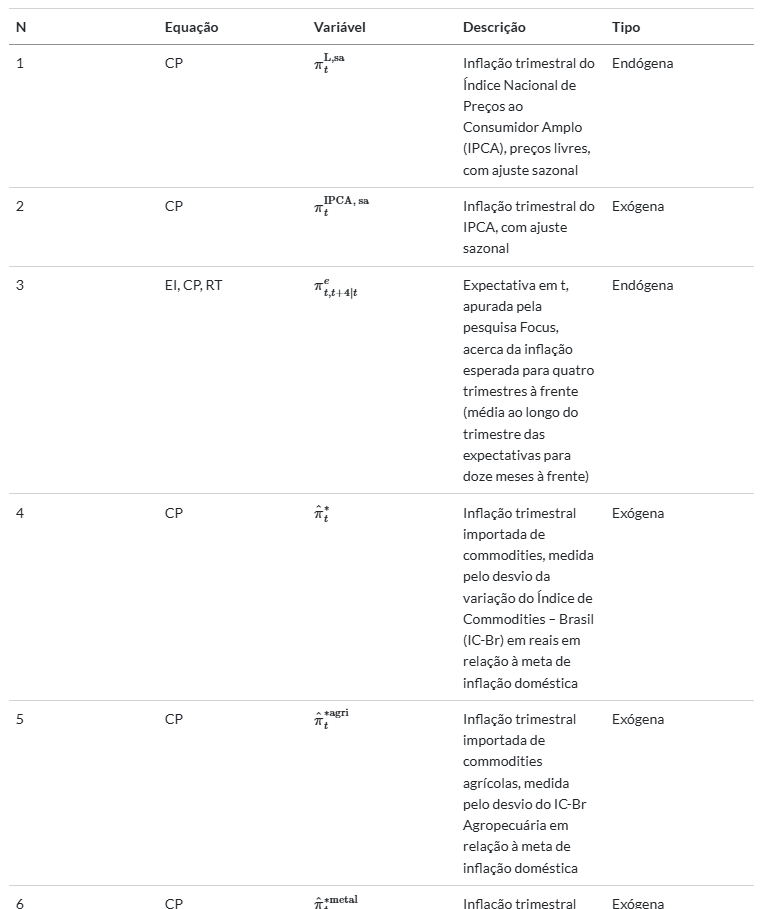
Para facilitar a gestão de informações, o usuário pode montar uma tabela resumo destas variáveis, contendo as principais informações, como no exemplo abaixo:
Etapa 2: coletar os dados
Em seguida, devemos identificar as fontes de dados que dão origem a estas variáveis e coletar os dados brutos. No caso do MPP, alguns dados não estão disponíveis de forma fácil ou pública, então adaptações ou cortes podem ser necessários.
Em suma, é necessário coletar dados destas fontes para o exemplo em questão:
- Banco Central do Brasil (BCB)
- Instituto Brasileiro de Geografia e Estatística (IBGE)
- National Oceanic and Atmospheric Administration (NOAA)
No caso do BCB, os dados podem vir de mais de uma fonte: Sistema Gerenciador de Séries Temporais, Sistema de Expectativas, API Documentos do Copom e outras APIs espalhadas pelo site da instituição.
Através da linguagem R e do pacote rbcb coletamos a maioria destes dados.
No caso do IBGE, todas as tabelas de dados necessárias estão localizadas no sistema SIDRA e podemos usar o pacote sidrar para fazer a coleta dos dados.
Por fim, no caso do NOAA, a variável ONI é disponibilizada através de uma URL para um arquivo de texto. Utilizamos o pacote readr para coletar estes dados.
Etapa 3: tratar dados e criar variáveis
Nesta etapa o objetivo é construir uma tabela final que servirá de base para o modelo, contendo todas as variáveis necessárias. Os dados coletados chegam em variados formatos, nem sempre sendo o tabular. Dessa forma, devemos tratar as informações de forma que representamos os dados na unidade de medida apropriada para o modelo e em formato tabular.
No caso do MPP, devemos converter os dados de modo a obter as variáveis em frequência trimestral e em semelhante unidade de medida descrita pelo BCB (não é possível replicar as variáveis usadas pela instituição pois o código fonte não é aberto pela mesma). Ademais, algumas variáveis são não observáveis e precisam ser estimadas e outras precisam ser calculadas.
A seguir apresentamos as tabelas individuais para as variáveis do MPP, sendo que algumas variáveis do modelo original não estão presentes por dificuldade de acesso/disponibilização de dados públicos ou por terem sido arbitrariamente excluídas.
- Expectativa de inflação acumulada quatro trimestres à frente consistente com o modelo (model-consistent expectations)
| date | ipca_expec |
|---|---|
| 2001-10-01 | 4.70 |
| 2002-01-01 | 4.81 |
| 2002-04-01 | 4.53 |
| 2002-07-01 | 5.64 |
| 2002-10-01 | 12.26 |
| 2003-01-01 | 9.30 |
- Inflação trimestral do Índice Nacional de Preços ao Consumidor Amplo (IPCA), preços livres, com ajuste sazonal
| date | ipca_livres | ipca_livres_sa |
|---|---|---|
| 1999-07-01 | 2.5915500 | 2.1291681 |
| 1999-10-01 | 0.4902232 | 0.7818590 |
| 2000-01-01 | 0.5710226 | 1.0762945 |
| 2000-04-01 | 2.5903025 | 2.2557722 |
| 2000-07-01 | 0.7604714 | 0.2981345 |
| 2000-10-01 | 0.7107491 | 1.0023230 |
- Inflação trimestral do IPCA, com ajuste sazonal
| date | ipca | ipca_sa |
|---|---|---|
| 1999-07-01 | 2.88 | 2.5162687 |
| 1999-10-01 | 1.05 | 1.3691481 |
| 2000-01-01 | 1.97 | 2.3843835 |
| 2000-04-01 | 2.76 | 2.3901643 |
| 2000-07-01 | 0.97 | 0.6063608 |
| 2000-10-01 | 0.66 | 0.9792566 |
- Inflação trimestral importada de commodities, medida pelo desvio da variação do Índice de Commodities – Brasil (IC-Br) em reais em relação à meta de inflação doméstica
- Inflação trimestral importada de commodities agrícolas, medida pelo desvio do IC-Br Agropecuária em relação à meta de inflação doméstica
- Inflação trimestral importada de commodities metálicas, medida pelo desvio do IC-Br Metal em relação à meta de inflação doméstica
- Inflação trimestral importada de commodities energéticas, medida pelo desvio do IC-Br Energia em relação à meta de inflação doméstica
| date | ic_br | ic_br_agro | ic_br_energia | ic_br_metal |
|---|---|---|---|---|
| 1999-01-01 | 39.904707 | 36.4659724 | 60.973747 | 47.028129 |
| 1999-04-01 | -16.053561 | -17.1533948 | -12.872881 | -11.606260 |
| 1999-07-01 | 2.151963 | -0.5632035 | 11.376392 | 9.623529 |
| 1999-10-01 | -8.613144 | -8.2748196 | -12.850746 | -7.579916 |
| 2000-01-01 | -10.549836 | -11.0637272 | -5.542484 | -11.278885 |
| 2000-04-01 | 2.159968 | 2.5087083 | 11.534157 | -5.411146 |
- Desvio da variação trimestral da taxa de câmbio nominal (R$/US$ ) em relação à sua variação de longo prazo prevista pela teoria da paridade do poder de compra
| date | cambio |
|---|---|
| 1999-01-01 | 51.3585532 |
| 1999-04-01 | -12.9274568 |
| 1999-07-01 | 1.5167101 |
| 1999-10-01 | -8.9134398 |
| 2000-01-01 | -9.4699371 |
| 2000-04-01 | -0.1940299 |
- Variável que captura choques de oferta provenientes de anomalias climáticas
- Dummy que assume valor 1 quando a anomalia climática é positiva (eventos El Niño)
- Dummy que assume valor 1 quando a anomalia climática é negativa (eventos La Niña)
| date | oni | d_elnino | d_lanina |
|---|---|---|---|
| 1999-01-01 | -1.306667 | 0 | 1 |
| 1999-04-01 | -1.013333 | 0 | 1 |
| 1999-07-01 | -1.123333 | 0 | 1 |
| 1999-10-01 | -1.456667 | 0 | 1 |
| 2000-01-01 | -1.380000 | 0 | 1 |
| 2000-04-01 | -0.720000 | 0 | 1 |
- Hiato do produto doméstico
| date | pib | pib_hp | hiato_produto |
|---|---|---|---|
| 1996-01-01 | 175440.8 | 179028.7 | -2.0040919 |
| 1996-04-01 | 177662.7 | 179901.8 | -1.2445930 |
| 1996-07-01 | 183826.3 | 180772.6 | 1.6892555 |
| 1996-10-01 | 182461.8 | 181637.6 | 0.4537454 |
| 1997-01-01 | 184299.6 | 182495.0 | 0.9888714 |
| 1997-04-01 | 185327.3 | 183343.5 | 1.0820316 |
- Expectativa da taxa Selic ao longo de um horizonte de doze meses
| date | selic_expec |
|---|---|
| 2005-01-01 | 16.50 |
| 2005-04-01 | 16.50 |
| 2005-07-01 | 16.00 |
| 2005-10-01 | 15.25 |
| 2006-01-01 | 14.00 |
| 2006-04-01 | 13.75 |
- Medida de hiato de taxa de juros real, obtida pela diferença entre a expectativa da taxa Selic ao longo de um horizonte de doze meses it,t+4|te e a expectativa de inflação referente ao mesmo período ( πt,t+4|te ), ambas apuradas pela pesquisa Focus e representadas em taxa anual, e uma taxa de juros real de equilíbrio não observável ( rr¯tIS )
| date | hiato_juros |
|---|---|
| 2023-10-01 | 5.1250 |
| 2024-01-01 | 5.5394 |
| 2024-04-01 | 6.3902 |
| 2024-07-01 | 7.5519 |
| 2024-10-01 | 9.7997 |
| 2025-01-01 | NA |
- Medida do resultado primário do governo central corrigido por outliers e ajustado pelo ciclo econômico, expressa como desvio de sua tendência
| date | rp | rp_hp | rp_hiato |
|---|---|---|---|
| 1991-10-01 | -0.9800000 | -1.551224 | 0.5712242 |
| 1992-01-01 | -0.8633333 | -1.562846 | 0.6995126 |
| 1992-04-01 | -1.3300000 | -1.574111 | 0.2441107 |
| 1992-07-01 | -1.5000000 | -1.584224 | 0.0842242 |
| 1992-10-01 | -1.2533333 | -1.592240 | 0.3389064 |
| 1993-01-01 | -1.7733333 | -1.597158 | -0.1761755 |
- Choque autorregressivo
| date | is_choque_ar |
|---|---|
| 1996-01-01 | 0.5532097 |
| 1996-04-01 | -0.0764221 |
| 1996-07-01 | 0.8098506 |
| 1996-10-01 | -1.9683965 |
| 1997-01-01 | 0.0073228 |
| 1997-04-01 | 1.6115114 |
- Meta para a taxa Selic nominal
| date | selic |
|---|---|
| 1999 Q1 | 42.0 |
| 1999 Q2 | 21.0 |
| 1999 Q3 | 19.0 |
| 1999 Q4 | 19.0 |
| 2000 Q1 | 18.5 |
| 2000 Q2 | 17.5 |
- Meta de inflação
| date | meta_inflacao |
|---|---|
| 1999-01-01 | 8 |
| 1999-04-01 | 8 |
| 1999-07-01 | 8 |
| 1999-10-01 | 8 |
| 2000-01-01 | 6 |
| 2000-04-01 | 6 |
- Taxa de juros de equilíbrio
| date | juros_equilibrio |
|---|---|
| 2005-01-01 | 10.870183 |
| 2005-04-01 | 10.553528 |
| 2005-07-01 | 10.236979 |
| 2005-10-01 | 9.921233 |
| 2006-01-01 | 9.607660 |
| 2006-04-01 | 9.298133 |
O código que gera estas tabelas individuais de variáveis é bastante simples e, portanto, pouco robusto e com espaço para melhorias.
Ao final de todo este processo, podemos cruzar as tabelas de dados de modo a obter uma única tabela de variáveis para o MPP:
| date | ipca_expec | ipca_livres | ipca_livres_sa | ipca | ipca_sa | ic_br | ic_br_agro | ic_br_energia | ic_br_metal | cambio | oni | d_elnino | d_lanina | pib | pib_hp | hiato_produto | selic_expec | hiato_juros | rp | rp_hp | rp_hiato | is_choque_ar | selic | meta_inflacao | juros_equilibrio |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2024-07-01 | 3.9481 | 1.4457583 | 0.9844238 | 1.42 | 1.049972 | -2.464639 | -1.06103 | -9.568977 | -1.387618 | 1.831694 | -0.0966667 | 0 | 0 | 336725.8 | 332307.0 | 1.3297416 | 11.50 | 7.5519 | 2.286667 | 1.0752876 | 1.2113791 | -0.2734256 | 10.75 | 3 | 7.350497 |
| 2024-10-01 | 4.9503 | 0.8622929 | 1.1529477 | 1.05 | 1.371823 | 13.011769 | 15.39948 | 9.649049 | 6.317956 | 9.022376 | -0.3866667 | 0 | 0 | 337306.9 | 334298.1 | 0.9000511 | 14.75 | 9.7997 | 1.366667 | 1.0279393 | 0.3387274 | -1.3678932 | 12.25 | 3 | 7.681013 |
| 2025-01-01 | 5.1852 | 0.3903861 | 0.8988515 | 0.80 | 1.209509 | NA | NA | NA | NA | NA | -0.6400000 | 0 | 1 | NA | NA | NA | NA | NA | 0.370000 | 0.9802096 | -0.6102096 | NA | 14.25 | 3 | NA |
| 2025-04-01 | NA | 2.1245766 | 1.7867778 | 1.48 | 1.117854 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 3 | NA |
| 2025-07-01 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 3 | NA |
| 2025-10-01 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 3 | NA |
Conclusão
Modelos de previsão macroeconômica podem facilmente alcançar um número elevado de variáveis. Mesmo modelos simplificados, como o Modelo de Pequeno Porte (MPP) do Banco Central, usam cerca de 30 variáveis. Isso impõe um grande desafio ao nosso dia a dia: como fazer a gestão destes dados para uso em modelos, desde a coleta até o tratamento?
Quer aprender mais?
Conheça nossa Formação Do Zero à Análise de Dados Econômicos e Financeiros usando a Linguagem R . Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros usando a Linguagem R.