Previsões com Vetores Autoregressivos no Python
Modelos Vetoriais AutoRegressivos (VAR) são amplamente utilizados na análise de séries temporais macroeconômicas. Eles permitem modelar a dinâmica conjunta de várias variáveis, capturando como choques em uma afetam as demais ao longo do tempo. Neste exercício, mostramos como aplicar um modelo VAR a um conjunto de dados macroeconômicos brasileiros para gerar previsões.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Vetores AutoRegressivos (VAR)
O modelo VAR(p) para um vetor de variáveis endógenas 
é dado por:
![\[\mathbf{y}_t = A_1 \mathbf{y}_{t-1} + A_2 \mathbf{y}_{t-2} + \dots + A_p \mathbf{y}_{t-p} + \varepsilon_t,\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-19534720d6c825b17b89049e1fe243e6_l3.png "Rendered by QuickLaTeX.com")
onde:
- é um vetor 
de variáveis endógenas,
- 
são matrizes de coeficientes 
,
- 
é um vetor de inovações com média zero e covariância constante.
Exemplo econômico com Vetores AutoRegressivos
Vamos aplicar o modelo VAR a um conjunto de séries macroeconômicas mensais:
- Inflação acumulada em 12 meses (IPCA);
- Expectativas de inflação para os próximos 12 meses (EIPCA);
- IC-Br (Indicador de Commodities do Banco Central);
- Câmbio BRL/USD;
- Taxa Selic (anualizada);
- Taxa de desemprego (PNAD Contínua);
- IBC-Br (proxy mensal do PIB).
Dados
As séries são mensais, com origem em fontes como IBGE e BCB. Abaixo, visualizamos as séries presentes na modelagem.
Passos para a Previsão de Vetores AutoRegressivos
1. Verificar estacionariedade das séries com o teste de Phillips-Perron (PP);
2. Diferenciar as séries quando necessário para garantir estacionariedade;
3. Dividir os dados em conjuntos de treino e teste;
4. Determinar a ordem ótima de defasagem do VAR;
5. Estimar o modelo VAR com as séries estacionárias;
6. Realizar previsões para o período de teste.
Obs. para aplicar VAR em variáveis não estacionárias em nível e estacionárias em I(1) é importante a verificação de cointegração, entretando, deixamos de lado esse procedimento.
Estacionariedade das variáveis
Realizamos o teste de Phillips-Perron (PP). O resultado está resumido abaixo:
| Variável | PP Nível (p-valor) | PP 1ª Dif. (p-valor) | Conclusão |
|---|---|---|---|
| IPCA | 0.1564 | 0.0000 | 1ª Dif. Estacionária |
| Desemprego | 0.6642 | 0.0000 | 1ª Dif. Estacionária |
| EIPCA | 0.4175 | 0.0000 | 1ª Dif. Estacionária |
| Câmbio | 0.7224 | 0.0000 | 1ª Dif. Estacionária |
| Selic | 0.4578 | 0.0001 | 1ª Dif. Estacionária |
| IC-Br | 0.7591 | 0.0000 | 1ª Dif. Estacionária |
| IBC-Br | 0.0000 | 0.0000 | Estacionária |
Como a maioria das séries são integradas de ordem 1 (I(1)), utilizamos as primeiras diferenças para garantir estacionariedade no VAR.
Separacão Treino-Teste
Dividimos a amostra em duas partes:
- Treino: Dados até 12 meses antes do fim da amostra.
- Teste: Os últimos 12 meses, usados para avaliar a capacidade preditiva.
Determinação da Ordem de Defasagem do VAR
A ordem ideal do modelo foi determinada com base nos critérios AIC, BIC, FPE e HQIC:
VAR Order Selection (* highlights the minimums)
==================================================
AIC BIC FPE HQIC
--------------------------------------------------
0 -3.241 -1.576 0.03921 -2.565
1 -10.70 -7.976* 2.279e-05 -9.593*
2 -10.88 -7.096 1.941e-05 -9.343
3 -11.10 -6.253 1.618e-05* -9.129
4 -11.03 -5.125 1.831e-05 -8.630
5 -11.15 -4.191 1.754e-05 -8.325
6 -11.30 -3.281 1.696e-05 -8.043
7 -11.28 -2.193 2.044e-05 -7.585
8 -11.36 -1.220 2.319e-05 -7.240
9 -11.79 -0.5877 2.002e-05 -7.238
10 -12.03* 0.2321 2.277e-05 -7.047
--------------------------------------------------Apesar do AIC sugerir ordem 10, usamos ordem 1 (com menor BIC e HQIC), para evitar sobreparametrização.
Previsão do Vetor Autoregressivo
Com o modelo estimado, realizamos previsões para os próximos 12 meses usando:
![\[\hat{\mathbf{y}}_{t+1} = A_1 \mathbf{y}_{t} + \hat{\varepsilon}_{t+1}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-a7a2087eaaf0c5e802750474f6a9876a_l3.png "Rendered by QuickLaTeX.com")
Assim comparamos as previsões dos dados de treinos com os valores observados contidos nos dados de teste.
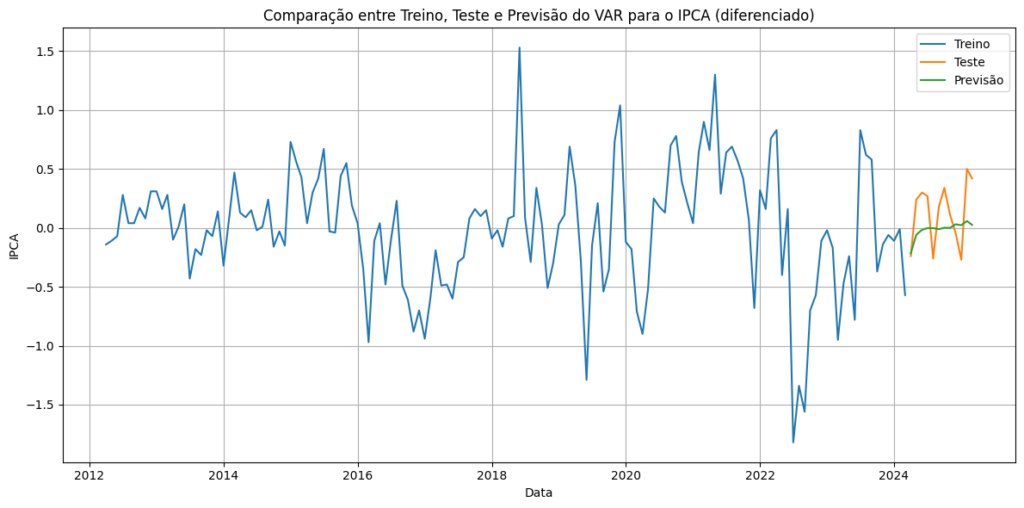
Por conta da característica de um modelo Vetorial AutoRegressivo, é possível prever todas as séries do sistema, mas no gráfico abaixo mostramos somente a previsão da série do IPCA em 12 meses diferenciado.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.
Referências:
- Lütkepohl, H. (2005). New Introduction to Multiple Time Series Analysis.
- Enders, W. (2014). Applied Econometric Time Series.
- Statsmodels documentation - VAR
