Como construir um Vetor Autoregressivo Estrutural (SVAR) no Python?
O modelo Vetor Autoregressivo Estrutural, conhecido como SVAR, tem como objetivo permitir a identificação e interpretação de choques estruturais — como um choque de política monetária ou de oferta — e seus impactos dinâmicos sobre variáveis macroeconômicas. A construção de um SVAR parte da estimação de um modelo VAR tradicional, seguido da imposição de restrições identificadoras com base em fundamentos econômicos.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
A forma reduzida de um modelo VAR(p) pode ser representada da seguinte maneira:
onde é um vetor com
variáveis endógenas,
são as matrizes de coeficientes e
representa o vetor de erros. A chave do SVAR está na suposição de que esses erros são combinações lineares de choques estruturais
, ou seja:
com sendo a matriz de impacto contemporâneo e
, implicando que os choques estruturais são ortogonais entre si. O objetivo da modelagem é justamente estimar essa matriz
, que captura como cada choque afeta diretamente as variáveis no mesmo período.
Objetivo do exercício:
- Preparar os dados macroeconômicos para análise, aplicando diferenciação para garantir estacionariedade.
- Estimar um modelo VAR com seleção automática da ordem de defasagem.
- Estruturar e identificar um modelo SVAR com base em restrições econômicas.
- Gerar e interpretar funções de impulso-resposta (IRFs) a choques estruturais.
- Analisar a matriz estrutural estimada para entender os impactos contemporâneos dos choques.
A seguir, implementamos esse processo em Python utilizando a biblioteca statsmodels.
1. Preparação dos dados
Neste exemplo, partimos de uma base contendo variáveis mensais da economia brasileira: PIB, IPCA e a taxa Selic. Os dados são trimestralizados e diferenciados para garantir estacionariedade antes da estimação do VAR.
| desem | ipca | juros | |
|---|---|---|---|
| Data | |||
| 2002-07-01 | -0.9 | 1.13 | 0.1325 |
| 2002-10-01 | -2.5 | 3.87 | 0.5691 |
| 2003-01-01 | 2.3 | -1.38 | 0.6495 |
| 2003-04-01 | 3.3 | -3.62 | 0.1150 |
| 2003-07-01 | 0.5 | -0.11 | -0.1557 |
2. Estimação do modelo VAR
Com os dados estacionários, o próximo passo é a estimação do modelo VAR, que será a base para a estruturação do SVAR. Utilizamos critérios de informação para escolher a ordem de defasagem adequada.
Através de uma função do próprio statsmodels, conseguimos obter a seguinte tabela abaixo:
VAR Order Selection (* highlights the minimums)
==================================================
AIC BIC FPE HQIC
--------------------------------------------------
0 -2.711 -2.584 0.06648 -2.665
1 -3.179 -2.673 0.04170 -2.996
2 -4.216 -3.329* 0.01493 -3.895
3 -4.562 -3.295 0.01079 -4.104
4 -4.567 -2.920 0.01118 -3.972
5 -4.464 -2.437 0.01327 -3.731
6 -4.342 -1.936 0.01669 -3.472
7 -4.748 -1.961 0.01307 -3.740
8 -5.043 -1.876 0.01235 -3.898
9 -5.495 -1.949 0.01120 -4.213
10 -6.357* -2.430 0.008146* -4.937*
--------------------------------------------------
Pelos resultados, vemos que para o critério AIC o número ótimo é de 10 defasagens, para o BIC 2 defasagens, FPE 10 defasgens e HQ 10 defasagens. Prosseguimos escolhendo 2 defasagens conforme BIC. Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Tue, 15, Apr, 2025
Time: 09:53:58
--------------------------------------------------------------------
No. of Equations: 3.00000 BIC: -2.61454
Nobs: 48.0000 HQIC: -3.12382
Log likelihood: -100.931 FPE: 0.0324872
AIC: -3.43319 Det(Omega_mle): 0.0215947
--------------------------------------------------------------------
Results for equation desem
===========================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------
const -0.454634 0.211205 -2.153 0.031
L1.desem 0.075242 0.124081 0.606 0.544
L1.ipca 0.413278 0.237908 1.737 0.082
L1.juros -2.734034 0.720204 -3.796 0.000
L2.desem -0.306499 0.126321 -2.426 0.015
L2.ipca 0.549238 0.223798 2.454 0.014
L2.juros 3.399131 0.729298 4.661 0.000
===========================================================================
Results for equation ipca
===========================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------
const -0.262259 0.091059 -2.880 0.004
L1.desem -0.185704 0.053497 -3.471 0.001
L1.ipca -0.279042 0.102572 -2.720 0.007
L1.juros -0.086323 0.310510 -0.278 0.781
L2.desem -0.115456 0.054462 -2.120 0.034
L2.ipca -0.552082 0.096489 -5.722 0.000
L2.juros -0.617637 0.314431 -1.964 0.049
===========================================================================
Results for equation juros
===========================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------
const -0.037054 0.035888 -1.032 0.302
L1.desem -0.028235 0.021084 -1.339 0.181
L1.ipca 0.034067 0.040426 0.843 0.399
L1.juros 0.544050 0.122378 4.446 0.000
L2.desem 0.017286 0.021465 0.805 0.421
L2.ipca 0.150890 0.038028 3.968 0.000
L2.juros -0.195683 0.123923 -1.579 0.114
===========================================================================
Correlation matrix of residuals
desem ipca juros
desem 1.000000 -0.422901 -0.016842
ipca -0.422901 1.000000 0.163622
juros -0.016842 0.163622 1.000000
3. Construção do modelo SVAR
Para identificar o modelo, impomos restrições sobre a matriz A. Quando não impomos restrições sobre a matriz B, assumimos que a matriz de covariância dos erros estruturais é a identidade I, ou seja, não há restrições estruturais sobre os choques, apenas sobre os efeitos contemporâneos entre as variáveis.
| desem | ipca | juros | |
|---|---|---|---|
| desem | 1.496835 | -0.272918 | -0.004284 |
| ipca | -0.272918 | 0.278236 | 0.017943 |
| juros | -0.004284 | 0.017943 | 0.043219 |
A matriz de covariância mostra que os valores fora da diagonal são diferentes de zero, implicando que A≠I. Dessa forma, a especificação reduzida pode não ser a mais correta. Assim, de modo a incluir efeitos contemporâneos, devemos impor uma diferente estrutura para a matriz A. Para isso, vamos supor que o desemprego é afetado somente pela taxas de juros contemporaneamente, e que a inflação é afetada pelo desemprego contemporaneamente.
Finalmente, assumimos que a taxa de juros é determinada somente por defasagens das outras variáveis. Esta última hipótese também pode ser interpretada como o Banco Central não sendo capaz de observar o nível de desemprego e preços no mesmo instante que irá determinar a taxa de juros. Assim, nossa matriz A deveria ser algo como
Abaixo estimamos o modelo estrutural e obtemos os IRFs impondo a restrição acima.
VAR Order Selection (* highlights the minimums)
==================================================
AIC BIC FPE HQIC
--------------------------------------------------
0 -2.711 -2.584 0.06648 -2.665
1 -3.179 -2.673 0.04170 -2.996
2 -4.216 -3.329* 0.01493 -3.895
3 -4.562 -3.295 0.01079 -4.104
4 -4.567 -2.920 0.01118 -3.972
5 -4.464 -2.437 0.01327 -3.731
6 -4.342 -1.936 0.01669 -3.472
7 -4.748 -1.961 0.01307 -3.740
8 -5.043 -1.876 0.01235 -3.898
9 -5.495 -1.949 0.01120 -4.213
10 -6.357* -2.430 0.008146* -4.937*
--------------------------------------------------4. Respostas a impulso (IRFs) no SVAR
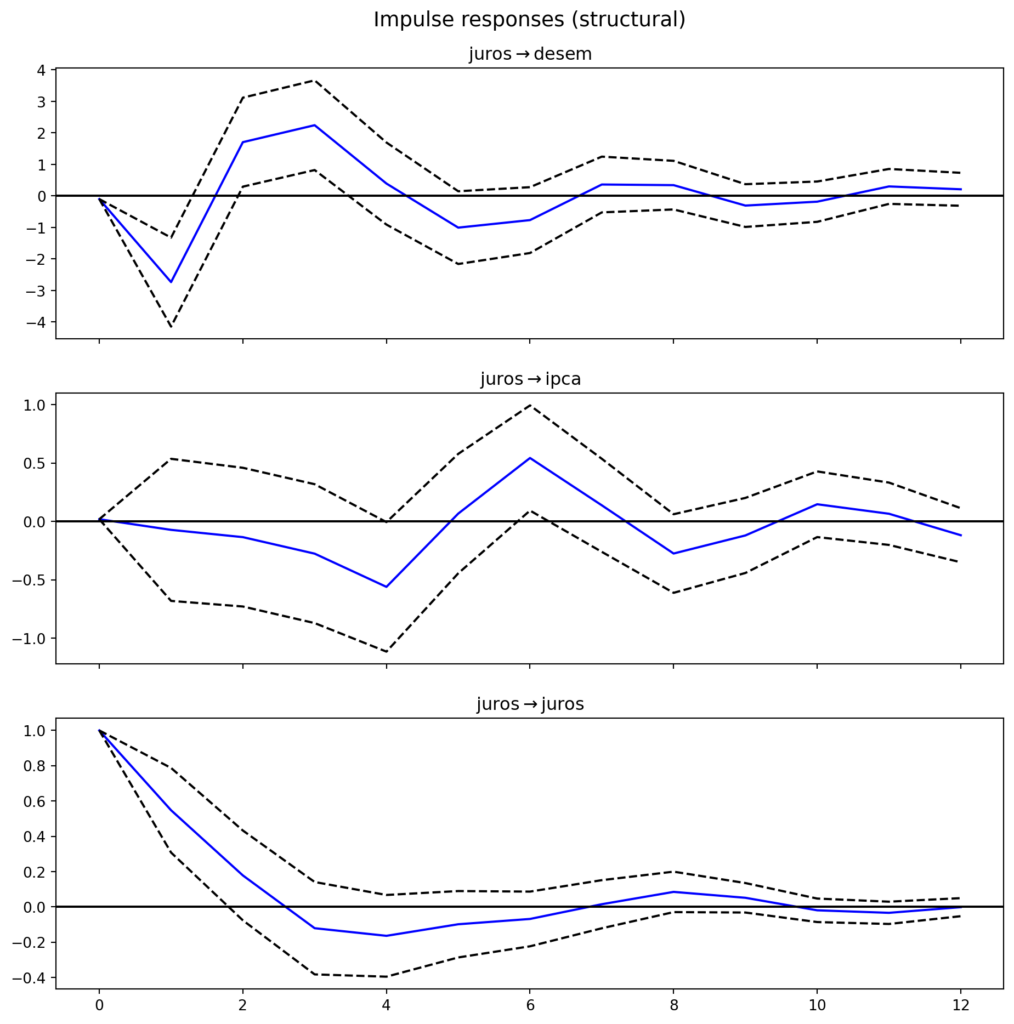
A Função de Resposta ao Impulso (IRF) apresentada estima o impacto de um choque na taxa de juros sobre o desemprego, a inflação (IPCA) e a própria taxa de juros ao longo do tempo. Importante relembrar que os dados estão em primeira diferença.
É importante ressaltar que esse exercício foi construído com o objetivo didático de mostrar como estruturar e estimar um modelo SVAR no Python. O modelo utilizado conta com apenas três variáveis e uma defasagem, o que limita sua capacidade de capturar as interações reais e complexas da economia.
5. Interpretação da matriz estrutural do SVAR
A matriz , estimada a partir do modelo, expressa como os choques estruturais impactam contemporaneamente as variáveis do sistema. Sua interpretação depende da ordem assumida das variáveis no vetor
.
Matriz B estimada:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]O exercício acima permite construir um modelo SVAR simples, mas completo, no Python. A escolha da ordem das variáveis, bem como o tipo de identificação adotada, deve sempre seguir uma lógica econômica clara e bem fundamentada. Isso garante que as inferências feitas a partir do modelo tenham validade causal.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.
Referências:
- Lütkepohl, H. (2005). New Introduction to Multiple Time Series Analysis.
- Enders, W. (2014). Applied Econometric Time Series.
- Statsmodels documentation - VAR

![Rendered by QuickLaTeX.com \[A = \begin{bmatrix} 1 & 0 & \alpha\\ \alpha & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}. \nonumber\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-98dfb78367a92815a9b31e4e91f5b7f9_l3.png)
