Nos últimos meses, o dono deste blog, Vitor Wilher, vem sendo repetitivo em relação aos supostos equívocos que alguns economistas têm cometido, mais especificamente o fato de acreditarem que inflação possa trazer benefícios (leia-se crescimento econômico) de longo prazo para a economia brasileira. O objetivo deste post é justamente tentar provar que o Vitor está errado, isto é, mostrar que existe sim uma relação positiva de longo prazo entre inflação e PIB (uma breve explicação sobre relações de longo prazo e cointegração pode ser encontrada aqui).
É possível gerar crescimento econômico através da geração de inflação ?
Farei isto utilizando métodos simples, dado que só envolvem regressões simples usando MQO e testes de raíz unitária, porém comumente utilizados na literatura, portanto, os leitores com pouca experiência em econometria poderão aprender como testar relações de longo prazo / teorias econômicas de maneira simples. Veja outro exemplo do uso de testes de cointegração aqui.
A minha intenção aqui será ser o mais transparente e sincero o possível, logo, caso alguém queira "testar" os meus resultados é só pedir que disponibilizo os dados e os códigos aqui utilizados.
Para tentar cumprir com o meu objetivo irei usar o log das séries do IPCA e do PIB*, que podem ser vistas abaixo.
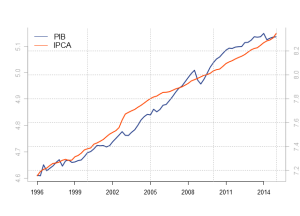
Bom, primeiramente, dado que o foco aqui é estimar uma relação de longo prazo, estamos na verdade interessados em estimar um modelo de correção de erros, ou Error Correction Model (ECM) no inglês. Porém, para isso é preciso primeiro determinar se as séries em questão são integradas da mesma ordem (e numa ordem maior que 0). Para isto usei o teste ADF sequencial**.
A tabela a seguir*** mostra o último passo do teste ADF sequencial e, a partir desta, eu concluo que as duas séries em questão são ambas I(1). Isto é, são integradas de primeira ordem, ou simplesmente que a primeira diferença das séries é estacionária.
| 1% | 5% | 10% | |||
| -5.45 | -3.71 | -4.04 | -3.45 | -3.15 | |
| 9.95 | 4.67 | 6.50 | 4.88 | 4.16 | |
| 14.92 | 6.91 | 8.73 | 6.49 | 5.47 |
Como estamos utilizando o logaritmo das séries, podemos considerar a primeira diferença destas como uma boa aproximação para sua variação percentual trimestral. Os dados estacionários estão apresentados a seguir.
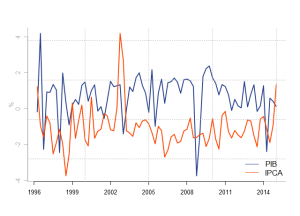
Agora que estabelecemos a ordem de integração, podemos continuar com a estimação da possível relação de longo prazo. Para isso, irei seguir o método de Engle-Granger em dois passos que consiste em:
i) Estimar um MQO com as variáveis não estacionárias;
e, se resíduos do MQO forem estacionários,
ii) Estimar um ECM.
Portanto, primeiro irei estimar um MQO com as séries não estacionárias, para então ver se a combinação linear entre as séries, ou seja, os resíduos, são estacionários. O resultado está resumido abaixo.
| Estimativa | t | |
| Intercepto | 1.00 | 3.55 |
| IPCA | 0.50 | 12.89 |
Apesar dos testes de significância não seguirem distribuições normais, podemos ver que o coeficiente da regressão é positivo e que aparentemente é bastante significativo. Logo, se isto não se tratar de uma regressão espúria, isto poderia ser um indicativo de que existe sim uma relação positiva de longo prazo entre PIB e o IPCA (isto é, contrariando o que é dito pelo dono deste blog).
Em seguida, aplico um teste ADF aos resíduos****. O valor crítico do teste se situa em torno de -3.40 enquanto que a estatística de teste estimada está em -1.86. Logo, rejeito a hipótese de que os resíduos da regressão são estacionários e, consequentemente, a regressão é espúria.
Portanto, não há cointegração entre PIB e IPCA. Neste instante os críticos ou céticos poderiam dizer: "Ah, mas você não tentou isso/aquilo...!". Pois é leitores, como eu normalmente sou um desses céticos eu me preparei e aqui vai um breve resumo do que eu fiz, além desse exercício acima, na minha busca em provar que o dono deste blog estava errado em criticar certos economistas:
i) Estimei a relação inversa, ou seja, assumindo o IPCA como endógeno (apesar do fato de que, em havendo cointegração, os resultados deveriam ser assintoticamente iguais);
ii) Usei variações anuais ao invés de trimestre contra trimestre;
iii) Testei a hipótese (mais forte ainda ?) de que a relação seria entre IPCA e PIB Potencial. Para isto estimei 3 diferentes versões de PIB Potencial, todos baseados no filtro HP porém com parâmetros variando de 25 até aproximadamente 100000 de forma a simular diferentes períodos de "ajuste" do PIB potencial.
Infelizmente, para os economistas aos quais o Vitor se refere, neste exercício não consegui achar nenhuma relação de longo prazo. Obviamente, poderia-se repetir este exercício utilizando mais de uma série como um "teste de robustez", porém deixo isto para o leitor mais interessado (leia sobre o Teste de Johansen).
Finalizando, gostaria de deixar bem claro que se alguém conseguir encontrar essa relação, por favor não hesite em entrar em contato comigo ou com o Vitor Wilher!
* A série do PIB é trimestral e dessazonalizada enquanto o índice do IPCA é mensal, logo tornei a série do IPCA trimestral tomando as médias de cada trimestre.
** Como demonstrado em Enders (2009) e Pfaff (2008).
*** Aqui utilizo a mesma notação que Pfaff (2008).
**** Porém não utilizo os valores críticos sugeridos pela tabela Dickey-Fuller comum e sim pelos valores EG-ADF sugeridos em Enders (2009).

