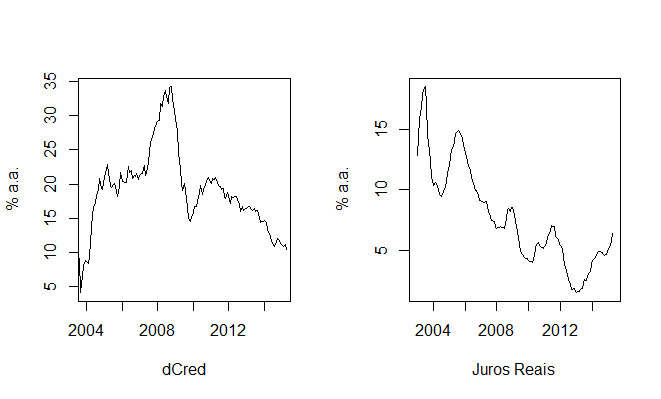Tenho sido repetitivo em minhas apresentações sobre o impacto dos empréstimos do BNDES na economia brasileira. De forma geral, mostro que a despeito dos quase R$ 500 bilhões que o Tesouro colocou no banco nos últimos anos, a taxa de investimento da economia brasileira não aumentou; ao contrário, diminuiu entre 2008 e 2014. Entender as razões pelas quais o investimento pouco reagiu ao aumento do crédito público passa pela compreensão do processo de crescimento econômico. Você pode saber sobre isso lendo o livro do professor Acemoglu. Mas o aumento do crédito público vis a vis o crédito privado gera um pouco mais de distorções sobre a economia. A concessão desse tipo de crédito não envolve, necessariamente, uma decisão técnica, mas por vezes questões políticas. Além disso, a ele estão associadas taxas de juros subsidiadas, que não respondem a mudanças na taxa básica de juros. Com efeito, o aumento da sua participação no crédito total acaba por "entupir" o canal de crédito, fazendo com que o Banco Central tenha que aumentar mais os juros para atingir a inflação. Nesse post vamos fazer um breve exercício que relaciona a expansão do crédito público à perda de eficiência da política monetária brasileira.
Para fazer isso, achei que seria interessante, em primeiro lugar, decompor a parte do crédito que reage a taxa de juros e outra que não reage. Para tal, tomei emprestada a equação de Bolle (2010), da forma que segue:
(1)
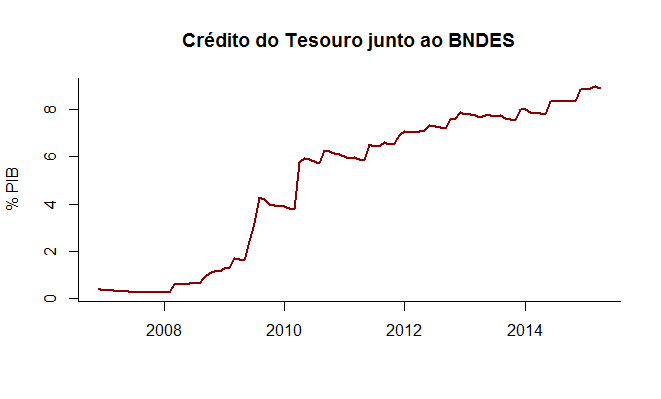
A equação acima relaciona a variação em 12 meses do crédito total da economia a uma constante e aos juros reais, dados pela diferença entre a taxa básica de juros (Selic) e as expectativas de inflação 12 meses à frente. Desse modo, temos o crédito decomposto em duas partes: uma que é sensível aos juros reais e outro que não é (a constante). Os gráficos do crédito e dos juros reais são postos abaixo.
Antes de rodar a regressão, temos que ver se as séries são estacionárias. Pelos gráficos acima, parece que não são. Para confirmar, fiz uso do teste ADF Sequencial, conforme Pfaff (2008). As tabelas para a equação de teste com drift e tendência, com tendência e sem nenhum dos dois são postas abaixo.
| dCred | Juros Reais | 1pct | 5pct | 10pct | |
| tau3 | -1.927 | -2.716 | -3.990 | -3.430 | -3.130 |
| phi2 | 3.098 | 2.519 | 6.220 | 4.750 | 4.070 |
| phi3 | 4.641 | 3.778 | 8.430 | 6.490 | 5.470 |
| dCred | Juros Reais | 1pct | 5pct | 10pct | |
| tau2 | -1.156 | -1.428 | -3.460 | -2.880 | -2.570 |
| phi1 | 0.674 | 1.020 | 6.520 | 4.630 | 3.810 |
| dCred | Juros Reais | 1pct | 5pct | 10pct | |
| tau1 | -0.359 | -0.662 | -2.580 | -1.950 | -1.620 |
Observa-se que nas três equações do teste ADF não podemos rejeitar a hipótese nula de existência de raiz unitária. Faz-se, desse modo, o mesmo teste para a primeira diferença das séries, chegando à conclusão que ambas são integradas de ordem 1. Com efeito, podemos prosseguir com o exercício, tendo em mente a possibilidade de cointegração entre as séries.
Regressão para todo o intervalo da amostra
Em uma primeira regressão, pegamos todo o período da amostra, que vai de janeiro de 2003 a abril de 2015. Os resultados são postos abaixo.
| Dependent variable: | |
| dCred | |
| Juros Reais | -0.060 |
| (0.123) | |
| Constante | 19.174*** |
| (1.070) | |
| Observations | 148 |
| R2 | 0.002 |
| Adjusted R2 | -0.005 |
| Residual Std. Error | 6.081 (df = 146) |
| F Statistic | 0.239 (df = 1; 146) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
O resultado é frustrante, não é mesmo? Ao rodar a regressão para todo o período, nada se pode inferir sobre o comportamento da variação do crédito. Diante disso, e tendo em vista o avanço do crédito público, uma opção que pensei foi rodar a regressão até 2008, apenas para entender se os resultados frustrantes se manteriam ou, de outra forma, conseguiria um quadro melhor.
O mercado de crédito antes da "marolinha"...
A saída da regressão é posta abaixo:
| Dependent variable: | |
| dCred | |
| Juros Reais | -1.600*** |
| (0.201) | |
| Constante | 37.779*** |
| (2.319) | |
| Observations | 69 |
| R2 | 0.487 |
| Adjusted R2 | 0.479 |
| Residual Std. Error | 5.175 (df = 67) |
| F Statistic | 63.622*** (df = 1; 67) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
Bem melhor, não? Antes de qualquer coisa, fazemos o teste ADF Sequencial, conforme Pfaff (2008), sobre os resíduos, conforme a tabela abaixo. Podemos rejeitar a hipótese nula, dada a comparação da estatística tau3 com os valores críticos. Isto é, os resíduos são estacionários e como as séries são integradas de ordem 1, temos evidências de que a variação do crédito e os juros reais são cointegrados, de modo que a regressão não é espúria. Você pode ver mais sobre isso em Enders (2009).
| Resíduos | 1pct | 5pct | 10pct | |
| tau3 | -4.202 | -4.040 | -3.450 | -3.150 |
| phi2 | 7.115 | 6.500 | 4.880 | 4.160 |
| phi3 | 9.085 | 8.730 | 6.490 | 5.470 |
Nesses termos, observa-se que para o período entre janeiro de 2003 a setembro de 2008, a variação do crédito em 12 meses pode ser explicada pela constante - a parte insensível aos juros - e pelos juros reais. Ademais, o coeficiente dos juros reais é negativo, indicando que um aumento deste causa menor crescimento no crédito total. A parte insensível aos juros pode ser, desse modo, interpretada como a parte do crédito público, enquanto a parte que responde a juros reais é representada pelo crédito privado.
Ora, o que aconteceu com a relação entre variação do crédito total e juros reais?
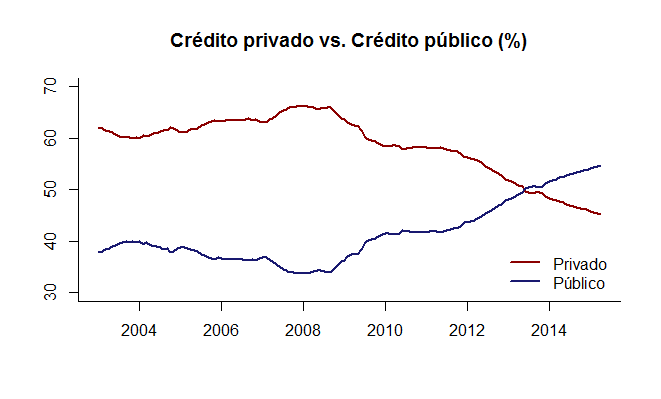
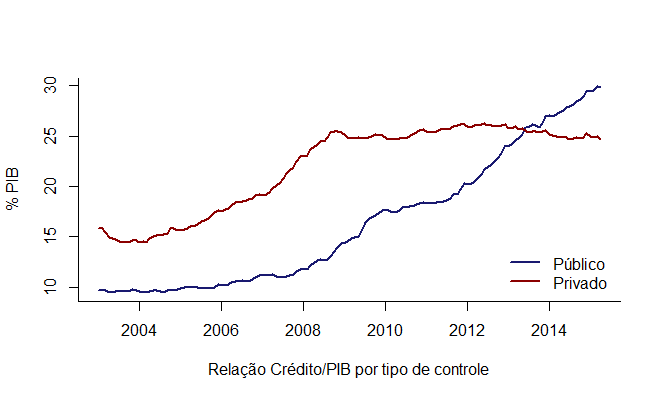
De 2008 para cá, como podemos inferir a partir do primeiro gráfico, o BNDES foi bastante capitalizado pelo Tesouro. Além disso, o governo passou a incentivar tanto o Banco do Brasil quanto a Caixa Econômica Federal a aumentarem os empréstimos à pessoa física. Isso gerou mudança no mercado de crédito? Para ver isso, colocamos os dois gráficos a seguir, que mostram o crédito total dividido por tipo de controle e essa divisão em relação ao PIB.
O crédito público não apenas avançou de 2008 para cá, como acabou tomando a dianteira do crédito privado. Em outros termos, como o crédito hoje tem grande participação de instituições estatais, é possível entender melhor os resultados daquela regressão para o período todo da nossa amostra. Isto porque, o crédito público é insensível aos juros reais.
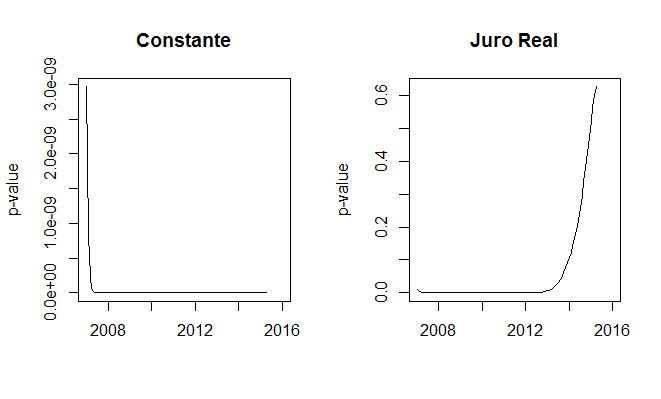
Para tornar a nossa compreensão sobre a relação entre variação do crédito total e juros reais melhor, uma última etapa do exercício compreende fazer a estimação recursiva, de modo a captar a evolução da relação. Começamos com uma amostra contendo 48 observações e vamos acrescentando cada nova observação à estimação. Com efeito, temos a evolução tanto da constante quanto dos juros reais. Mostramos abaixo o p-valor dos mesmos, de modo que o leitor passa a ter uma noção sobre quando os juros reais passaram a não se mais estatisticamente significativos.
A evolução do p-valor mostra que a partir de janeiro de 2014 o coeficiente dos juros reais passa a não ser mais estatisticamente significativo para explicar a variação do crédito total em 12 meses. Em outras palavras, esse exercício simples gera uma reflexão. Será que o aumento da participação do crédito público no crédito total reduziu a eficiência da política monetária? Ou, em outras palavras, será que o canal de crédito passou a responder menos a mudanças na taxa básica de juros? São questões importantes que estão colocadas e devem ser avaliadas com bastante cuidado.
A simplicidade do que fiz aqui não pode, claro, ser encarada como evidência definitiva, mas pode motivar estudos mais elaborados sobre o assunto. Dada a relevância do tema, acho importante que mais e mais economistas se envolvam na questão. E, para terminar, uma provocação: o seu economista favorito, que defendeu a expansão do BNDES nos últimos anos, o que pensa sobre o aumento de juros atual para controlar a inflação? Afinal, os juros saíram de 7,25% para 13,75% a.a. em termos nominais e a inflação de preços livres continua próxima a 7% a.a. Será que o crédito público que o seu economista favorito tanto defendeu tem algo a ver com isso? Não sei, deixo a resposta para você pensar... 🙂
_______________________________________________________
Bolle, M. B. (2010). O Retorno do Crédito Público. Carta Econômica Galanto nº 310.
Enders, W. (2009). Applied econometric time series. 3ª edição, Nova York: Wiley.
Pfaff, B. (2008). Analysis of Integrated and Cointegrated Time Series with R. Nova York: Springer.