O tema de hoje é uma tentativa de dialogar com um post recente do Leruaite Econômico, elaborado pelo Marcelino Guerra, sobre a relação entre política fiscal e inflação. Marcelino colocou uma função de reação fiscal no post, fez testes de quebra estrutural e chegou à observação de que no período posterior ao terceiro trimestre de 2011 o sinal do coeficiente da inflação teria se modificado. Ele teria passado a ser positivo, indicando um retrocesso em termos de política econômica. Como o Marcelino gentilmente me passou os dados que utilizou, eu aproveitei para fazer um exercício rápido no de modo a buscar um diálogo sobre esse que eu acho um campo bem interessante de estudo em macroeconomia aplicada. Ao trabalho, então?
Antes de mais nada, eu sou inclinado a concordar com as conclusões gerais do post do Marcelino. Acho mesmo que tanto a política fiscal quanto a monetária deixaram há muito tempo de se preocupar com a inflação. O problema para quem lida com dados, entretanto, é que isso não basta, não é mesmo? É preciso olhar os dados e tentar encontrar alguma forma de ver se, de fato, os mesmos mostram isso. É nessa direção que caminha o trabalho do Marcelino - não apenas nesse post, mas também ao longo da sua carreira acadêmica, como o leitor pode notar. Pensando nisso, vamos aos dados que ele me repassou?
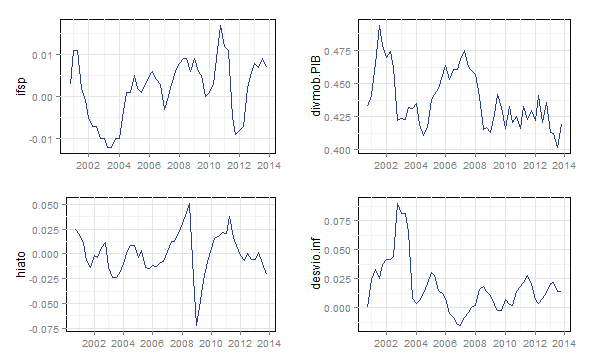
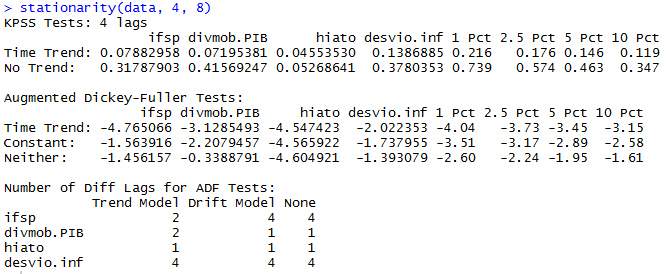
Os gráficos mostram séries trimestrais do impulso fiscal, dívida mobiliária em relação ao PIB, hiato do produto e desvio da inflação em relação à meta. Bom, leitor, para seguir o exercício, é preciso fazer um teste de raiz unitária. O teste ADF e o KPSS são mostrados a seguir.
Todas as séries passam no teste KPSS, enquanto no ADF, a relação dívida mobiliária em relação ao PIB e o desvio da inflação em relação à meta não conseguem rejeitar a hipótese nula. Marcelino fez em seu trabalho o DF-GLS e observou que todas as séries passaram no teste. Bom, dito isto, para prosseguir, vamos considerar que todas as séries são estacionárias em nível, mas pelo gráfico e pelo teste ADF, lembre-se que há ressalvas quanto a isso.
Nesse contexto, prossegui estimando a mesma função de reação fiscal que o Marcelino estimou:
(1)
Os resultados são postos na tabela abaixo.
| Dependent variable: | |
| Impulso Fiscal (IF) | |
| IF(-1) | 0.730*** |
| (0.085) | |
| Dívida(-1) | -0.037 |
| (0.026) | |
| Hiato(-1) | 0.029 |
| (0.028) | |
| Desvio | -0.068** |
| (0.026) | |
| Constant | 0.018 |
| (0.011) | |
| Observations | 52 |
| R2 | 0.730 |
| Adjusted R2 | 0.707 |
| Residual Std. Error | 0.004 (df = 47) |
| F Statistic | 31.823*** (df = 4; 47) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
Os coeficientes da Dívida e do hiato não são estatisticamente significativos, enquanto os coeficientes do desvio da inflação em relação à meta e do componente defasado do impulso fiscal são. O leitor pode comparar com os resultados encontrados pelo Marcelino. Há diferenças. Em particular, repare no coeficiente do desvio da inflação em relação à meta [que eu chamei, por ausência de criatividade, de Desvio]: ele é estatisticamente significativo e negativo, indicando que aumentos no mesmo fazem o governo reduzir o impulso fiscal.
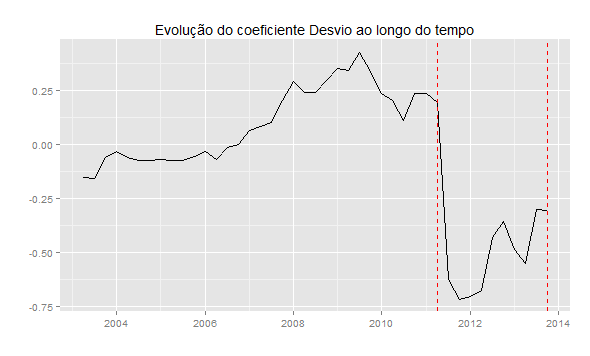
Como esse parece ser o ponto que Marcelino chamou mais atenção, eu procurei exercitá-lo melhor. Rodei uma rolling regression com diferentes períodos. O resultado final não parece ser sensível. Abaixo coloco um gráfico que mostra a evolução do coeficiente do Desvio para uma janela de 10 trimestres. Além disso, aplico a função cpt.meanvar do pacote changepoint. As linhas vermelhas tracejadas indicam o período em que houve mudança na média e na variância.
A primeira coisa que fica evidente é que há muito pouca estabilidade no coeficiente. Isso pode ser devido a problemas na estimação ou mesmo refletir uma opção de política econômica. A segunda coisa é que 2011 parece ser um ano de mudança no coeficiente. Em particular, o período em que o coeficiente fica positivo, nesse exercício, é entre o primeiro trimestre de 2007 e o segundo trimestre de 2011. Em outros termos, aumentos no desvio fariam o impulso fiscal ficar maior [e não menor, como seria o "normal"]. Ele volta a ficar negativo no terceiro trimestre de 2011 e se mantém assim até o final da amostra [quarto trimestre de 2013], apesar de ir se tornando "menos negativo".
O que aconteceu em 2011, leitor? Houve, de fato, um ajuste fiscal no primeiro ano do governo Dilma e isso pode explicar a mudança de positivo para negativo no coeficiente. Antes disso, entre 2007 e 2011, o governo manteve diversos programas de expansão do gasto público, como o programa de aceleração do crescimento. O fato do coeficiente ter se tornado positivo nesse período pode estar refletindo o tal "viés inflacionista" da política fiscal.
Um ponto importante é que o Marcelino e eu chegamos ao mesmo período de quebra: 2011. Os resultados é que não bateram: para a subamostra em que ele roda novamente a mesma equação, o coeficiente passa a ser positivo, enquanto na minha rolling regression o coeficiente se mantém negativo.
Acho que esse é um ponto de debate e diálogo, mas como em minha memória está o tal ajuste da Dilma em 2011, me parece que o resultado da rolling regression encontra-se mais aderente. Enfim, fica a minha contribuição e meu alerta enquanto macroeconomista aplicado: os dados nem sempre dizem o que você quer ouvir! Se o Marcelino ou outrem quiserem continuar a conversa, ficarei feliz em voltar ao tema! 🙂