Introdução
Neste exercício, avaliamos o impacto do aumento do programa Bolsa Família sobre as despesas orçamentárias totais das famílias brasileiras, utilizando dados da Pesquisa de Orçamentos Familiares (POF) 2017-2018. O método empregado foi o Propensity Score Matching (PSM), que visa emparelhar famílias que receberam o benefício com aquelas que não receberam, buscando controlar por possíveis vieses de seleção observáveis. A análise foi realizada em R, onde utilizamos diversos pacotes para coleta de dados, cálculo do propensity score, matching e estimativa dos efeitos.
Avaliação de Impacto e Propensity Score Matching
O Propensity Score Matching (PSM) é uma técnica de avaliação de impacto que permite simular as condições de um experimento controlado, emparelhando unidades de tratamento (famílias que recebem o Bolsa Família) com unidades de controle (famílias que não recebem o benefício), de forma que ambos os grupos sejam comparáveis em termos de características observáveis. O objetivo é estimar o Efeito Médio do Tratamento sobre os Tratados (ATT), ou seja, o impacto médio do aumento do Bolsa Família nas despesas orçamentárias totais das famílias beneficiadas.
Dados
Para realizar a análise, os dados foram coletados a partir da Base dos Dados, utilizando as tabelas referentes às despesas coletivas e informações dos moradores da POF 2017-2018. Tomamos como ponto de referência para o recebimento do Bolsa Família famílias com renda total per capita abaixo de 170 reais.
Modelo
Avaliação do Propensity Score
Após a coleta dos dados, foi implementado o cálculo do Propensity Score usando um modelo de regressão logística (glm) para prever a probabilidade de uma família ser beneficiada com o Bolsa Família, com base nas covariáveis como idade, sexo, raça/cor, anos de estudo, e região.
Código
Call:
glm(formula = tratamento ~ idade + sexo + raca_cor + anos_estudo +
situacao + regiao, family = binomial(), data = dados)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.017610 0.111253 0.158 0.874
idade -0.061917 0.001372 -45.133 < 2e-16 ***
sexo2 0.478163 0.034689 13.784 < 2e-16 ***
raca_cor2 0.292215 0.058692 4.979 6.40e-07 ***
raca_cor3 0.370513 0.246465 1.503 0.133
raca_cor4 0.252897 0.043282 5.843 5.13e-09 ***
raca_cor5 0.233691 0.211891 1.103 0.270
raca_cor9 -0.191785 0.426159 -0.450 0.653
anos_estudo -0.160653 0.004415 -36.385 < 2e-16 ***
situacao2 0.547094 0.037572 14.561 < 2e-16 ***
regiaonordeste 1.270255 0.072379 17.550 < 2e-16 ***
regiaonorte 1.377499 0.075863 18.158 < 2e-16 ***
regiaosudeste 0.518487 0.080322 6.455 1.08e-10 ***
regiaosul -0.032775 0.099705 -0.329 0.742
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 30596 on 57917 degrees of freedom
Residual deviance: 25480 on 57904 degrees of freedom
AIC: 25508
Number of Fisher Scoring iterations: 6- Idade (
idade, Coeficiente: -0.0619): A idade tem um impacto negativo significativo na probabilidade de uma família receber o Bolsa Família. Isso significa que, conforme a idade do chefe de família aumenta, a chance de receber o benefício diminui. - Sexo (
sexo2, Coeficiente: 0.4782): Mulheres têm uma probabilidade significativamente maior de receber o benefício, em comparação aos homens (sexo 1 é a classe de referência). - Raça/Cor:
raca_cor2(Coeficiente: 0.2922): Indivíduos da raça/cor 2 (pretos) têm maior chance de receber o Bolsa Família em relação à classe de referênciaraca_cor1(brancos).raca_cor4(Coeficiente: 0.2529): Pardos também têm uma maior chance em comparação à classe de referência.
- Anos de Estudo (
anos_estudo, Coeficiente: -0.1607): Quanto maior o nível de escolaridade, menor a probabilidade de a família ser beneficiada pelo Bolsa Família. Isso reflete a tendência de que o programa atenda famílias com menor escolaridade. - Região:
- Nordeste (
regiaonordeste, Coeficiente: 1.2703): Famílias da região Nordeste têm uma probabilidade muito maior de serem beneficiadas em relação àquelas do Centro-Oeste (classe de referência). - Norte (
regiaonorte, Coeficiente: 1.3775): Famílias da região Norte também têm maior probabilidade de serem beneficiadas.
- Nordeste (
Avaliação do Pareamento
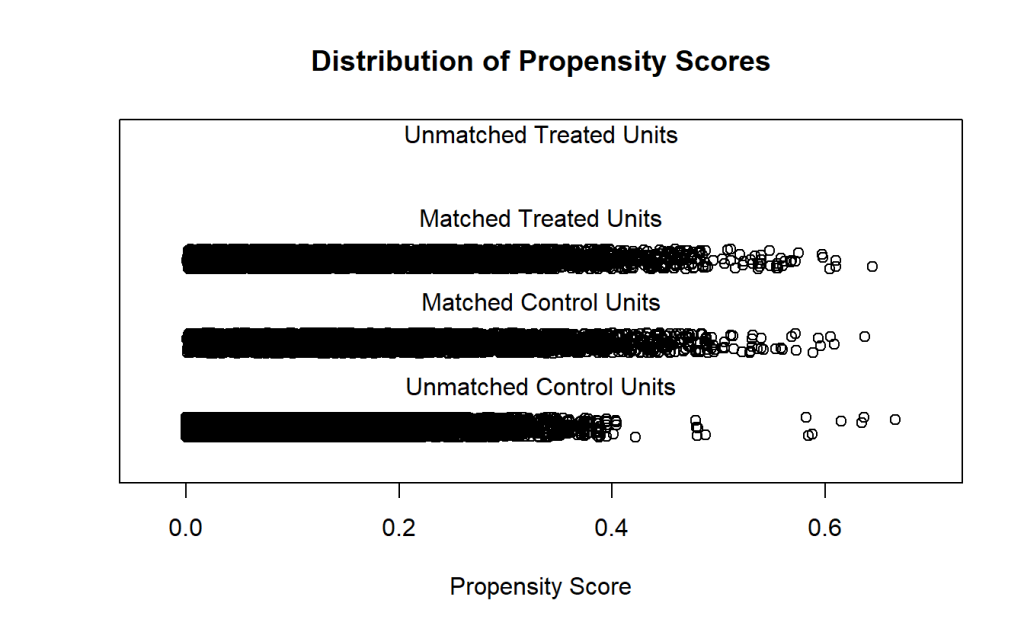
Utilizamos o método de Nearest Neighbor Matching para emparelhar as famílias tratadas com as não tratadas, com base no propensity score calculado.
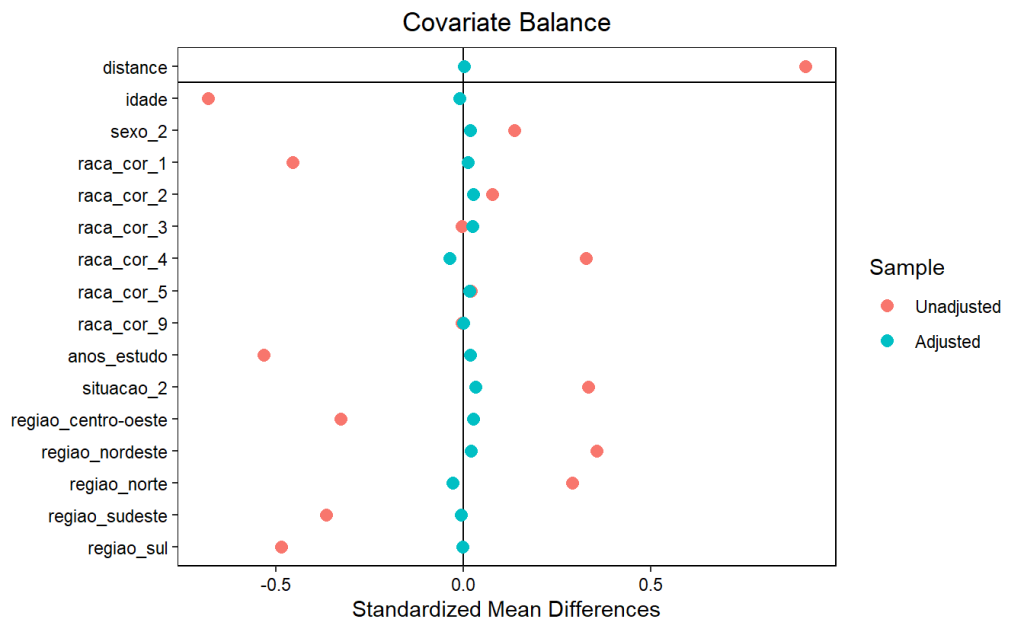
Após o pareamento, o balanceamento das covariáveis foi avaliado, mostrando que o processo de matching reduziu consideravelmente os desvios entre os grupos de tratamento e controle, tornando os grupos comparáveis.
Código
Call: matchit(formula = tratamento ~ idade + sexo + raca_cor + anos_estudo + situacao + regiao, data = dados, method = "nearest", distance = "glm", link = "probit") Summary of Balance for All Data: Means Treated Means Control Std. Mean Diff. Var. Ratio distance 0.1742 0.0661 0.9124 2.5488 idade 41.7223 50.5102 -0.6815 0.6665 sexo1 0.5217 0.5895 -0.1358 . sexo2 0.4783 0.4105 0.1358 . raca_cor1 0.2088 0.3938 -0.4552 . raca_cor2 0.1393 0.1125 0.0774 . raca_cor3 0.0049 0.0053 -0.0052 . raca_cor4 0.6384 0.4814 0.3268 . raca_cor5 0.0070 0.0052 0.0210 . raca_cor9 0.0016 0.0018 -0.0044 . anos_estudo 6.1500 8.3544 -0.5322 0.6995 situacao1 0.6249 0.7860 -0.3329 . situacao2 0.3751 0.2140 0.3329 . regiaocentro-oeste 0.0550 0.1295 -0.3268 . regiaonordeste 0.4953 0.3175 0.3557 . regiaonorte 0.2614 0.1336 0.2908 . regiaosudeste 0.1400 0.2673 -0.3666 . regiaosul 0.0482 0.1521 -0.4848 . eCDF Mean eCDF Max distance 0.2932 0.4612 idade 0.0955 0.2400 sexo1 0.0678 0.0678 sexo2 0.0678 0.0678 raca_cor1 0.1850 0.1850 raca_cor2 0.0268 0.0268 raca_cor3 0.0004 0.0004 raca_cor4 0.1570 0.1570 raca_cor5 0.0017 0.0017 raca_cor9 0.0002 0.0002 anos_estudo 0.1297 0.2168 situacao1 0.1612 0.1612 situacao2 0.1612 0.1612 regiaocentro-oeste 0.0745 0.0745 regiaonordeste 0.1778 0.1778 regiaonorte 0.1278 0.1278 regiaosudeste 0.1272 0.1272 regiaosul 0.1039 0.1039 Summary of Balance for Matched Data: Means Treated Means Control Std. Mean Diff. Var. Ratio distance 0.1742 0.1740 0.0017 1.0091 idade 41.7223 41.8521 -0.0101 0.9239 sexo1 0.5217 0.5305 -0.0177 . sexo2 0.4783 0.4695 0.0177 . raca_cor1 0.2088 0.2036 0.0126 . raca_cor2 0.1393 0.1300 0.0269 . raca_cor3 0.0049 0.0033 0.0234 . raca_cor4 0.6384 0.6559 -0.0364 . raca_cor5 0.0070 0.0056 0.0168 . raca_cor9 0.0016 0.0016 0.0000 . anos_estudo 6.1500 6.0739 0.0184 0.9302 situacao1 0.6249 0.6407 -0.0327 . situacao2 0.3751 0.3593 0.0327 . regiaocentro-oeste 0.0550 0.0489 0.0266 . regiaonordeste 0.4953 0.4858 0.0191 . regiaonorte 0.2614 0.2740 -0.0286 . regiaosudeste 0.1400 0.1426 -0.0074 . regiaosul 0.0482 0.0487 -0.0022 . eCDF Mean eCDF Max Std. Pair Dist. distance 0.0000 0.0028 0.0018 idade 0.0047 0.0144 0.3477 sexo1 0.0089 0.0089 0.4403 sexo2 0.0089 0.0089 0.4403 raca_cor1 0.0051 0.0051 0.3142 raca_cor2 0.0093 0.0093 0.3687 raca_cor3 0.0016 0.0016 0.1169 raca_cor4 0.0175 0.0175 0.3361 raca_cor5 0.0014 0.0014 0.1510 raca_cor9 0.0000 0.0000 0.0028 anos_estudo 0.0101 0.0242 0.3693 situacao1 0.0158 0.0158 0.3706 situacao2 0.0158 0.0158 0.3706 regiaocentro-oeste 0.0061 0.0061 0.1697 regiaonordeste 0.0096 0.0096 0.3751 regiaonorte 0.0126 0.0126 0.4072 regiaosudeste 0.0026 0.0026 0.2169 regiaosul 0.0005 0.0005 0.1609 Sample Sizes: Control Treated All 53626 4292 Matched 4292 4292 Unmatched 49334 0 Discarded 0 0
- Número de Observações:
- Antes do Emparelhamento: Havia 4.292 unidades tratadas (famílias que recebem o Bolsa Família) e 53.626 unidades de controle (famílias que não recebem).
- Após o Emparelhamento: Todas as 4.292 unidades tratadas foram emparelhadas com 4.292 unidades de controle, indicando que o emparelhamento foi bem-sucedido.
Balanceamento de Covariáveis
- Antes do Matching:
- As covariáveis apresentavam diferenças consideráveis entre os grupos de tratamento e controle. Por exemplo, a média de idade era 41.7 anos para o grupo tratado e 50.5 anos para o grupo controle, com um desvio padronizado de -0.6815, indicando um grande desbalanceamento.
- A distribuição de anos de estudo e as proporções de regiões geográficas também mostravam grandes diferenças entre os grupos, evidenciando a necessidade de emparelhamento para tornar os grupos comparáveis.
- Após o Matching:
- O balanceamento das covariáveis melhorou significativamente. Por exemplo, a média de idade entre os dois grupos emparelhados era praticamente idêntica: 41.7 anos para o grupo tratado e 41.9 anos para o grupo controle, com um desvio padronizado de apenas -0.0101, indicando excelente balanceamento.
- As outras covariáveis (sexo, raça/cor, anos de estudo, e região) também apresentaram reduções drásticas nos desvios padronizados, indicando que o emparelhamento foi eficaz em tornar os grupos comparáveis.
O emparelhamento foi bem-sucedido em reduzir as diferenças iniciais entre os grupos tratados e de controle. O balanceamento das covariáveis foi alcançado com sucesso, o que sugere que o impacto do Bolsa Família pode ser comparado de maneira mais robusta entre os dois grupos, uma vez que o viés de seleção com base nas covariáveis observadas foi substancialmente reduzido.
Resultado do Efeito Médio de Tratamento
O modelo avalia o efeito médio do tratamento sobre os tratados (ATT), ou seja, o impacto do programa Bolsa Família sobre os gastos orçamentários (despesa_total).
Código
Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
-1104 147 -7.53 <0.001 44.1 -1392 -817
Term: tratamento
Type: response
Comparison: mean(1) - mean(0)
Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted Estimativa do Efeito do Tratamento
Estimativa (Estimate = -1104): A estimativa indica que, em média, as pessoas que recebem o Bolsa Família têm R$ 1.104 a menos de despesa total em comparação com aquelas que não recebem o benefício. Esse é o efeito médio do tratamento sobre os tratados (ATT), calculado como a diferença média entre os dois grupos, ajustada pelas covariáveis (idade, sexo, raça/cor, anos de estudo, situação e região).
Essa estimativa é negativa, sugerindo que o Bolsa Família não proporciona um aumento no valor gasto em despesas totais, devido ao aumento da renda ocasionado pelo programa.
p-valor < 0.001: O valor-p muito pequeno (menor que 0.001) indica que a probabilidade de essa diferença ser devida ao acaso é extremamente baixa. Portanto, podemos concluir que a diferença entre os dois grupos é estatisticamente significativa.
Conclusão
O Bolsa Família parece estar associado a uma redução significativa nos gastos orçamentários das famílias que recebem o benefício. Em média, as famílias beneficiárias do Bolsa Família gastam R$ 1.104 a menos do que as famílias não beneficiárias, com alta significância estatística e um intervalo de confiança relativamente estreito.
Colocamos como ressalvas a simplicidade dos pressupostos e especificação do modelo de Propensity Score, bem como não ser realizado comparativos de diferentes métodos de Propensity Score e Matching, portanto, o resultado encontrado neste exercício pode não ser usado com a finalidade de tomada de decisão para estudos e avaliação de impacto, mas, meramente auxilio na construção de exercícios aplicados à avaliação de impacto usando a linguagem R, usando todo o processo de coleta, análise e modelagem de dados.
Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!
Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, fale com a gente no Whatsapp e veja como fazer parte do Clube AM, clicando aqui.