Estudo de Caso: Impacto do Metro em São Paulo

O que é Pareamento? E o que significa Propensity Score? Como podemos utilizar essa ferramenta para auxiliar no estudo da avaliação de impacto? Neste post, oferecemos uma breve introdução a esse importante método da área de inferência causal, acompanhado de um estudo de caso para uma compreensão mais aprofundada de sua aplicação. Os resultados foram obtidos por meio da implementação em Python, como parte integrante do nosso curso sobre Avaliação de Políticas Públicas utilizando esta linguagem de programação.Quer saber como essa análise foi construída? Seja aluno do nosso curso Avaliação de Políticas Públicas usando Python, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em Python.

O que é Pareamento? E o que significa Propensity Score? Como podemos utilizar essa ferramenta para auxiliar no estudo da avaliação de impacto? Neste post, oferecemos uma breve introdução a esse importante método da área de inferência causal, acompanhado de um estudo de caso para uma compreensão mais aprofundada de sua aplicação. Os resultados foram obtidos por meio da implementação em Python, como parte integrante do nosso curso sobre Avaliação de Políticas Públicas utilizando esta linguagem de programação.

Pareamento

O principal benefício dos experimentos randomizados, conhecidos como RCT, reside na capacidade de tornar os grupos tratados e de controle comparáveis em proporções, tanto em características observáveis quanto não observáveis. Contudo, a implementação de um RCT não é apenas complexa, mas também dispendiosa. Além disso, quando o objetivo é avaliar uma política já implementada, a utilização de um RCT torna-se impraticável.

Em situações em que a análise visa avaliar dados já existentes, surge o desafio de garantir a semelhança entre os grupos de tratamento, não somente para evitar viés, mas também para obter grupos proporcionais. Nesses casos, torna-se imperativo empregar um método que assegure essa semelhança proporcional, conhecido como pareamento ou matching.Existem diferentes maneiras de fazer o pareamento, mas a ideia principal é usar características que podemos observar nas unidades da amostra para encontrar unidades não tratadas que se parecem com aquelas que receberam tratamento.

Em outras palavras, tentamos garantir que, para cada unidade tratada, haja uma ou mais unidade semelhantes no grupo de controle.

Quando o pareamento é feito corretamente, criamos uma nova amostra onde o tratamento não está relacionado às características observáveis. Isso significa que, ao comparar os resultados entre o grupo que recebeu tratamento e o grupo de controle, não somos influenciados pelas diferenças nas variáveis que podemos ver.A importância do equilíbrio das características entre os grupos é que ele permite maior robustez para a escolha do modelo usado para estimar o efeito do tratamento.Em amostras perfeitamente balanceadas, o efeito do tratamento pode ser obtido por uma simples diferença nas médias, tal qual um experimento. Entretanto, a maior dificuldade é garantir que não hajam motivos para um desbalanceamento nas variáveis não observáveis. Por isso, é preciso parear utilizando o maior número de variáveis relevantes.

Quer saber como essa análise foi construída? Seja aluno do nosso curso Avaliação de Políticas Públicas usando Python, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em Python.

Como exemplo para mostrar o poder dos métodos de pareamento utilizaremos o caso do impacto econômico do metrô de São Paulo. O transporte pode ter grande impacto nos aspectos econômicos de uma localidade, pois permite e expande o acesso das pessoas aos empregos, promove a eficiência e fomenta economias de aglomeração. Assim, estimaremos o impacto da construção de estações de metrô na verticalização, medida pela proporção de domicílios que são apartamentos, dos domicílios próximos a elas. Mais especificamente, analisaremos o impacto das estações de metrô construídas em São Paulo entre 2002 e 2007, das linhas verdes e lilás.

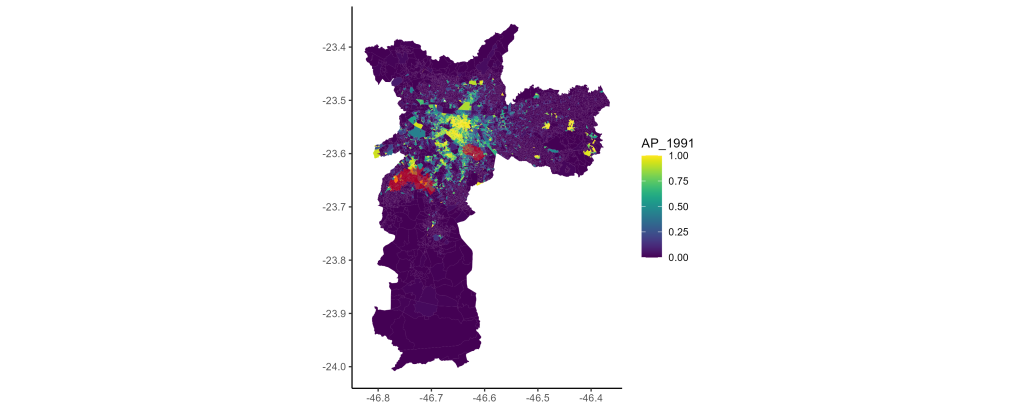
Utilizaremos dados dos censos de 1991, 2000 e 2010 com algumas variáveis em nível de setor censitário para a cidade de São Paulo. Para fins de definição dos setores censitários tratados, ou seja, que sofreram a intervenção da política pública, estamos considerando a distância de até 1km até a estação construída mais próxima. No mapa a seguir, mostramos como era a verticalização dos setores censitários de São Paulo em 1991.

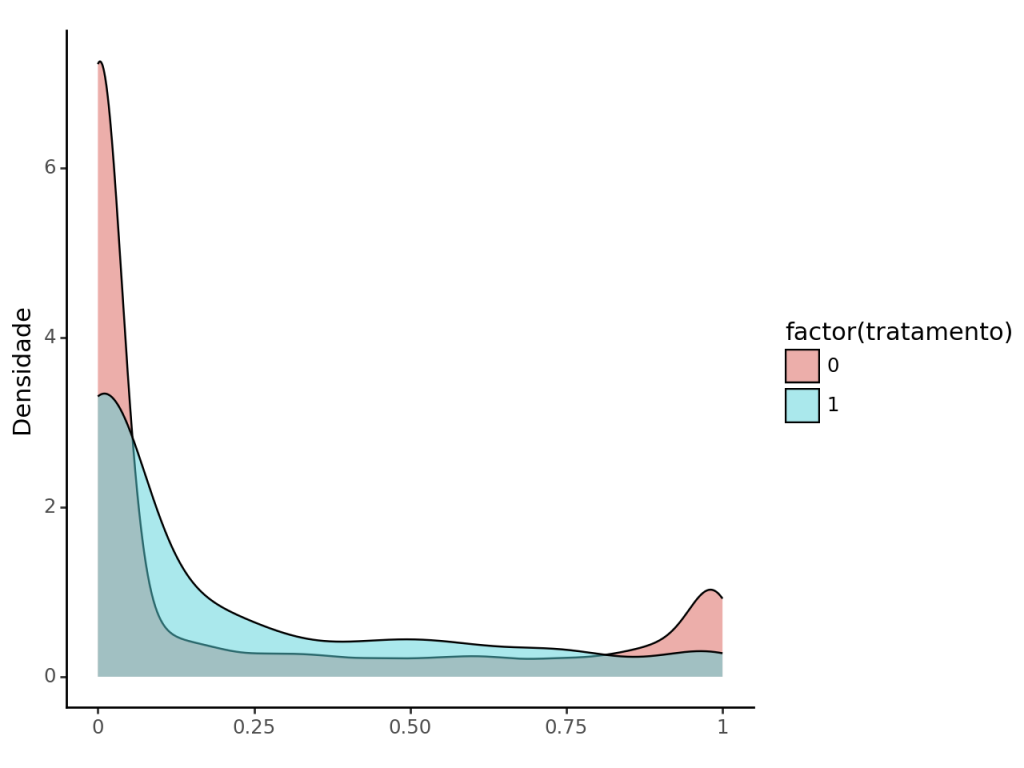
Quando comparamos a distribuição da verticalização entre estes dois grupos (tratados (1) e restantes (0)) isso fica mais claro.

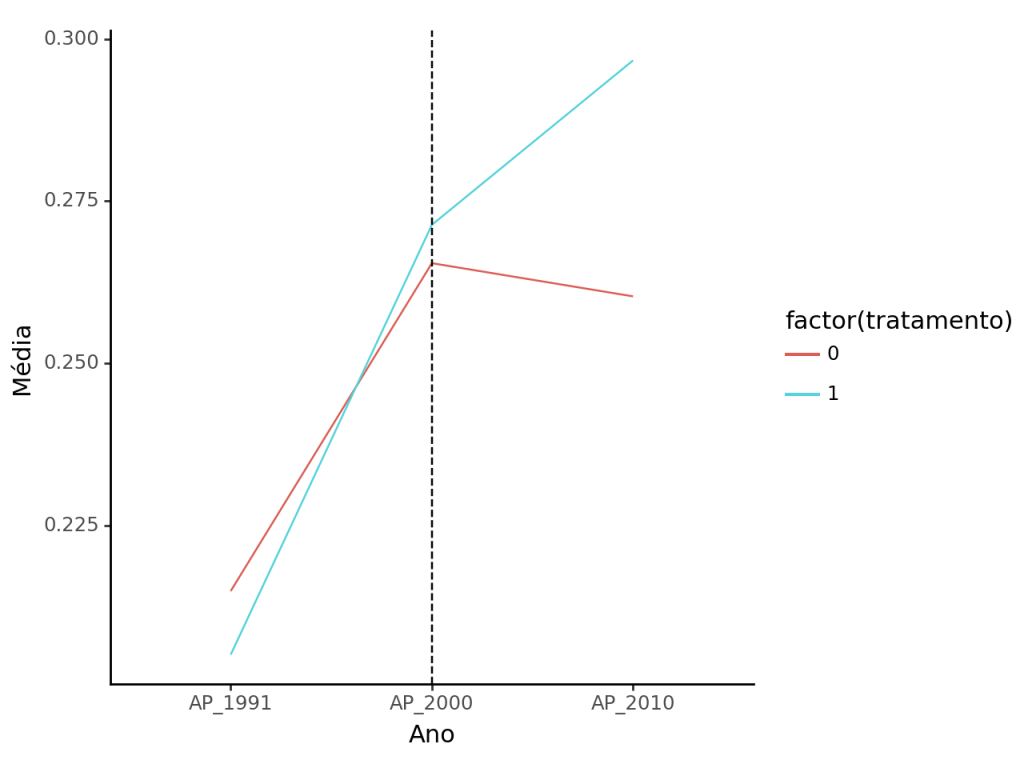
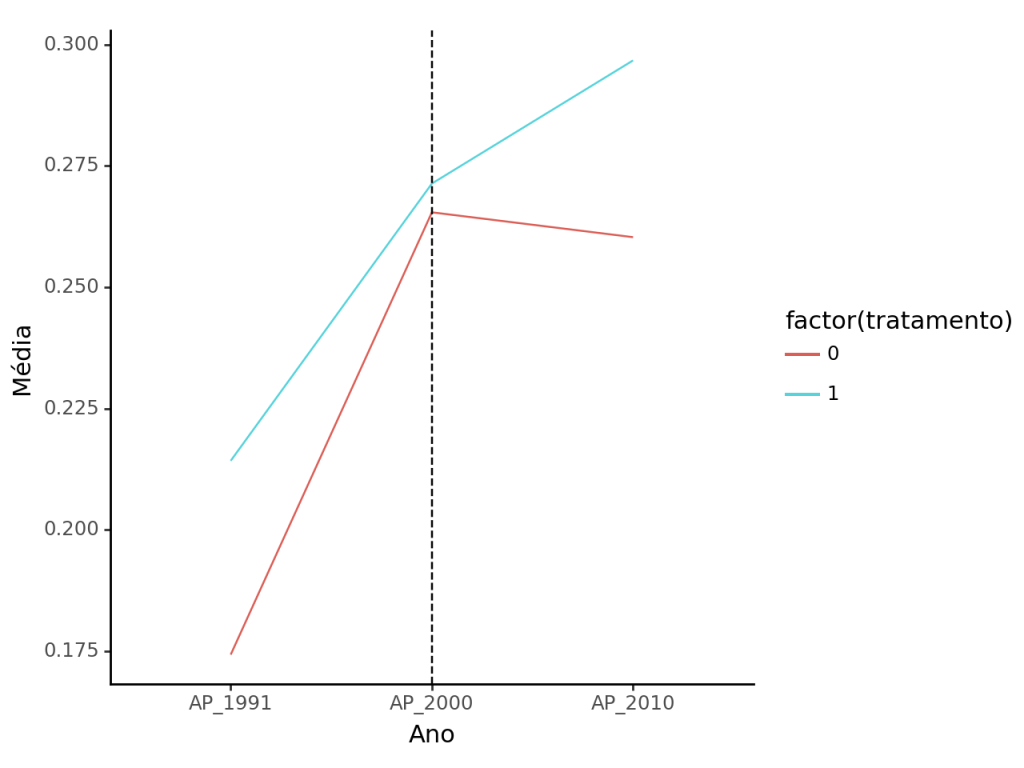
Veja que se formos estimar o modelo de diferenças-em-diferenças, nós precisamos adequar o grupo de controle para que as tendências fiquem paralelas.

Assim, para avaliar o efeito, é preciso tornar esses grupos semelhantes. Para isso, utilizaremos o pareamento, que permite selecionar setores de dentro do grupo restante para formar um grupo de controle parecido com o grupo de tratamento. Vamos empregar o método de pareamento por vizinhos mais próximos.

Além da variável de verticalização, também utilizamos a renda domiciliar per capita, a proporção de pessoas com ensino superior, a proporção de domicílios que são alugados e a proporção de jovens adultos (25-34 anos) entre os moradores do setor censitário.

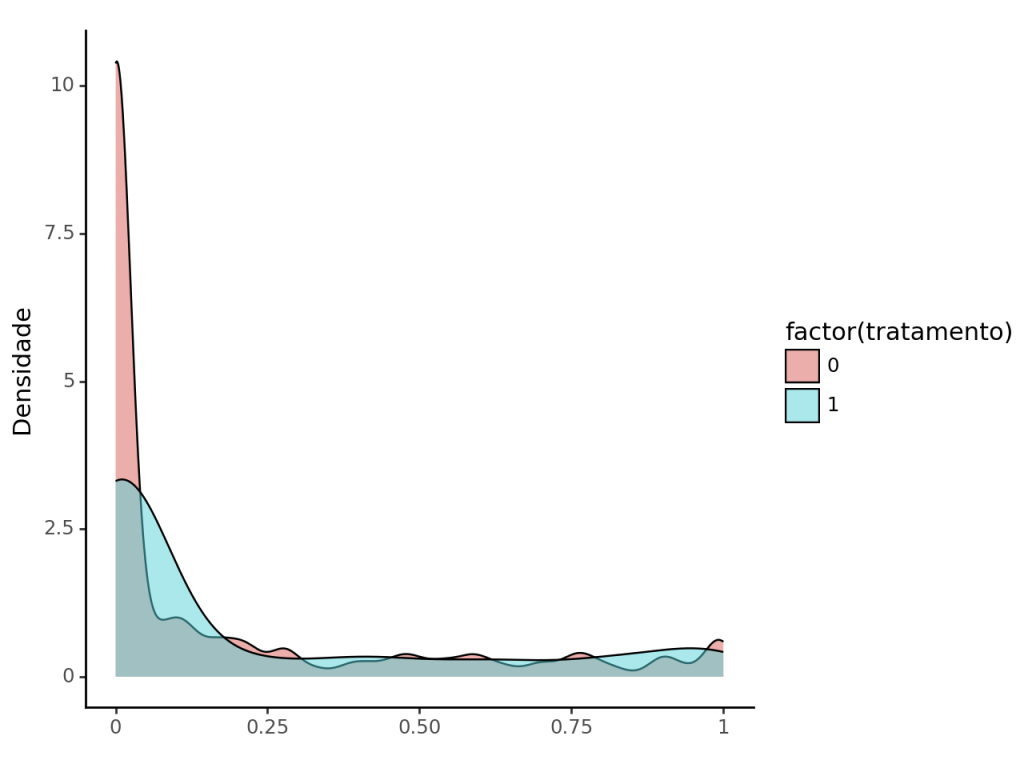
Após o uso do pareamento, aparentemente não tivemos sucesso em tornar parecidas as distribuições.

Muito menos conseguimos melhorar as tendências.

O método de pareamento, portanto, é inútil? Claramente não podemos afirmar isso, afinal, como qualquer método, existe diferentes formas de realizar a sua aplicação, visto que há diversos modelos/algoritmos que podem ser empregados.

Propensity Score

Uma forma interessante de obtenção da distância entre as observações é o Propensity Score, que considera a probabilidade da observação pertencem ao grupo de controle ou tratamento, independente de seu pertencimento "original". Para tanto, criamos um escore de propensity (a probabilidade de pertencimento de determinado grupo) usando uma regressão logística e tomando como variável dependente a variável binária que representa o tratamento, e como variáveis preditoras as características das unidades.

Após a estimação do escore de propensão, devemos realizar o match (pareamento das unidades conforme o escore). Aqui, aplicamos o emparelhamento de 1:1 (one-to-one Matching).

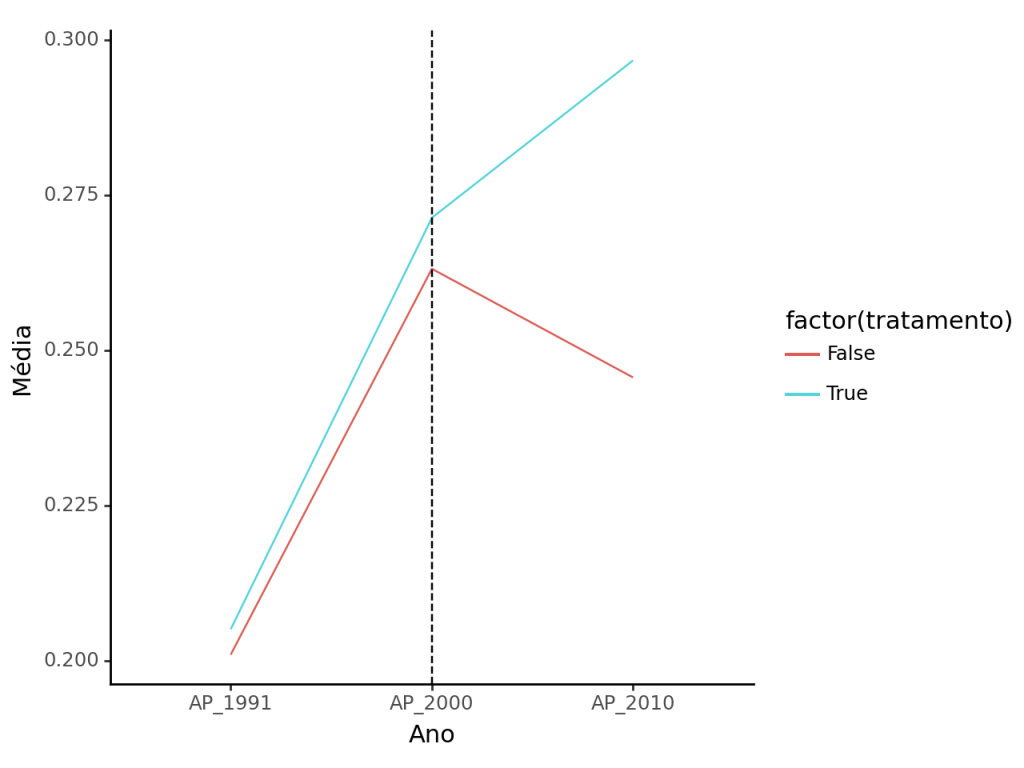Neste método, cada unidade no grupo de tratamento é emparelhado com exatamente um unidade no grupo de controle que tem o escore de propensão mais próximo. Isso garante um emparelhamento direto entre os indivíduos e seus controles mais próximos em termos de probabilidade de tratamento.Com isso, teremos uma nova forma das tendências paralelas conforme a figura abaixo:

Bem melhor que antes, certo?

Referências

Facure, Matheus. 2022. Causal Inference for The Brave and True. https://matheusfacure.github.io/python-causality-handbook/landing-page.html.

Stuart, Elizabeth A. 2010. «Matching methods for causal inference: A review and a look forward». Statistical science: a review journal of the Institute of Mathematical Statistics 25 (1): 1.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Criando um Dashboard de análise de Ações no Python

Analisando séries temporais no Python e esquecendo de vez o Excel

Cálculo do Retorno Econômico de uma Política Pública

Simplificando análises de dados manuais do Excel usando o Python

Outros artigos relacionados

Deploy de modelos com Python + Shinylive + GitHub gastando ZERO reais

Colocar modelos em produção pode ser um grande desafio. Lidar com custos monetários, infraestrutura operacional e complexidades de códigos e ferramentas pode acabar matando potenciais projetos. Uma solução que elimina todos estes obstáculos é a recém lançada Shinylive. Neste artigo mostramos um exemplo com um modelo de previsão para o preço do petróleo Brent.

Como automatizar tarefas repetitivas usando Python? Um exemplo para largar o Excel

Manter relatórios diários com dados e análises atualizados é um desafio, pois envolve várias etapas: coleta de dados, tratamento de informações, produção de análises e atualização de relatório. Para superar este desafio algumas ferramentas como Python + Quarto + GitHub podem ser usadas para automatizar tudo que for automatizável. Neste artigo mostramos um exemplo com dados do mercado financeiro.

Criando um Dashboard de análise de Ações no Python

Um Dashboard é um painel de controle que consolida uma variedade de informações sobre um determinado objeto de estudo em um ou mais painéis. Ele simplifica significativamente o processo de análise de dados, oferecendo uma visão global e fácil de entender. Uma maneira simples de construir um Dashboard para acompanhar uma ação específica é utilizando duas ferramentas: Quarto e Python. Neste post, mostramos o resultado da criação de um Dashboard de Ação.