Diversos métodos econométricos têm como principal finalidade melhorar o processo de investigar o efeito de uma variável sobre a outra, e um importante método encontra-se no uso de Variáveis Instrumentais na análise de regressão linear. Mas como podemos utilizar essa ferramenta para auxiliar no estudo da avaliação de impacto?

Neste post, oferecemos uma breve introdução a esse importante método da área de inferência causal, acompanhado de um estudo de caso para uma compreensão mais aprofundada de sua aplicação. Os resultados foram obtidos por meio da implementação em R, como parte integrante do nosso curso sobre Avaliação de Políticas Públicas utilizando esta linguagem de programação.

Variáveis Instrumentais

As variáveis instrumentais (VI), é um método presente no arcabouço econométrico e estatístico, que oferece uma abordagem para lidar com problemas de endogeneidade e viés de variáveis omitidas em modelos de regressão. Quando variáveis independentes estão correlacionadas com o erro de um modelo de regressão, os estimadores de mínimos quadrados ordinários (MQO) se tornam enviesados e inconsistentes, invalidando as inferências estatísticas.

As variáveis instrumentais ajudam a superar esses desafios introduzindo variáveis adicionais, chamadas instrumentos, que estão correlacionadas com as variáveis independentes problemáticas, mas não com o erro do modelo. Essencialmente, os instrumentos servem como proxies confiáveis para as variáveis endógenas, permitindo a obtenção de estimativas consistentes dos parâmetros do modelo.

Uma forma comum de introduzir VI é através do método dos mínimos quadrados em dois estágios (MQ2E ou 2SLS). Neste método, no primeiro estágio, as VI são utilizadas para estimar a variável endógena. No segundo estágio, a variável endógena estimada é então usada como variável independente no modelo de interesse. Isso ajuda a resolver o problema de endogeneidade, permitindo estimativas consistentes dos parâmetros de interesse.

Equação de cálculo do método dos mínimos quadrados em dois estágios:

Seja o modelo de regressão original:

Onde:
- é a variável dependente.
- é a matriz de variáveis independentes, incluindo tanto variáveis endógenas quanto exógenas.
- é o vetor de parâmetros.
- é o termo de erro aleatório.

Suponha que contenha variáveis endógenas que são correlacionadas com . Para lidar com isso, vamos introduzir variáveis instrumentais , onde é um conjunto de variáveis que são correlacionadas com as variáveis endógenas, mas não com o erro .

No primeiro estágio do MQ2E, estimamos a variável endógena utilizando as variáveis instrumentais . Isso nos dá a variável instrumental estimada .

No segundo estágio, substituímos por na equação original e estimamos o modelo final usando a equação:

Onde é o novo termo de erro, que agora deve estar não correlacionado com . Isso nos permite estimar os parâmetros de interesse de forma consistente, mesmo em presença de endogeneidade.

Qual o impacto do gasto de segurança no crime?

Quer saber como essa análise foi construída? Seja aluno do nosso curso Avaliação de Políticas Públicas usando R, e tenha acesso às aulas teóricas e práticas, com o código disponibilizado em Python.

Alguns instrumentos foram propostos ao longo do tempo para esse tipo de problema, sendo o mais famoso o uso de ciclos eleitorais (Levitt 1995).

A lógica pra utilização dessa variável é que gestores costumam aumentar a contratação de profissionais de segurança em períodos de véspera de eleição. Uma possível crítica a esse instrumento é que outras despesas também crescem nessa época e podem afetar o nível de crimes, como em educação, empregos e gastos sociais.

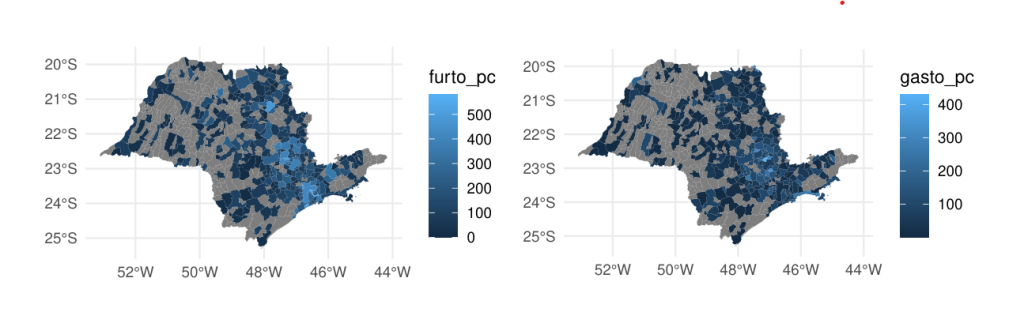
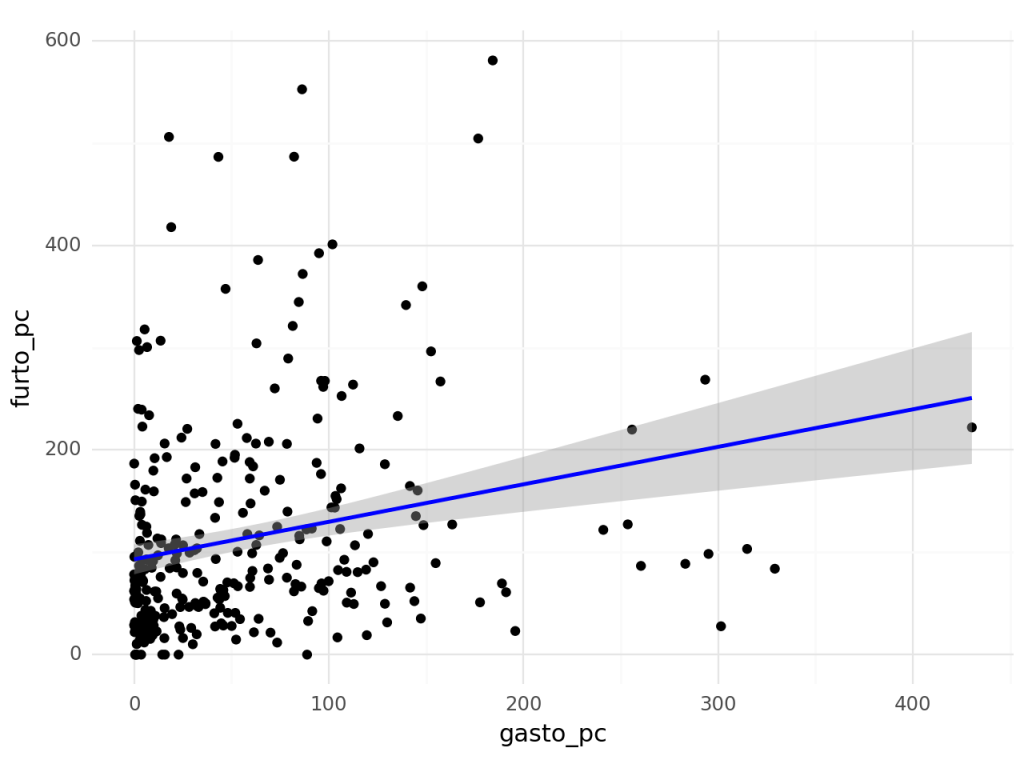
Para replicarmos esse problema, iremos estimar o efeito dos gastos em segurança pública (Finbra) nos dados de furtos de veículo (SSP) nos municípios de São Paulo de 2013 a 2019.

Para evitar complicações adicionais de estimar um modelo de painel, pré-selecionamos aleatoriamente um ano para cada município. A variável de furtos está disposta em número a cada 100.000 habitantes. Já a despesa com segurança está medida per capita. A nossa variável de ciclo eleitoral é uma variável binária que retorna 1, em caso de ano eleitoral ou pré-eleitoral e 0, caso contrário.

===============================================
                              OLS          2SLS
-----------------------------------------------
Dep. Variable            furto_pc      furto_pc
Estimator                     OLS       IV-2SLS
No. Observations              313           313
Cov. Est.                  robust        robust
R-squared                  0.0549       -3.0659
Adj. R-squared             0.0519       -3.0790
F-statistic                14.906        1.6454
P-value (F-stat)           0.0001        0.1996
==================     ==========   ===========
Intercept                  93.162        247.66
                         (14.334)      (2.3783)
gasto_pc                   0.3664       -2.3950
                         (3.8608)     (-1.2827)
==================== ============ =============
Instruments                             eleicao
-----------------------------------------------

T-stats reported in parentheses