No mês de dezembro, iremos lançar uma nova versão do Clube do Código. O projeto de compartilhamento de códigos da Análise Macro vai avançar para uma versão 2.0, que incluirá a existência de uma comunidade no Telegram/Whatsapp, de modo a reunir os membros do Novo Clube, compartilhando com eles todos os códigos dos nossos posts feitos aqui no Blog, exercícios de análise de dados de maior fôlego, bem como tirar dúvidas sobre todos os nossos projetos e Cursos Aplicados de R.
Para ilustrar o que vamos compartilhar lá nesse novo ambiente, estou publicando nesse espaço alguns dos nossos exercícios de análise de dados. Esses exercícios fazem parte do repositório atual do Clube, que irá migrar para o novo projeto. Além de todos os exercícios existentes, vamos adicionar novos exercícios e códigos toda semana, mantendo os membros atualizados sobre o que há de mais avançado em análise de dados, econometria, machine learning, forecasting e R.
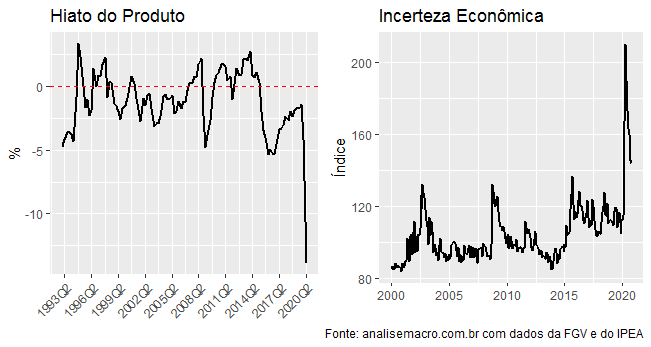
Hoje, vou mostrar um exercício que fizemos no Clube que buscava capturar o efeito da incerteza sobre o nível de atividade. A motivação para o exercício é, claro, o aumento da incerteza econômica como fruto da pandemia que estamos vivendo. Os gráficos a seguir ilustram o comportamento do hiato do produto (diferença entre o produto potencial e o produto efetivo) e da incerteza econômica. A primeira é uma série produzida pelo IPEA e a segunda é um índice fornecido pela FGV.
O aumento da incerteza tem efeitos diversos sobre o organismo econômico, como a redução do consumo pelas famílias e do investimento pelas empresas. Podemos, por suposto, capturar o seu efeito sobre o nível de atividade, de forma geral, estimando uma Curva IS que adiciona esse componente de incerteza, como na equação abaixo:
(1)
Basicamente, a Curva IS estimada irá descrever a dinâmica do hiato do produto com base em **suas próprias defasagens**, da **taxa de juros real**, da **variação do superávit primário** e de um **índice de incerteza econômica**. A tabela abaixo resume a estimação dessa Curva considerando o método de mínimos quadrados como benchmark e os métodos TSLS e GMM como referências mais robustas para o exercício.
| Variável Dependente: Hiato do Produto | |||
| OLS | TSLS | GMM | |
| (1) | (2) | (3) | |
| Intercepto | 6.17*** (1.37) | 12.01*** (3.74) | 17.35*** (2.81) |
| Hiato (-1) | 0.70*** (0.06) | 0.56*** (0.09) | 0.47*** (0.08) |
| Juro Real | -0.07* (0.04) | -0.17*** (0.06) | -0.25*** (0.04) |
| Variação do SPrimário | -0.71* (0.36) | -0.10 (0.97) | 1.03 (0.85) |
| Incerteza | -0.06*** (0.01) | -0.11*** (0.03) | -0.16*** (0.03) |
| J-Test | 5.95 | ||
| J-Test (p-valor) | 0.43 | ||
| Observations | 70 | 67 | 67 |
| R2 | 0.86 | 0.89 | |
| Adjusted R2 | 0.85 | 0.89 | |
| Residual Std. Error | 0.84 (df = 65) | 0.74 (df = 62) | |
| F Statistic | 99.99*** (df = 4; 65) | 121.38*** (df = 4; 62) | |
| Nota: | *p<0.1; **p<0.05; ***p<0.01 | ||
Os resultados preliminares encontrados sugerem que existe um efeito negativo da incerteza sobre o hiato do produto. Isto é, mais incerteza afeta as decisões de consumo e investimento, que fazem com que o PIB da economia seja menor, reduzindo assim o hiato do produto.
Com base nesses resultados, é possível verificar que a "estabilização" da incerteza em patamares elevados tem efeitos negativos sobre a recuperação do nível de atividade.
______________________
(*) Cadastre-se aqui na nossa Lista VIP para receber um super desconto na abertura das Turmas 2021.