Previsão de séries temporais em escala é um tópico cada vez mais necessário no mundo atual, já que o tempo é um recurso limitado e a quantidade de séries à estimar é crescente. Neste contexto, demonstramos o uso do framework tidyverts para estimar diferentes modelos de previsão para múltiplas séries temporais no R, sem muito esforço ou repetição de código.
De forma concreta, demonstraremos a estimação de dois modelos univariados (ARIMA e ETS) para previsão da variável correspondente a produtividade total dos fatores para um total de 9 países selecionados do dataset Penn World Table 10.0. O exercício é bastante simples, com a finalidade apenas de exemplificar a utilização do framework quando temos múltiplas séries para estimar. Dessa forma, não nos preocupamos aqui com questões relacionadas à especificação dos modelos em si, mesmo que estas configuram etapas de extrema importância no processo de modelagem.
Pacotes
O tidyverts é uma família de pacotes focada em séries temporais com a filosofia do tidyverse, ou seja, a união do melhor dos dois mundos. Dessa forma, neste exercício vamos usar o pacote tsibble para converter nosso objeto de séries temporais em formato tidy. Já para estimar e prever os modelos usamos os pacotes fable e fabletools, que oferecem as funções ARIMA() e ETS(). E os dados utilizados são provenientes do pacote pwt10.
# Instalar/carregar pacotes
if(!require("pacman")) install.packages("pacman")
pacman::p_load(
"pwt10",
"fable",
"fabletools",
"tsibble",
"magrittr",
"dplyr",
"tidyr",
"ggplot2",
"ggthemes"
)
Dados
O dataset pwt10.0 contém diversas variáveis das contas nacionais e outros indicadores de diversos países em frequência anual. Aqui utilizaremos a série correspondente à produtividade total dos fatores (a valores nacionais constantes, 2017 = 1) para uma seleção de 9 países. Selecionamos as colunas de interesse e também os países, assim como removemos as observações ausentes. Por fim, transformamos o data.frame para a classe tsibble utilizando a função as_tsibble(). Isso é necessário para realizar as estimações dos modelos com este framework e é o segredo para fazermos a modelagem e previsão para todos os países de uma única vez. O objeto terá uma key que identifica cada país nesse conjunto de dados e um index que expressa a frequência da série de tempo. Importante: caso os dados fossem mensais, precisaríamos antes tratar a coluna de datas usando a função tsibble::yearmonth().
tfp <- pwt10::pwt10.0 %>% dplyr::select(country, year, rtfpna) %>% dplyr::filter( country %in% c( "Argentina", "Brazil", "Canada", "Chile", "Mexico", "Peru", "Turkey", "United States of America", "Uruguay" ) ) %>% tidyr::drop_na() %>% tsibble::as_tsibble(key = country, index = year) tfp # A tsibble: 594 x 3 [1Y] # Key: country [9] country year rtfpna <fct> <int> <dbl> 1 Argentina 1954 1.13 2 Argentina 1955 1.16 3 Argentina 1956 1.14 4 Argentina 1957 1.14 5 Argentina 1958 1.17 6 Argentina 1959 1.08 7 Argentina 1960 1.13 8 Argentina 1961 1.11 9 Argentina 1962 1.07 10 Argentina 1963 1.01 # ... with 584 more rows
Estimar modelos
Com os dados prontos, podemos realizar as estimações e previsões dessas variáveis. Os modelos simples que utilizaremos neste exercício serão armazenados em um objeto de classe mable, que é uma estrutura tabular de armazenamento das informações dos modelos estimados. Para isso, colocamos dentro da função model() todas as especificações de modelos que serão estimados. A única restrição é que todos os modelos devem ter em comum uma mesma variável dependente. Para os modelos em si utilizamos o pacote fable que oferece diversos algoritmos para estimação automatizada de alguns modelos.
model_fit <- tfp %>% fabletools::model( arima = fable::ARIMA(rtfpna), ets = fable::ETS(rtfpna) ) model_fit # A mable: 9 x 3 # Key: country [9] country arima ets <fct> <model> <model> 1 Argentina <ARIMA(0,1,0)> <ETS(A,N,N)> 2 Brazil <ARIMA(0,2,1)> <ETS(M,A,N)> 3 Canada <ARIMA(0,2,1)> <ETS(A,Ad,N)> 4 Chile <ARIMA(2,0,0) w/ mean> <ETS(A,N,N)> 5 Mexico <ARIMA(0,1,0)> <ETS(M,N,N)> 6 Peru <ARIMA(0,1,1)> <ETS(M,N,N)> 7 Turkey <ARIMA(0,1,0)> <ETS(M,N,N)> 8 Uruguay <ARIMA(1,1,0)> <ETS(A,Ad,N)> 9 United States of America <ARIMA(0,1,0) w/ drift> <ETS(A,A,N)>
Previsões
Por fim, as previsões podem ser feitas sobre um objeto com dados de teste ou sobre um determinado horizonte. Neste exercício optamos por não separar amostras de treino e teste, dado número baixo de observações, portanto realizamos as previsões com o objeto anterior para um horizonte de 10 anos fora da amostra usando a função forecast().
model_frcst <- model_fit %>% fabletools::forecast(h = 10) model_frcst # A fable: 180 x 5 [1Y] # Key: country, .model [18] country .model year rtfpna .mean <fct> <chr> <dbl> <dist> <dbl> 1 Argentina arima 2020 N(0.93, 0.0017) 0.932 2 Argentina arima 2021 N(0.93, 0.0033) 0.932 3 Argentina arima 2022 N(0.93, 0.005) 0.932 4 Argentina arima 2023 N(0.93, 0.0067) 0.932 5 Argentina arima 2024 N(0.93, 0.0084) 0.932 6 Argentina arima 2025 N(0.93, 0.01) 0.932 7 Argentina arima 2026 N(0.93, 0.012) 0.932 8 Argentina arima 2027 N(0.93, 0.013) 0.932 9 Argentina arima 2028 N(0.93, 0.015) 0.932 10 Argentina arima 2029 N(0.93, 0.017) 0.932 # ... with 170 more rows
Resultados
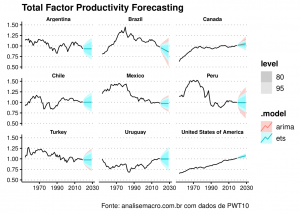
Com estes simples passos já temos tudo que precisamos para avaliar os resultados, ou seja, verificar a acurácia, investigar e diagnosticar os resíduos, visualizar a previsão, etc. Nesta oportunidade vamos apenas visualizar graficamente o resultado, plotando os dados observados por cada país e as previsões de cada um dos dois modelos. Isso pode ser feito de forma muito fácil apenas utilizando os dados do objeto com as previsões (model_frcst) e os dados com os valores observados (tfp) na função autoplot().
model_frcst %>% fabletools::autoplot(tfp) + ggplot2::facet_wrap(~country, ncol = 3) + ggplot2::labs( title = "Total Factor Productivity Forecasting", y = "", x = "" )
Referências úteis
Recomendamos a leitura do Forecasting: Principles and Practice de Hyndman, R.J., & Athanasopoulos, G. para se aprofundar na utilização desse framework, que oferece uma série de utilidades para as tarefas de modelagem e previsão com uma abordagem moderna e intuitiva.